csa Round #70

Digit Holes

Time limit: 1000 ms
Memory limit: 256 MB

 

When writing digits, some of them are considered to have holes: 00, 66 and 99 have one hole, while 88 has two holes. The other digits don't have any holes.

Given two integers AA and BB, find a value in the interval [A, B][A,B] that has the maximum total number of holes in its digits. If the solution is not unique, print the smallest one.

Standard input

The first line contains two integers AA and BB.

Standard output

Print the answer on the first line.

Constraints and notes

• 0 \leq A \leq B \leq 10000≤A≤B≤1000

Input	Output	Explanation
0 20	8	88 is the first integer in [0, 20][0,20] with 22 holes.
10 20	18	1818 is the only integer in [10, 20][10,20] with 22 holes.
1 100	88	8888 is the only integer in [1, 100][1,100] with 44 holes.

统计每一位的贡献，直接取就行了，我本来还想去sort，那样麻烦了蛮多

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
vector<pii>A;
int la(int t)
{
    int ans=;
    if(!t)ans=;
    while(t)
    {
        if(t%==||t%==||t%==)
            ans+=;
        else if(t%==)
            ans+=;
        t/=;
    }
    return ans;
}
int main()
{
    int a,b;
    cin>>a>>b;
    int ma=a,maf=;
    for(int i=a; i<=b; i++)
        if(la(i)>maf)
        {
            ma=i;
            maf=la(i);
        }
    cout<<ma;
    return ;
}

Right Down Path

Time limit: 1000 ms
Memory limit: 256 MB

 

You are given a binary matrix AA of size N \times MN×M. You should find a path that starts in a cell, then goes to the right at least one cell, then goes down at least one other cell. That path should contain only cells equal to 11.

Find the longest path respecting these constraints.

Standard input

The first line contains two integers NN and MM.

Each of the next NN lines contains MM integers, 00 or 11, representing the elements of matrix AA.

Standard output

Print the size of the longest path on the first line.

Constraints and notes

• 2 \leq N, M \leq 3002≤N,M≤300
• It is guaranteed there is always at least one valid path

Input	Output	Explanation
4 4 0 1 1 0 1 1 1 0 1 0 1 0 1 1 0 0	4	One of the solutions of length 44 is bolded below. 0\ \bold{1}\ \bold{1}\ 00 1 1 0 1\ 1\ \bold{1}\ 01 1 1 0 1\ 0\ \bold{1}\ 01 0 1 0 1\ 1\ 0\ 01 1 0 0
5 4 1 0 1 0 1 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1	5	The solutions of length 55 is bolded below. 1\ 0\ 1\ 01 0 1 0 \bold{1}\ \bold{1}\ \bold{1}\ 11 1 1 1 1\ 0\ \bold{1}\ 01 0 1 0 1\ 0\ \bold{1}\ 11 0 1 1 0\ 0\ 0\ 10 0 0 1
5 5 0 0 0 0 1 1 1 0 0 1 0 1 0 1 1 0 0 0 0 1 1 1 1 1 1	4	Note that you need to move at least once right and down. Because of this, the solutions consisting of the 5 ones on the sides is not valid. The valid solution is bolded below. 0\ 0\ 0\ 0\ 10 0 0 0 1 1\ 1\ 0\ 0\ 11 1 0 0 1 0\ 1\ 0\ \bold{1}\ \bold{1}0 1 0 1 1 0\ 0\ 0\ 0\ \bold{1}0 0 0 0 1 1\ 1\ 1\ 1\ \bold{1}1 1 1 1 1

从一个点开始可以向右然后向下，但是必须要走一格的，所以暴力的时候要判断有没有路

n^3的暴力

#include<bits/stdc++.h>
using namespace std;
int a[][];
int main()
{
    int n,m,ans=;
    cin>>n>>m;
    for(int i=; i<n; i++)
        for(int j=; j<m; j++)
            cin>>a[i][j];
    for(int i=; i<n-; i++)
        for(int j=,k; j<m-; j++)
        {
            if(a[i][j])
            {
                for(k=j+; k<m; k++)
                {
                    if(a[i][k])
                    {
                        if(a[i+][k])
                        {
                            int t=k-j+;
                            for(int l=i+;l<n;l++)
                            if(a[l][k])t++;
                            else break;
                            ans=max(ans,t);
                        }
                    }
                    else break;
                }
                j=k;
            }
        }
    cout<<ans;
    return ;
}

但是我当时写的是用后缀和和优化的，其实完全没有必要

#include<bits/stdc++.h>
using namespace std;
int a[][],s[][];
int main()
{
    int n,m,ans=;
    cin>>n>>m;
    for(int i=; i<n; i++)
        for(int j=; j<m; j++)
            cin>>a[i][j];
    for(int i=n-; i>=; i--)
        for(int j=; j<m; j++)
            if(a[i][j])s[i][j]=s[i+][j]+;
    for(int i=; i<n; i++)
        for(int j=; j<m; j++)
        {
            if(a[i][j])
            for(int k=j; k<m; k++)
            {
                if(a[i][k])ans=max(ans,k-j+s[i][k]);
                else break;
            }
        }
        cout<<ans;
    return ;
}

Min Distances

Time limit: 1000 ms
Memory limit: 256 MB

 

You should build a simple, connected, undirected, weighted graph with NN nodes. You are given MM constraints of the type a, b, ca,b,c, representing the fact that the minimum distance between nodes aa and bb should be cc.

Standard input

The first line contains two integers NN and MM.

Each of the next MM lines contains three integers aa, bb and cc representing a constraint.

Standard output

If there is no solution output -1−1.

Otherwise, print the number of edges your graph has on the first line.

Each of the next line should contain three integers aa, bb, ww, representing an edge (a, b)(a,b)with weight ww.

Constraints and notes

• 2 \leq N \leq 1002≤N≤100
• 0 \leq M \leq \binom{N}{2}0≤M≤(​2​N​​)
• 1 \leq a, b \leq N1≤a,b≤N and a \neq ba≠b
• 1 \leq c \leq 10^61≤c≤10​6​​
• The weigths ww should respect 1 \leq w \leq 10^71≤w≤10​7​​

Input	Output	Explanation
3 3 1 2 1 2 3 2 1 3 3	2 1 2 1 2 3 2	Note that the graph is not unique 12123
5 4 3 1 2 3 5 2 1 5 3 4 2 2	6 1 3 2 5 1 3 2 4 2 2 5 4 3 5 2 5 4 1	Note that the graph is not unique 23242112354
3 3 1 2 1 2 3 1 3 1 3	-1	There's no graph to satisfy all 3 restrictions.

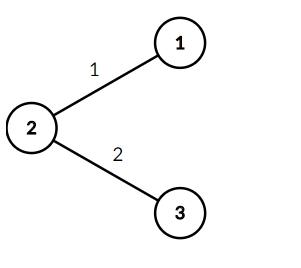
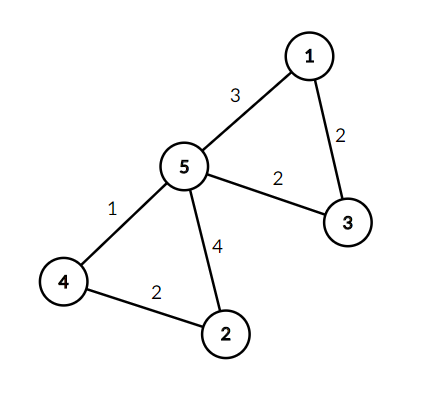
给定n个点M条边的最短路，让你构造一个图满足这个

因为是多源最短路，点数也不多，所以直接Floyd走一波然后判断是否合法

因为是无向图所以直接输出一半就好了

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int M[][];
struct T
{
    int a,b,c;
} t;
vector<T>V;
int main()
{
    memset(M,INF,sizeof M);
    int n,m;
    cin>>n>>m;
    for(int i=; i<m; i++)
        cin>>t.a>>t.b>>t.c,V.push_back(t),M[t.a][t.b]=t.c,M[t.b][t.a]=t.c;
    for(int k=; k<=n; k++)
        for(int i=; i<=n; i++)
            for(int j=; j<=n; j++)
                M[i][j]=min(M[i][j],M[i][k]+M[k][j]);
    int f=;
    for(int i=; i<m&&f; i++)
    {
        t=V[i];
        if(M[t.a][t.b]!=t.c)f=;
    }
    if(!f)printf("-1");
    else
    {
        printf("%d\n",n*(n-)/);
        for(int i=; i<=n; i++)
            for(int j=i+; j<=n; j++)
                if(M[i][j]!=INF)
                    printf("%d %d %d\n",i,j,M[i][j]);
                else printf("%d %d %d\n",i,j,(int)1e7);
    }
    return ;
}

Distribute Candies

Time limit: 1000 ms
Memory limit: 256 MB

 

You should distribute NN candies in KK boxes such that the difference between the maximum and the minimum number of candies in a box is minimized. In addition, every pair of consecutive boxes should have a different number of candies.

Standard input

The first line contains two integers NN and KK.

Standard output

If there is no solution output -1−1.

Otherwise, print KK numbers on the first line, representing the number of candies in each box.

Constraints and notes

• 1 \leq N \leq 10^{18}1≤N≤10​18​​
• 1 \leq K \leq 10^51≤K≤10​5​​
• Each box has to have a strictly positive amount of candies
• If the solution is not unique you can print any of them

Input	Output
15 2	8 7
16 4	3 5 3 5
100 80	-1

把n个盒子放进和为m的盒子里，且相邻盒子放的数不一样

取中间值，然后去构造就行了，奇偶分析

#include<bits/stdc++.h>
using namespace std;
const int  N=1e5+;
typedef long long ll;
ll n,m,a[N];
int main()
{
    cin>>m>>n;
    if(n==)cout<<m;
    else
    {
        m-=n;
        if(m<n/)cout<<-;
        else
        {
            ll k=m%n;
            if(k<(n/))k+=n;
            m-=k,m+=n,m/=n;
            for(int i=; i<n; i++)a[i]=m;
            if(k==(n/))
            {
                for(int i=; i<n; i+=)a[i]++;
            }
            else if(k==((n+)/))
            {
                for(int i=; i<n; i+=)a[i]++;
            }
            else
            {
                for(int i=; i<n; i+=)a[i]++,k--;
                for(int i=; k>&&i<n; i+=)a[i]++,k--;
                for(int i=; k>&&i<n; i+=)a[i]++,k--;
            }
            for(int i=; i<n; i++)cout<<a[i]<<" ";
        }
    }
    return ;
}

Squared Ends

Time limit: 2000 ms
Memory limit: 256 MB

 

You are given an array AA of NN integers. The cost of a subarray [A_l, A_{l+1},...A_r][A​l​​,A​l+1​​,...A​r​​]is equal to (A_l -A_r)^2(A​l​​−A​r​​)​2​​. Partition the array in KK subarrays having a minimum total cost.

Standard input

The first line contains two integers NN and KK.

The second line contains NN integers representing the elements of AA.

Standard output

Print the minimum total cost on the first line.

Constraints and notes

• 1 \leq N \leq 10^41≤N≤10​4​​
• 1 \leq K \leq min(N, 100)1≤K≤min(N,100)
• 1 \leq A_i \leq 10^61≤A​i​​≤10​6​​

Input	Output	Explanation
5 1 1 2 3 4 5	16	The only partition is [1, 5][1,5] with cost (5 - 1)^2 = 16(5−1)​2​​=16
4 2 2 4 3 10	1	The partitions is [1, 3][1,3] and [4, 4][4,4]
11 3 2 4 1 5 3 4 3 5 7 100 100	5	The 33 partitions are [2\ 4\ 1]\ [5\ 3\ 4\ 3\ 5\ 7]\ [100\ 100][2 4 1] [5 3 4 3 5 7] [100 100]

动态凸包

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,a,b) for(int i=a;i<b;i++)
const ll is_query = -(1LL<<);
struct convex_line
{
    ll m,b;
    mutable function<const convex_line*()> succ;
    bool operator<(const convex_line& rhs) const
    {
        if(rhs.b!=is_query) return m < rhs.m;
        const convex_line* s=succ();
        if(s==NULL) return ;
        ll x=rhs.m;
        return 1.0*(b-s->b)<1.0*(s->m-m)*x;
    }
};
struct dcht : public multiset<convex_line>
{
    bool invalid(iterator y)
    {
        auto z=next(y);
        if(y==begin())
        {
            if (z==end()) return ;
            return y->m==z->m && y->b<=z->b;
        }
        auto x=prev(y);
        if(z==end()) return y->m==x->m && y->b<=x->b;
        return 1.0*(x->b-y->b)*(z->m-y->m)>=1.0*(y->b-z->b)*(y->m-x->m);
    } void insert_line(ll m,ll b) //insert any line
    {
        auto y = insert({m,b});
        y->succ = [=] { return next(y) == end() ?  : &*next(y); };
        if (invalid(y))
        {
            erase(y);
            return;
        }
        while (next(y) != end() && invalid(next(y))) erase(next(y));
        while (y != begin() && invalid(prev(y))) erase(prev(y));
    } void remove_line(ll m,ll b)
    {
        auto y=find({m,b});
        if(y==end()) return;
        erase(y);
    } ll eval(ll x)
    {
        auto l=lower_bound({x, is_query});
        return (*l).m * x + (*l).b;
    }
};
const int N=;
const ll inf=(ll)1e18;
ll a[N];
ll dp[][N];
int main()
{
    std::ios::sync_with_stdio(false);
    int n,k;
    cin>>n>>k;
    rep(i,,n+) cin>>a[i];
    rep(i,,) rep(j,,N) dp[i][j]=inf;
    dp[][]=;
    rep(j,,k+)
    {
        dcht cht;
        cht.insert_line(*a[],-dp[j-][]-(a[]*a[]));
        rep(i,,n+)
        {
            dp[j][i]=a[i]*a[i]-cht.eval(a[i]);
            cht.insert_line(*a[i+],-dp[j-][i]-(a[i+]*a[i+]));
        }
    }
    cout<<dp[k][n]<<endl;
    return  ;
}

这份代码也不错