牛客网Java刷题知识点之线程的几种可用状态(新建、可运行、运行、阻塞、死亡)
不多说,直接上干货!
- https://www.nowcoder.com/ta/review-java/review?query=&asc=true&order=&page=13
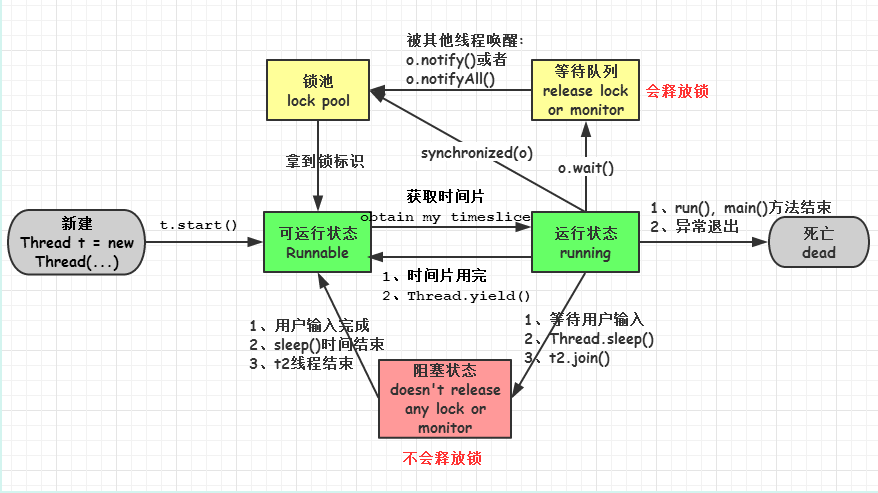
牛客网Java刷题知识点之线程的几种可用状态(新建、可运行、运行、阻塞、死亡)的更多相关文章
- 牛客网Java刷题知识点之Map的两种取值方式keySet和entrySet、HashMap 、Hashtable、TreeMap、LinkedHashMap、ConcurrentHashMap 、WeakHashMap
不多说,直接上干货! 这篇我是从整体出发去写的. 牛客网Java刷题知识点之Java 集合框架的构成.集合框架中的迭代器Iterator.集合框架中的集合接口Collection(List和Set). ...
- 牛客网Java刷题知识点之为什么HashMap和HashSet区别
不多说,直接上干货! HashMap 和 HashSet的区别是Java面试中最常被问到的问题.如果没有涉及到Collection框架以及多线程的面试,可以说是不完整.而Collection框架的 ...
- 牛客网Java刷题知识点之为什么HashMap不支持线程的同步,不是线程安全的?如何实现HashMap的同步?
不多说,直接上干货! 这篇我是从整体出发去写的. 牛客网Java刷题知识点之Java 集合框架的构成.集合框架中的迭代器Iterator.集合框架中的集合接口Collection(List和Set). ...
- 牛客网Java刷题知识点之HashMap的实现原理、HashMap的存储结构、HashMap在JDK1.6、JDK1.7、JDK1.8之间的差异以及带来的性能影响
不多说,直接上干货! 福利 => 每天都推送 欢迎大家,关注微信扫码并加入我的4个微信公众号: 大数据躺过的坑 Java从入门到架构师 人工智能躺过的坑 ...
- 牛客网Java刷题知识点之Java 集合框架的构成、集合框架中的迭代器Iterator、集合框架中的集合接口Collection(List和Set)、集合框架中的Map集合
不多说,直接上干货! 集合框架中包含了大量集合接口.这些接口的实现类和操作它们的算法. 集合容器因为内部的数据结构不同,有多种具体容器. 不断的向上抽取,就形成了集合框架. Map是一次添加一对元素. ...
- 牛客网Java刷题知识点之ArrayList 、LinkedList 、Vector 的底层实现和区别
不多说,直接上干货! 这篇我是从整体出发去写的. 牛客网Java刷题知识点之Java 集合框架的构成.集合框架中的迭代器Iterator.集合框架中的集合接口Collection(List和Set). ...
- 牛客网Java刷题知识点之垃圾回收算法过程、哪些内存需要回收、被标记需要清除对象的自我救赎、对象将根据存活的时间被分为:年轻代、年老代(Old Generation)、永久代、垃圾回收器的分类
不多说,直接上干货! 首先,大家要搞清楚,java里的内存是怎么分配的.详细见 牛客网Java刷题知识点之内存的划分(寄存器.本地方法区.方法区.栈内存和堆内存) 哪些内存需要回收 其实,一般是对堆内 ...
- 牛客网Java刷题知识点之UDP协议是否支持HTTP和HTTPS协议?为什么?TCP协议支持吗?
不多说,直接上干货! 福利 => 每天都推送 欢迎大家,关注微信扫码并加入我的4个微信公众号: 大数据躺过的坑 Java从入门到架构师 人工智能躺过的坑 ...
- 牛客网Java刷题知识点之TCP、UDP、TCP和UDP的区别、socket、TCP编程的客户端一般步骤、TCP编程的服务器端一般步骤、UDP编程的客户端一般步骤、UDP编程的服务器端一般步骤
福利 => 每天都推送 欢迎大家,关注微信扫码并加入我的4个微信公众号: 大数据躺过的坑 Java从入门到架构师 人工智能躺过的坑 Java全栈大联盟 ...
随机推荐
- Java中锁的内存语义
我们都知道,Java中的锁可以让临界区互斥执行.锁是Java并发编程中最重要的同步机制,锁除了可以让临界区互斥执行外,还可以让释放锁的线程向获取同一个锁的线程发送消息.下面是锁的释放-获取的代码: C ...
- php-get和post请求
1.get请求 <?php //判断20130101是否是工作日 //工作日对应结果为 0, 休息日对应结果为 1, 节假日对应的结果为 2: $url='http://www.easybots ...
- hdu 1391 Number Steps(规律)
题意:找规律 思路:找规律 #include<iostream> #include<stdio.h> using namespace std; int main(){ int ...
- RequireJS 配置理解
RequireJS 配置: 1.首先加载RequireJS文件 <script src="//cdn.bootcss.com/require.js/2.1.22/require.js& ...
- 为什么要把页面放在 WEB-INF 路径下?
1.基于不同的功能 JSP 被放置在不同的目录下 这种方法的问题是这些页面文件容易被偷看到源代码,或被直接调用.某些场合下这可能不是个大问题,可是在特定情形中却可能构成安全隐患.用户可以绕过Strut ...
- bzoj 3771 Triple —— FFT
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3771 令多项式的系数是方案数,次数是值: 设 a(x) 为一个物品的多项式,即 a[w[i] ...
- Android开发:显式/隐式Intent
显式跳转 是在已知包名和类名的情况下常用的跳转方法: Intent mIntent = new Intent(); mIntent.setClassName("com.android.set ...
- CSS:CSS 单位
ylbtech-CSS:CSS 单位 1.返回顶部 1. 尺寸 单位 描述 % 百分比 in 英寸 cm 厘米 mm 毫米 em 1em 等于当前的字体尺寸. 2em 等于当前字体尺寸的两倍. 例如, ...
- 双重检查锁实现单例(java)
单例类在Java开发者中非常常用,但是它给初级开发者们造成了很多挑战.他们所面对的其中一个关键挑战是,怎样确保单例类的行为是单例?也就是说,无论任何原因,如何防止单例类有多个实例.在整个应用生命周期中 ...
- Product it again
题意:求解 $$\prod_{1 \leq i \leq n} \prod_{1 \leq j \leq m} {(i,j)}$$ 解法: 满脑子的反演 考虑对于第一个质数 $p$ 的贡献为 $p^{ ...
