《机器学习实战》学习笔记第三章 —— 决策树之ID3、C4.5算法

 (这两个算法似乎都需要y是离散的，而CART算法y是离散或者连续都可以，对应不同的评价标准)

主要内容：

一.决策树模型

二.信息与熵

三.信息增益与ID3算法

四.信息增益比与C4.5算法

五.决策树的剪枝

一.决策树模型

1.所谓决策树，就是根据实例的特征对实例进行划分的树形结构。其中有两种节点：内节点表示一个特征，叶子结点表示一个类（或称为标签）。

2.在决策树中，从根节点开始，对实例的所有特征进行测试，根据测试结果，选择最合适的特征作为依据，将实例分配到其子节点上；此时，每一个子节点都对应着该特征（即父节点上的特征）的一个取值。之后一直递归下去，直到所有节点上所有实例的类都一样、或者特征已经用完。

3.决策树实际上就是一个“if-then”决策模型，其构造过程可用以下伪代码表示：

4.如何寻找划分数据的“最好特征”呢？

根据个人的经验，是选择使得划分前后方差减少得多的那一特征，因为方差越大不确定性越强，信息量就越大。以不确定性最强的那一特征进行划分数据，那么划分之后，不确定性就弱了很多了，即确定性就强了。当然这是个人的直觉，解决这一问题还需要引入信息量中的“熵”和“信息增益”。

5.待解决的疑问：为什么决策树的ID3、C4.5算法使用熵而不是方差来度量信息的不确定性呢？

二.熵

1.在信息论中，如果X为一个随机变量，xi为其中的一个值，那么xi的信息定义为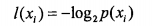：，其中p(xi)是随机变量X出现xi的概率。

可知：熵就是信息的期望值。

2.由定义可知，熵只依赖于X的分布，而与X的取值无关，因此将X的熵记作H(p)：

3.混淆点：在开始的时候，思想一直在“特征（即X）的熵”和“标签（即Y）的熵”之间游荡，而且自己都没发现，所以就越想越混乱，后来搞清了，是：被X划分后，Y的熵。

三.信息增益与ID3算法

1.以下是“条件熵”、“经验熵”、“经验条件熵”的定义：

2.以下是信息增益的定义：

3.信息增益，简单而言，就是划分前后熵的差值。可知在构造决策树的过程中，当选择使得数据划分后信息增益最大的那一特征。

4.ID3算法就是以“信息增益”为基础的决策树构造算法，具体如下：

（其中阈值ε用于预剪枝）

Python代码（没有剪枝）：

 # coding:utf-8
 '''
 Created on Oct 12, 2010
 Decision Tree Source Code for Machine Learning in Action Ch. 3
 @author: Peter Harrington
 '''
 from math import log
 import operator

 def createDataSet():
     dataSet = [[1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']]
     labels = ['no surfacing' ,'flippers']
     # change to discrete values
     return dataSet, labels

 '''dataSet为二维列表'''
 def calcShannonEnt(dataSet):  # 计算熵
     numEntries = len(dataSet)
     labelCounts = {}  # 统计每个标签出现的次数
     for featVec in dataSet:  # the the number of unique elements and their occurance
         currentLabel = featVec[-1]  # 获得标签
         if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
         labelCounts[currentLabel] += 1  #累加
     shannonEnt = 0.0
     for key in labelCounts: #枚举每个标签，计算熵
         prob = float(labelCounts[key] ) /numEntries     #概率
         shannonEnt -= prob * log(prob ,2)  # 熵
     return shannonEnt

 '''axis为划分数据集的特征，axis为索引；value为需要返回的特征的值。'''
 def splitDataSet(dataSet, axis, value):
     retDataSet = []
     for featVec in dataSet:
         if featVec[axis] == value:  #如果为要返回的那一类，则记录下来。不用在记录axis特征上的值
             reducedFeatVec = featVec[:axis]  # chop out axis used for splitting
             reducedFeatVec.extend(featVec[axis+1:])
             retDataSet.append(reducedFeatVec)
     return retDataSet

 def chooseBestFeatureToSplit(dataSet):  #选择划分数据集获得的信息增益最大的特征，返回其下标
     numFeatures = len(dataSet[0]) - 1  # 获取特征树
     baseEntropy = calcShannonEnt(dataSet)       #划分前的熵
     bestInfoGain = 0.0; bestFeature = -1        #两个变量用于当前的最大信息增益以及此时的特征
     for i in range(numFeatures):  # 枚举每一个特征（的下标）
         featList = [example[i] for example in dataSet  ]  # 获取该特征的所有值
         uniqueVals = set(featList)  # 去重
         newEntropy = 0.0    #新的熵
         for value in uniqueVals:    #计算新的熵
             subDataSet = splitDataSet(dataSet, i, value)
             prob = len(subDataSet ) /float(len(dataSet))
             newEntropy += prob * calcShannonEnt(subDataSet)
         infoGain = baseEntropy - newEntropy  # 计算信息增益
         if (infoGain > bestInfoGain):  # 更新
             bestInfoGain = infoGain
             bestFeature = i
     return  bestFeature   # returns an integer

 def majorityCnt(classList):     #获取当前数据集的最多数类别，用于当所有特征都划分玩之后仍不能区分所有类别
     classCount ={}
     for vote in classList:
         if vote not in classCount.keys(): classCount[vote] = 0
         classCount[vote] += 1
     sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
     return sortedClassCount[0][0]

 '''dataSet为二维列表,labels为一维列表。返回的是一个嵌套字典以表示树形结构'''
 def createTree(dataSet ,labels):        #递归构造划分树
     classList = [example[-1] for example in dataSet]    #获取所有标签
     if classList.count(classList[0]) == len(classList):     #当列表中所有元素的标签都一样，直接返回
         return classList[0]
     if len(dataSet[0]) == 1: #当所有标签都划分完，用数量最多的标签去代表这个列表的标签
         return majorityCnt(classList)
     bestFeatIndex = chooseBestFeatureToSplit(dataSet)    #获取最佳的划分特征的下标
     bestFeat = labels[bestFeatIndex]            #获取最佳的划分特征（主要是为了构造树形字典）
     myTree = {bestFeat :{}}        #构造当前的树
     del(labels[bestFeatIndex])       #删除最佳特征
     featValues = [example[bestFeatIndex] for example in dataSet]     #获取最佳特征的所有值
     uniqueVals = set(featValues)        #去重
     for value in uniqueVals:
         subLabels = labels[:]  # 复制多一份特征列表，因为在构造的时候会改变其值。
         myTree[bestFeat][value] = createTree(splitDataSet(dataSet, bestFeatIndex, value) ,subLabels)    #获取每一个分支
     return myTree

 def classify(inputTree ,featLabels ,testVec):   #利用划分树进行分类
     firstStr = inputTree.keys()[0]  #获取划分当前节点的特征
     secondDict = inputTree[firstStr]    #获取子树，为一个嵌套字典
     featIndex = featLabels.index(firstStr)  #获取划分特征的在特征列表的下标
     value = testVec[featIndex]            #获取输入数据在该特征下的值
     branchTree = secondDict[value]      #获取与该值相对应的分支
     if isinstance(branchTree, dict):    #非叶子结点，则继续递归
         classLabel = classify(branchTree, featLabels, testVec)
     else: classLabel = branchTree       #到达叶子结点，则标签已经确定，直接返回
     return classLabel

 def storeTree(inputTree ,filename):     #将决策树保存到磁盘中
     import pickle
     fw = open(filename ,'w')
     pickle.dump(inputTree ,fw)
     fw.close()

 def grabTree(filename):     #从磁盘中读取决策树
     import pickle
     fr = open(filename)
     return pickle.load(fr)

 dataSet, labels = createDataSet()
 myTree = createTree(dataSet,labels)
 print myTree
 """
     输出如下：
     {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
 """

四.信息增益比与C4.5算法

1.“信息增益”比好好的，为什么又要多出一个“信息增益比”呢？

因为：以信息增益作为选择特征进行数据划分的依据，存在偏向于选择取值比较多的特征的问题，而“信息增益比”可以校正这一问题。

2.怎么解释这个式子呢？

（截图来自：决策树--信息增益，信息增益比，Geni指数的理解 ）

3.C4.5算法就是以“信息增益比”为基础的决策树构造算法。其算法步骤直接将“信息增益”改为“信息增益比”即可。

五.决策树的剪枝

1.直接依据训练数据一直往下构造决策树，虽然能很好地适应训练数据本身，但却容易出现“过拟合”。为此需要做适当的剪枝，其中有“预剪枝”和“后剪枝”。

2.预剪枝：如上述的ID3算法通过设置合适的阈值ε来限制“生枝”，即假如某个结点的最大信息增益小于阈值，就停止继续划分，而使其成为叶子结点。然而听说这个阈值ε似乎不太好调。

3.后剪枝，即在决策树生成之后，再作适当的剪枝。有关后剪枝的数学解释：

对于5.11式：类似于带正则项的损失函数，可知第二项就是正则项，第一项就是不带正则项的损失函数，但是要怎么理解它呢？

《决策树损失函数对Nt的理解》可很好地解释其所代表的含义。

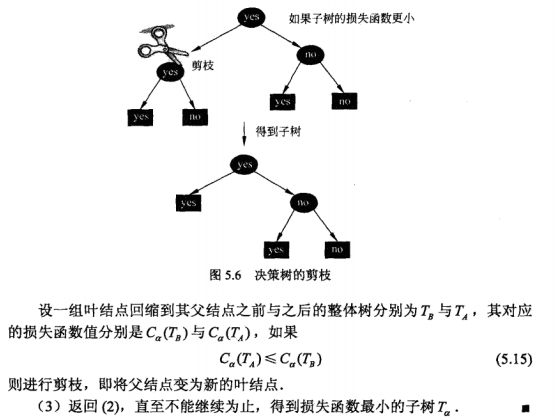
4.决策树剪枝部分的算法如下：