Dance links算法

　　其实Dance links只是一种数据结构，Dance links 才是一种算法。dacing links x就是一个高效的求解该类问题的算法，而这种算法，基于交叉十字循环双向

链表。下面是双向十字链表的示意图：

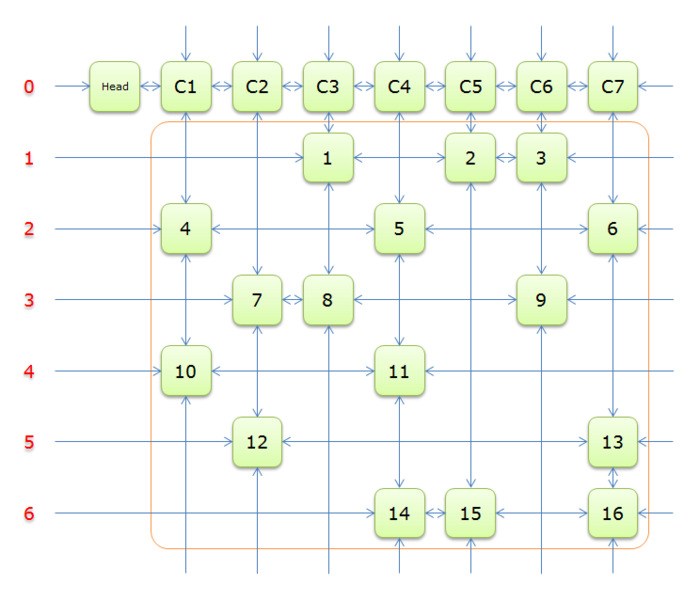
下面给一个使用这个算法模板的裸题：

Exact Cover

Description:

There is an N*M matrix with only 0s and 1s, (1 <= N,M <= 1000). An exact cover is a selection of rows such that every column has a 1 in exactly one of the selected rows. Try to find out the selected rows.

Sample Input:

6 7

3 1 4 7

2 1 4

3 4 5 7

3 3 5 6

4 2 3 6 7

2 2 7

Sample Output:

3 2 4 6

参考代码：

 #include<stdio.h>
 #include<iostream>
 using namespace std;
 const int maxnode =  *  + ;
 const int maxN =  + ;
 const int maxM =  + ;

 struct DLX {
     int n,m, size;                    //n行数，m列数，szie节点数
     int U[maxnode], D[maxnode], L[maxnode], R[maxnode], Col[maxnode], Row[maxnode];
     int H[maxN], S[maxM];            //H[i]第i行的第一个节点，S[j]第j列中节点的个数
     int ansd, ans[maxN];            //ansd解包含的行数，ans[]解

     void init(int _n, int _m)        //初始化十字链表
     {
         n = _n;
         m = _m;
         for (int i = ; i <= m; i++)
         {
             Col[i] = i; Row[i] = ;
             U[i] = D[i] = i;
             L[i] = i + ; R[i] = i - ;
             S[i] = ;
         }
         R[] = m; L[m] = ;
         size = m;
         for (int i = ; i <= n; i++)
             H[i] = -;
     }
     void link(int r, int c)        //在第r行、c列插入一个节点
     {　　　　　　　　　　　　　　　　　　//注意，这里向下为方向
         size++;
         Col[size] = c;
         Row[size] = r;
         S[c]++;
         D[size] = D[c];
         U[D[c]] = size;
         U[size] = c;
         D[c] = size;
         if (H[r] == -)
             H[r] = R[size] = L[size] = size;
         else
         {
             R[size] = R[H[r]];
             L[R[H[r]]] = size;
             L[size] = H[r];
             R[H[r]] = size;
         }
     }
     void remove(int c)            //移除第c列及列上节点所在的行
     {
         L[R[c]] = L[c];
         R[L[c]] = R[c];
         for (int i = D[c]; i != c; i = D[i])
             for (int j = L[i]; j != i ; j = L[j])
             {
                 D[U[j]] = D[j];
                 U[D[j]] = U[j];
                 --S[Col[j]];
             }
     }
     void resume(int c)        //恢复第c列及列上节点所在的行，与remove刚好相反
     {
         for(int i = U[c];i != c;i = U[i])
             for (int j = R[i]; j != i; j = R[j])
             {
                 ++S[Col[j]];
                 D[U[j]] = j;
                 U[D[j]] = j;
             }
         L[R[c]] = c;
         R[L[c]] = c;
     }
     bool Dance(int d)        //d为搜索的深度
     {
         if (R[] == )
         {
             ansd = d;
             return true;
         }
         int c = R[];
         for (int i = R[]; i != ; i = R[i])
             if (S[i] < S[c])
                 c = i;
         remove(c);
         for (int i = D[c]; i != c; i = D[i])    //逐个尝试
         {
             ans[d] = Row[i];
             for (int j = R[i]; j != i; j = R[j])
                 remove(Col[j]);
             if (Dance(d + ))    return true;
             for (int j = L[i]; j != i; j = L[j])
                 resume(Col[j]);
         }
         resume(c);            //这个可有可无，写只是为了完整性
         return false;
     }
 };

 DLX g;
 int main()
 {
     int n, m;

     while (scanf("%d%d",&n,&m) == )
     {
         g.init(n, m);
         for (int i = ; i <= n; i++)
         {
             int num, j;
             scanf("%d", &num);
             while (num--)
             {
                 scanf("%d", &j);
                 g.link(i, j);
             }
         }
         if (!g.Dance())
             printf("NO\n");
         else
         {
             printf("%d", g.ansd);
             for (int i = ; i < g.ansd; i++)
                 printf(" %d", g.ans[i]);
             printf("\n");
         }
     }
     return ;
 }

有什么不对的地方，多谢指教。