神经网络的BP推导过程

神经网络的BP推导过程

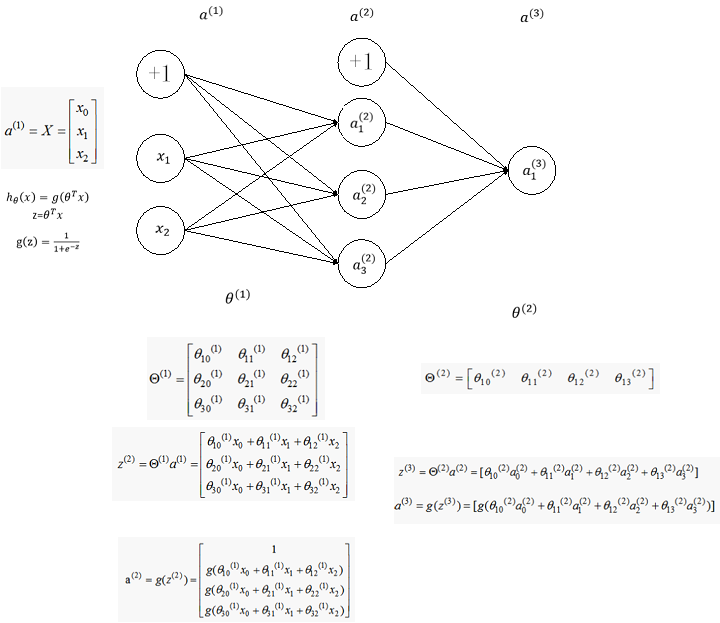
下面我们从一个简单的例子入手考虑如何从数学上计算代价函数的梯度，考虑如下简单的神经网络，该神经网络有三层神经元，对应的两个权重矩阵,为了计算梯度我们只需要计算两个偏导数即可：

首先计算第二个权重矩阵的偏导数，即

首先需要在之间建立联系，很容易可以看到的值取决于,而,而又是由取sigmoid得到，最后,所以他们之间的联系可以如下表示：

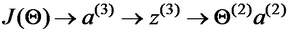
按照求导的链式法则，我们可以先求对的导数，然后乘以对的导数，即

由于

不难计算

令

上式可以重写为

接下来仅需要计算即可，由于

忽略前面的

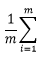
以及正则项

设k=1得到

这里只对一个example推导，最后累加即可

因此

得到下面的求导过程

由于

，计算如下，得

至此我们得到了

接下去我们需要求的偏导数，的依赖关系如下：

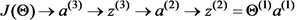
根据链式求导法则有

分别计算等式右边的三项可得

带入后得

令

上式可以重写为

将上面的结果放在一起，我们得到对两个权重矩阵的偏导数为：

观察上面的四个等式，我们发现

• 偏导数可以由当层神经元向量与下一层的误差向量相乘得到
• 当前层的误差向量可以由下一层的误差向量与权重矩阵的乘积得到

所以可以从后往前逐层计算误差向量，然后通过简单的乘法运算得到代价函数对每一层权重矩阵的偏导数。

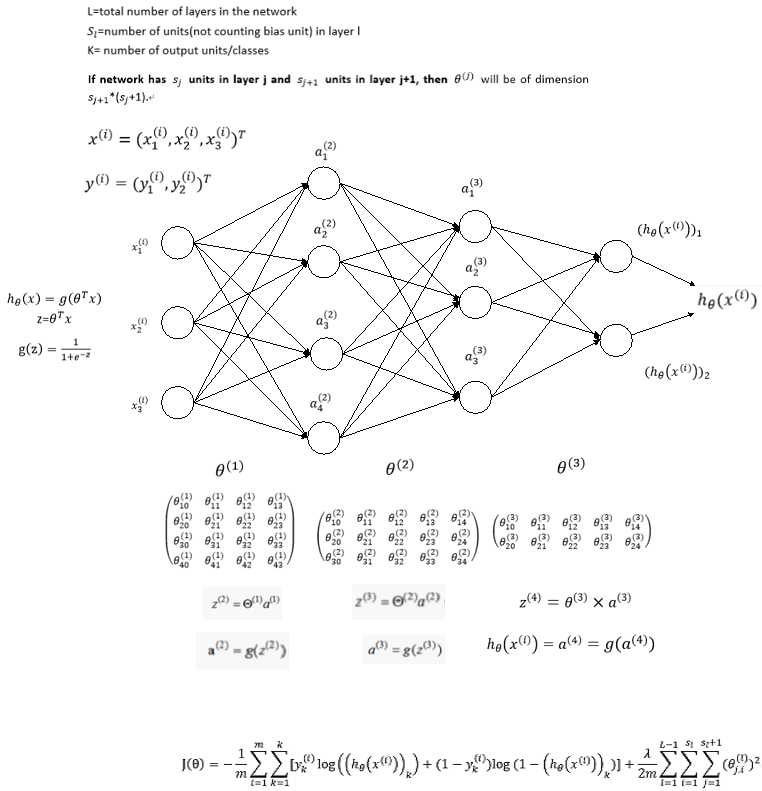
假设我们有m个训练example,L层神经网络，并且此处考虑正则项，即

初始化：设置(理解为对第l层的权重矩阵的偏导累加值，每一个训练的偏导数累加值，最后再除以样本数得到均值)

For k=1:m

设置 =

通过前向传播算法(FP)计算对各层的预测值,其中l=1,2,3,4…,L

计算最后一层的误差向量,利用后向传播算法(BP)从后至前逐层计算误差向量,计算公式为

更新

End//

计算梯度：

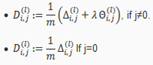
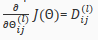
附录：