八皇后问题（DFS）

题目描述:

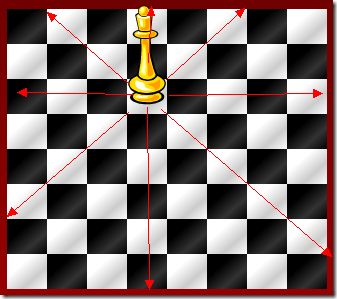
要在国际象棋棋盘中放八个皇后，使任意两个皇后都不能互相吃，皇后能吃同一行、同一列，同一对角线上（两个方向的对角线）的任意棋子。现在给一个整数n(n<=92)，输出前n种的摆法。

输入格式:

输入一个整数n。

输出格式:

输出共n行。

每行8个数，表示每行所放的列号，每个数输出占4列。

样例输入:

3

样例输出:

1   5   8   6   3   7   2   4
1   6   8   3   7   4   2   5
1   7   4   6   8   2   5   3

思路：DFS，把每一个格子试一次。

提示：

确定两个棋子在不在统同一行，同一列，同一对角线的方法：

如下图，如果两个棋子在同一行，则i1=i2；

如果两个棋子在同一行列，则j1=j2；

如果两个棋子在同对角线，则i1+j1=i2+j2；

不多说了，上代码：

#include<bits/stdc++.h>
using namespace std;
int a[],b[],c[],d[],n,sum,m;//a[9],b[9],直线, c[17],d[17],对角线
void print(){
    for(int i=;i<=n;i++)printf("%4d",d[i]);
    cout<<endl;
}
void search(int row){//DFS
    if(row>n){//如果放满了就打印(print函数)
        sum++;
        if(sum<=m)print();
        return;//返回
    }
    for(int i=;i<=n;i++){
        if(a[i]== && b[row+i]== && c[row-i+]==){
            a[i]=;
            b[row+i]=;
            c[row-i+]=;//放棋子
            d[row]=i;//记录
            search(row+);//递归
            a[i]=;
            b[row+i]=;
            c[row-i+]=;//恢复
        }
    }
}
int main(){
    n=;//八皇后,故n=8
    cin>>m;
    search();
    return ;
}