LOJ 3043: 洛谷 P5280: 「ZJOI2019」线段树

题目传送门：LOJ #3043。

题意简述：

你需要模拟线段树的懒标记过程。

初始时有一棵什么标记都没有的 \(n\) 阶线段树。

每次修改会把当前所有的线段树复制一份，然后对于这些线段树实行一次区间修改操作。

即每次修改后线段树棵数翻倍，第 \(i\) 次修改后，线段树共有 \(2^i\) 棵。

区间修改操作的伪代码如下：

和我日常写的递归式线段树完全一致。

每次询问你这些线段树中有懒标记的节点总数。

修改和询问的总个数为 \(q\)，\(1\le n,q\le 10^5\)。

题解：

灵感来源自 Sooke 的题解。

考察一次区间修改操作会影响到的节点，共有 \(5\) 类：

1. 与修改区间相交，但不包含在修改区间内部的节点（浅紫色）。

2. 包含在修改区间内部，但其父亲不存在或不包含在修改区间内部（浅蓝色）。

3. 与修改区间相离，但其父亲与修改区间相交（浅橙色）。

4. 包含在修改区间内部，且其父亲也包含在修改区间内部（深蓝色）。

5. 与修改区间相离，且其父亲也与修改区间相离（深橙色）。

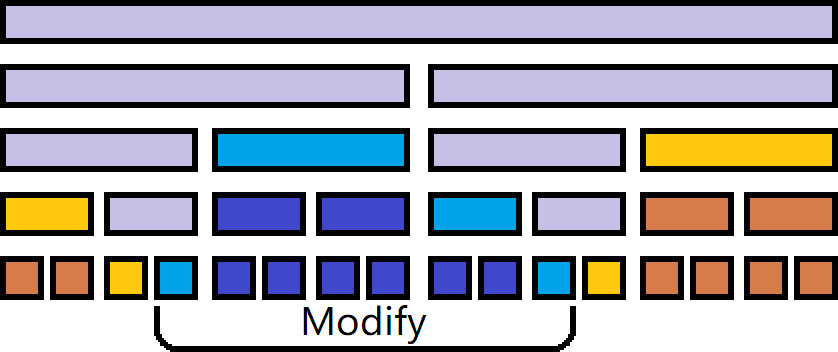
将节点分为这 \(5\) 类并不是没有根据的，可以发现：

若伪代码运行到了第 \(17\) 行，则访问到的是第 \(1\) 类节点。

若伪代码运行到了第 \(14\) 行，则访问到的是第 \(2\) 类节点。

若伪代码运行到了第 \(11\) 行，则访问到的是第 \(3\) 类节点。

而第 \(4,5\) 类节点分别是第 \(2,3\) 类节点的子孙。

根据线段树的复杂度，第 \(1,2,3\) 类节点的个数均为 \(\mathcal{O}(\log n)\)，而第 \(4,5\) 类节点的个数为 \(\mathcal{O}(n)\)。

接下来分析每次操作时受到影响的节点：

对于第 \(1\) 类节点，操作后它们必然无懒标记。

对于第 \(2\) 类节点，操作后它们必然有懒标记。

对于第 \(3\) 类节点，操作后它们有无懒标记取决于操作前这个节点到根的链上有无懒标记。

对于第 \(4,5\) 类节点，操作后它们不受影响。

我们考虑维护每次操作后每个节点 \(u\) 有懒标记的树的占比，即在 \(2^i\) 棵树中，节点 \(u\) 有懒标记的树的比值，记作 \(\mathrm{f}[u]\)。

同时，因为第 \(3\) 类节点需要额外信息，维护每次操作后每个节点 \(u\) 到根的路径上有懒标记的树的占比，记作 \(\mathrm{g}[u]\)。

接下来我们考虑一次操作后，每个节点的信息如何更新，注意到同类节点的更新方式是相同的：

对于第 \(1\) 类节点，一半保持原样，另一半无标记，所以 \(\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle=\left\langle\frac{1}{2}\mathrm{f}[u],\frac{1}{2}\mathrm{g}[u]\right\rangle\)。

对于第 \(2\) 类节点，一半保持原样，另一半有标记，所以 \(\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle=\left\langle\frac{1}{2}\mathrm{f}[u]+\frac{1}{2},\frac{1}{2}\mathrm{g}[u]+\frac{1}{2}\right\rangle\)。

对于第 \(3\) 类节点，一半保持原样，另一半的标记取决于 \(u\) 到根的路径，所以 \(\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle=\left\langle\frac{1}{2}(\mathrm{f}[u]+\mathrm{g}[u]),\mathrm{g}[u]\right\rangle\)。

对于第 \(4\) 类节点，一半保持原样，另一半标记不受影响，但到根的路径上一定有标记，所以 \(\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle=\left\langle\mathrm{f}[u],\frac{1}{2}\mathrm{g}[u]+\frac{1}{2}\right\rangle\)。

对于第 \(5\) 类节点，一半保持原样，另一半标记不受影响，到根的路径上的标记也不受影响，所以 \(\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle=\left\langle\mathrm{f}[u],\mathrm{g}[u]\right\rangle\)。

第 \(5\) 类节点的信息没有更改，第 \(4\) 类节点仅有 \(\mathrm{g}\) 有更改，因为第 \(4\) 类节点有 \(\mathcal{O}(n)\) 个，所以必须采用打懒标记的方法来维护。

而对于前 \(3\) 类，直接维护即可。

再多维护一个 \(\mathrm{Sf}[u]\) 表示 \(u\) 的子树中 \(\mathrm{f}[v]\) 值之和即可统计答案。

#include <cstdio>

typedef long long LL;
const int Mod = 998244353;
const int Inv2 = 499122177;
const int MS = 1 << 18;

inline int Add(int x, int y) {
	return (x += y) >= Mod ? x - Mod : x;
}

int N, M;

int f[MS], g[MS], Sf[MS], T[MS];
inline void P(int i, int x) {
	g[i] = ((LL)g[i] * x + 1 - x + Mod) % Mod;
	T[i] = (LL)T[i] * x % Mod;
}
inline void Upd(int i, int Ty) {
	if (Ty) Sf[i] = f[i];
	else Sf[i] = Add(f[i], Add(Sf[i << 1], Sf[i << 1 | 1]));
}
inline void Psd(int i) {
	P(i << 1, T[i]);
	P(i << 1 | 1, T[i]);
	T[i] = 1;
}
void Build(int i, int l, int r) {
	T[i] = 1;
	if (l != r) {
		Build(i << 1, l, (l + r) >> 1);
		Build(i << 1 | 1, ((l + r) >> 1) + 1, r);
	}
}
void Mdf(int i, int l, int r, int a, int b) {
	if (r < a || b < l) {
		f[i] = (LL)(f[i] + g[i]) * Inv2 % Mod;
		Upd(i, l == r);
		return ;
	}
	if (a <= l && r <= b) {
		f[i] = (LL)(f[i] + 1) * Inv2 % Mod;
		Upd(i, l == r);
		P(i, Inv2);
		return ;
	}
	Psd(i);
	f[i] = (LL)f[i] * Inv2 % Mod;
	g[i] = (LL)g[i] * Inv2 % Mod;
	Mdf(i << 1, l, (l + r) >> 1, a, b);
	Mdf(i << 1 | 1, ((l + r) >> 1) + 1, r, a, b);
	Upd(i, 0);
}

int main() {
	scanf("%d%d", &N, &M);
	Build(1, 1, N);
	for (int m = 1, C = 1; m <= M; ++m) {
		int op, l, r;
		scanf("%d", &op);
		if (op == 1) {
			scanf("%d%d", &l, &r);
			Mdf(1, 1, N, l, r);
			C = Add(C, C);
		}
		else printf("%lld\n", (LL)C * Sf[1] % Mod);
	}
	return 0;
}