hihoCoder #1106 : Koch Snowflake 微软苏州校招笔试（1月17日）

描述

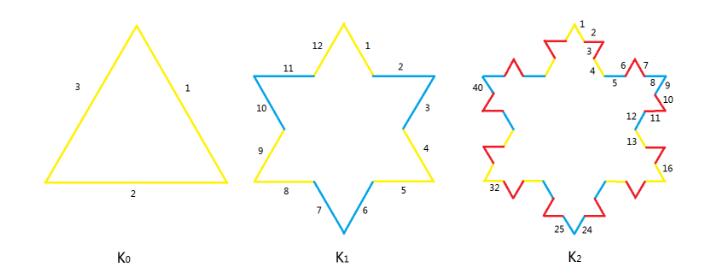
Koch Snowflake is one of the most famous factal. It is built by starting with an equilateral triangle, removing the inner third of each side, building another equilateral triangle at the location where the side was removed, and then repeating the process indefinitely.

Let Kn be the Koch Snowflake after n-th iteration. It is obvious that the number of sides of Kn, Nn, is 3*4n. Let's number the sides clockwisely from the top of Koch Snowflake.

Let si,n be the i-th side of Kn. The generation of si,n is defined as the smallest m satifying si,n is a part of the sides of Km. For example, in the above picture, the yellow sides are of generation 0; the blue sides are of generation 1; the red sides are of generation 2.

Given a side si,n, your task is to calculate its generation.

输入

The input contains several test cases.

The first line contains T(T <= 1000), the number of the test cases.

The following T lines each contain two numbers, i(1 <= i <= 10^9) and n(0 <= n <= 1000). Your task is to calculate the generation of side si,n.

输出

For each test case output the generation of the side.

样例输入

5
1 0
1 1
2 1
10 2
16 3

样例输出

0
0
1
2
0

题目大意

给定一个三角形，每经过一次迭代，每一条边变成4条小一点的边。告诉你迭代的次数，以及边的编号，求该条边是第几次迭代出现的边。

解题思路

本题是一道数学题，用找规律的方法即可解决。

我们先来观察一下一条边在两次迭代之前的变化情况：

其中黄线为我们选中的一条边，我们并不知道它是第几次迭代产生的边。蓝线是第n次迭代后产生的新边，因此其代数为n。

假设迭代前的边为原图形中第i条边，那么迭代后对应的新图形中第4(i-1)+1 .. 4(i-1)+4这四条边。

在新的四条边中，我们可以知道4(i-1)+2和_4(i-1)+3_这两条边一定是当前迭代产生新边。同时我们可以根据其序号，算出原来的i。

由此我们可以得到结论，对于第n次迭代后的第k条边，若：

• k mod 4 == 2或3：则该边一定是第n次迭代产生的新边；
• k mod 4 == 0或1：则该边不是第n次迭代产生的新边，且该边在第n-1次迭代中对应的是第ceil(k/4)条边。(ceil为上取整函数)

利用这个性质，对于给定的k和n，我们先判定第k条边是否是第n次迭代产生的新边。若是，则直接返回n；否则我们根据第二条性质，计算出的新的k' = ceil(k/4),n' = n - 1，再次代入进行计算。

我们可以写出这个递归的程序：

calc(k, n):
    If (n == 0) Then
        Return 0;   // 若n = 0时，该边一定属于初始图形
    End If
    If (k mod 4 == 2 or k mod 4 == 3) Then
        Return n;
    End If
    Return calc(ceil(k/4), n - 1);

得到了该函数，本题也就迎刃而解了。

 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cstdio>
 #include <vector>
 #include <cstdlib>
 #include <iomanip>
 #include <cmath>
 #include <ctime>
 #include <map>
 #include <set>
 using namespace std;
 #define lowbit(x) (x&(-x))
 #define max(x,y) (x>y?x:y)
 #define min(x,y) (x<y?x:y)
 #define MAX 100000000000000000
 #define MOD 1000000007
 #define pi acos(-1.0)
 #define ei exp(1)
 #define PI 3.141592653589793238462
 #define INF 0x3f3f3f3f3f
 #define mem(a) (memset(a,0,sizeof(a)))
 typedef long long ll;
 ll gcd(ll a,ll b){
     return b?gcd(b,a%b):a;
 }
 const int N=;
 const int mod=1e9+;
 int t,i,n;
 int main()
 {
     scanf("%d",&t);
     while(t--){
         scanf("%d %d",&i,&n);
         while(n!=){
             if(i%==||i%==) break;
             i=i/+i%;
             n--;
         }
         printf("%d\n",n);
     }
     return ;
 }