对ThreadLocal实现原理的一点思考

前言

在《透彻理解Spring事务设计思想之手写实现》中，已经向大家揭示了Spring就是利用ThreadLocal来实现一个线程中的Connection是同一个，从而保证了事务。本篇博客将带大家来深入分析ThreadLocal的实现原理。

ThreadLocal是什么、有什么、能做什么？

ThreadLocal提供一个线程（Thread）局部变量，访问到某个变量的每一个线程都拥有自己的局部变量。说白了，ThreadLocal就是想在多线程环境下去保证成员变量的安全。

ThreadLocal提供的方法

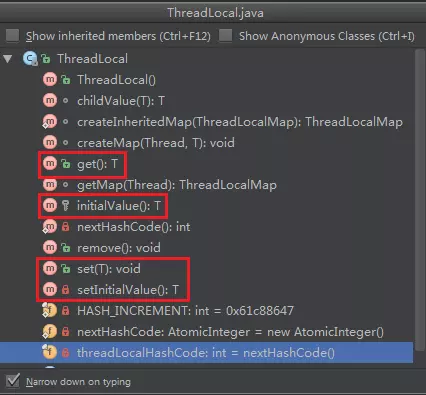
对于ThreadLocal而言，常用的方法，就是get/set/initialValue方法。

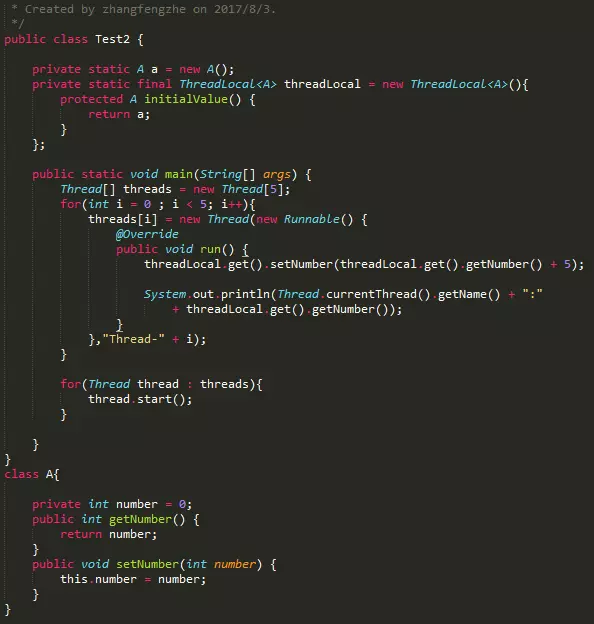
我们先来看一个例子

运行结果

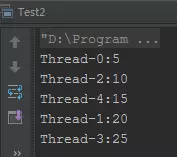
很显然，在这里，并没有通过ThreadLocal达到线程隔离的机制，可是ThreadLocal不是保证线程安全的么？这是什么鬼？
虽然，ThreadLocal让访问某个变量的线程都拥有自己的局部变量，但是如果这个局部变量都指向同一个对象呢？这个时候ThreadLocal就失效了。仔细观察下图中的代码，你会发现，threadLocal在初始化时返回的都是同一个对象a！

看一看ThreadLocal源码

我们直接看最常用的set操作：

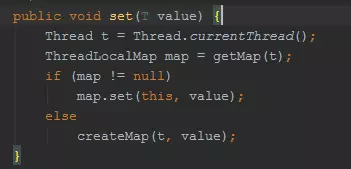
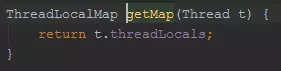
你会看到，set需要首先获得当前线程对象Thread；
然后取出当前线程对象的成员变量ThreadLocalMap；
如果ThreadLocalMap存在，那么进行KEY/VALUE设置，KEY就是ThreadLocal；
如果ThreadLocalMap没有，那么创建一个；
说白了，当前线程中存在一个Map变量，KEY是ThreadLocal，VALUE是你设置的值。

看一下get操作：

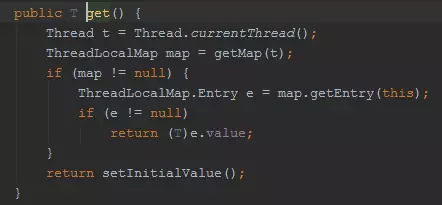
这里其实揭示了ThreadLocalMap里面的数据存储结构，从上面的代码来看，ThreadLocalMap中存放的就是Entry，Entry的KEY就是ThreadLocal，VALUE就是值。

ThreadLocalMap.Entry：

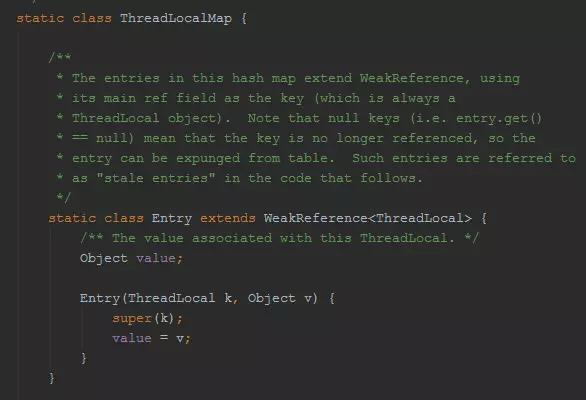
在JAVA里面，存在强引用、弱引用、软引用、虚引用。这里主要谈一下强引用和弱引用。

强引用，就不必说了，类似于：
A a = new A();
B b = new B();
考虑这样的情况：

C c = new C(b);
b = null;

考虑下GC的情况。要知道b被置为null，那么是否意味着一段时间后GC工作可以回收b所分配的内存空间呢？答案是否定的，因为即便b被置为null，但是c仍然持有对b的引用，而且还是强引用，所以GC不会回收b原先所分配的空间！既不能回收利用，又不能使用，这就造成了内存泄露。

那么如何处理呢？

可以c = null;也可以使用弱引用！（WeakReference w = new WeakReference(b);）

分析到这里，我们可以得到：

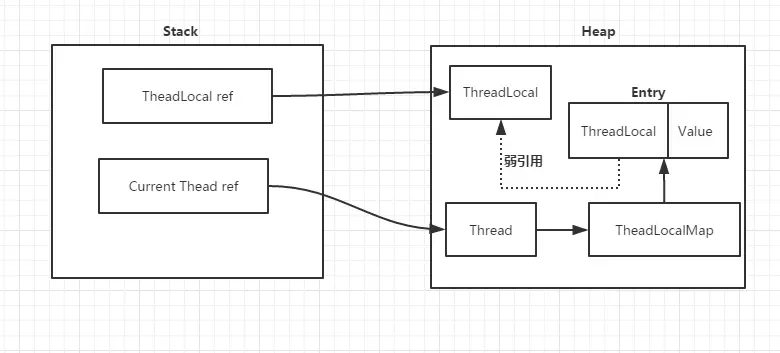
这里我们思考一个问题：ThreadLocal使用到了弱引用，是否意味着不会存在内存泄露呢？

首先来说，如果把ThreadLocal置为null，那么意味着Heap中的ThreadLocal实例不在有强引用指向，只有弱引用存在，因此GC是可以回收这部分空间的，也就是key是可以回收的。但是value却存在一条从Current Thread过来的强引用链。因此只有当Current Thread销毁时，value才能得到释放。

因此，只要这个线程对象被gc回收，就不会出现内存泄露，但在threadLocal设为null和线程结束这段时间内不会被回收的，就发生了我们认为的内存泄露。最要命的是线程对象不被回收的情况，比如使用线程池的时候，线程结束是不会销毁的，再次使用的，就可能出现内存泄露。

那么如何有效的避免呢？

事实上，在ThreadLocalMap中的set/getEntry方法中，会对key为null（也即是ThreadLocal为null）进行判断，如果为null的话，那么是会对value置为null的。我们也可以通过调用ThreadLocal的remove方法进行释放！

好了，到这里，ThreadLocal的剖析就完成了，自己对ThreadLocal的认识又深入了些，^_^

作者：张丰哲
链接：https://www.jianshu.com/p/ee8c9dccc953
来源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。