算法进阶面试题01——KMP算法详解、输出含两次原子串的最短串、判断T1是否包含T2子树、Manacher算法详解、使字符串成为最短回文串
1、KMP算法详解与应用
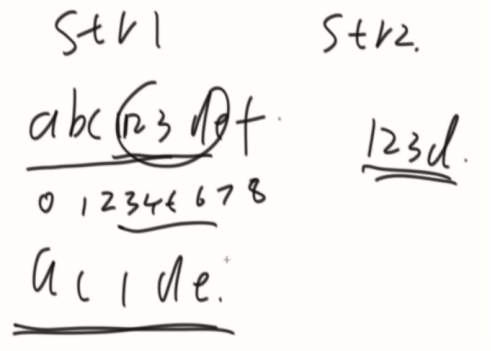
子序列:可以连续可以不连续。
子数组/串:要连续
暴力方法:逐个位置比对。
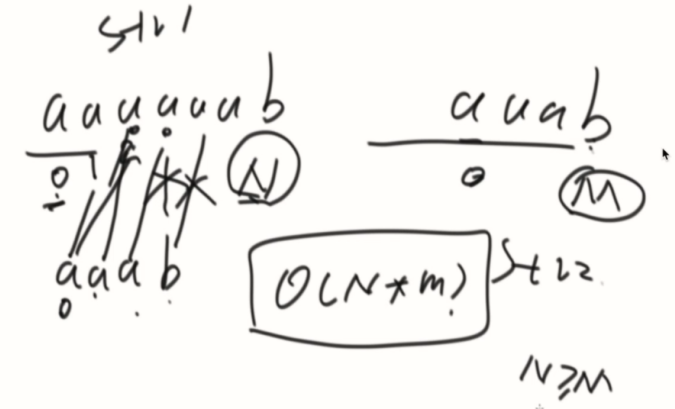
KMP:让前面的,指导后面。
概念建设:
d的最长前缀与最长后缀的匹配长度为3。(前缀不能到最后一个,后缀也不能到第一个)

先计算出str2的全部匹配信息。

一路相等,直到X与Y不匹配,根据X位置的最长前后缀信息加速。
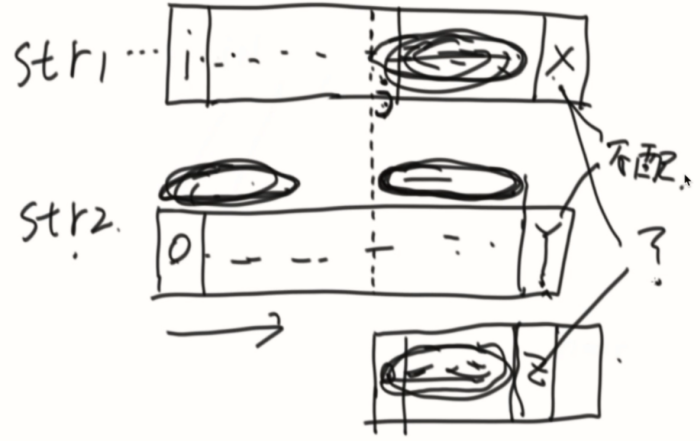
例子:
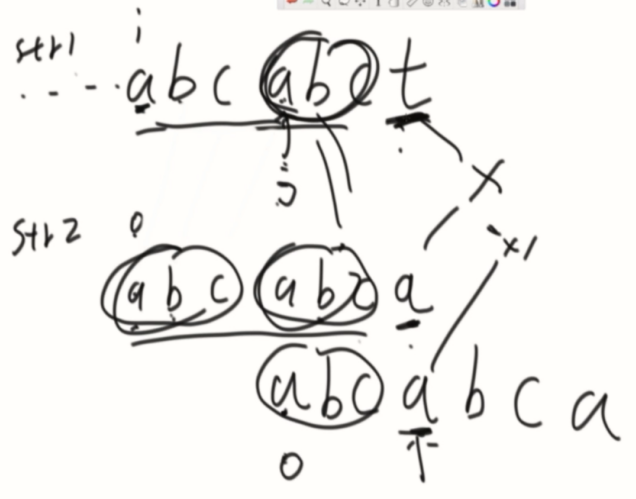
用str1的第一个不同的位置(t)从str2最长前缀的下标位置(a)开始比对。
(加强)再说说流程,举例子:
j是推到和后缀等量的位置,如果碰到一个字符最长前后缀为0(该位置没得加速),那么匹配字符就只挪动一位,再继续逐一比对。
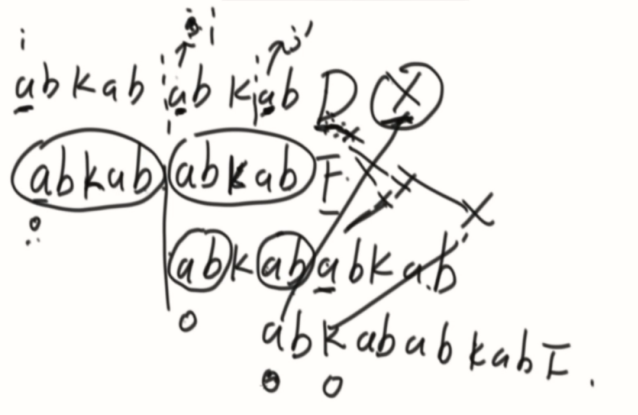
代码里面的实现:匹配到了甲乙位置,甲不动,乙根据Y最长前后缀的值去到前面。和甲继续比对。由于有等量的东西,所以就跳过了一部分值的比对。
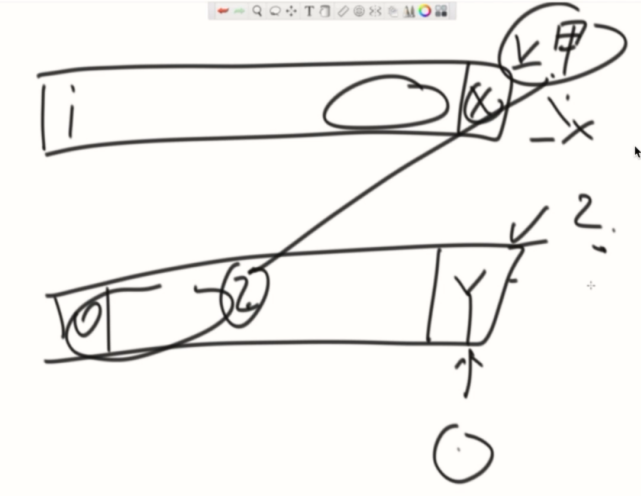
实质:
为什么i~j这些位置可以判断出,配不出str2?
假设可以从k出发配出全部str2,那么k~x应该和str2的前段等量相等(Y的前缀),k~x也对应着str2中的另一部分(Y的后缀),导致和之前找出的最长前后缀不一致,所以在之前的最长前后缀正确的情况下,是不可能的。
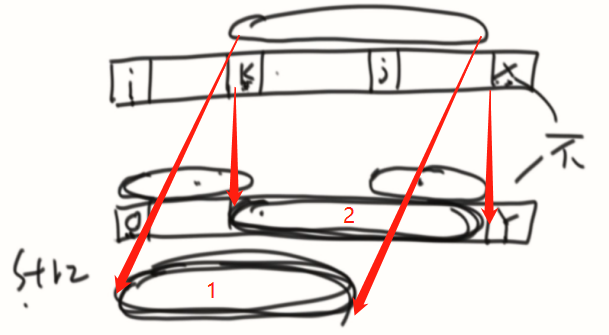
next数组怎么求?
数学归纳法,例如:a的位置,根据判断a的前一个b,和b的最长前缀后的一个是否相等来决定。
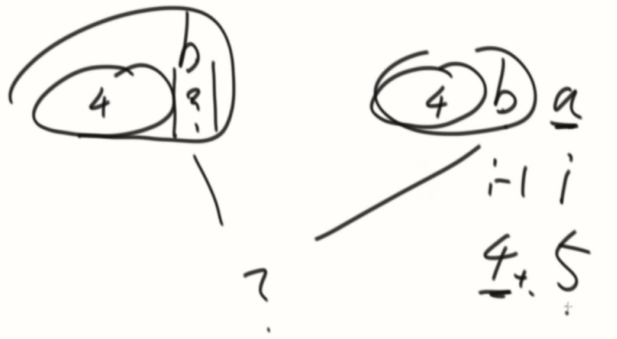
如果不等,就拿b最长前缀的下一个c的最长前缀的下一个来比对,一样就c的+1,不一样就继续拆分来看,一直到拆分不了才设置为0。
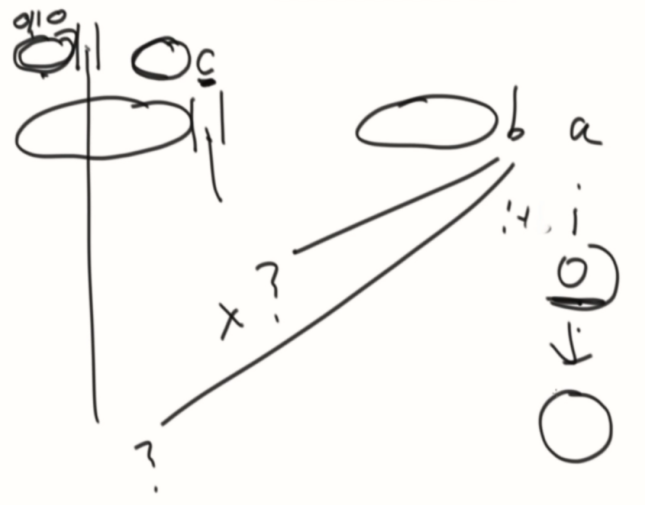
例子:
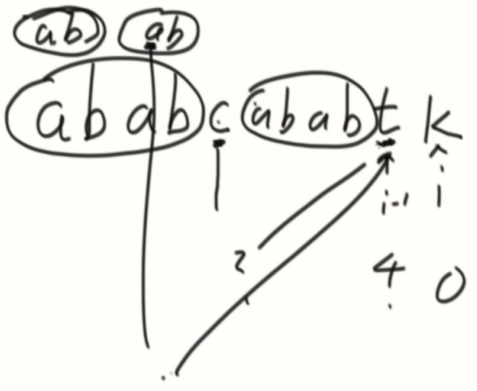
变换一下,把t变为a的情况:
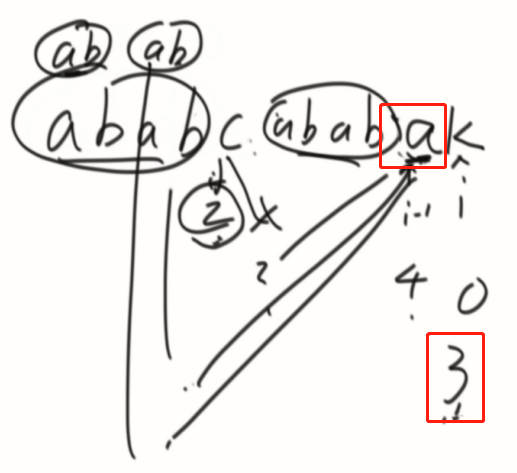
分析代码....
public class Code_01_KMP {
public static int getIndexOf(String s, String m) {
if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
return -1;
}
char[] ss = s.toCharArray();
char[] ms = m.toCharArray();
//匹配下标
int i1 = 0;
int i2 = 0;
int[] next = getNextArray(ms);
while (i1 < ss.length && i2 < ms.length) {
if (ss[i1] == ms[i2]) {
i1++;
i2++;
} else if (next[i2] == -1) {//-1标志数组第一个字符
i1++;//开头都配不上,就++
} else {
i2 = next[i2];//根据next的指引,往前跳,继续比对
}
}
return i2 == ms.length ? i1 - i2 : -1;
}
public static int[] getNextArray(char[] str2) {
if (str2.length == 1) {
return new int[] { -1 };
}
int[] next = new int[str2.length];
next[0] = -1;
next[1] = 0;
int pos = 2;
int cn = 0;//跳到的位置
while (pos < next.length) {
if (str2[pos - 1] == str2[cn]) {
next[pos++] = ++cn;
} else if (cn > 0) {
cn = next[cn];
} else {
next[pos++] = 0;
}
}
return next;
}
public static void main(String[] args) {
String str = "abcabcababaccc";
String match = "ababa";
System.out.println(getIndexOf(str, match));
}
}
KMP应用。
2017秋招京东原题:
输出包含两次原子串的最短字符串
例如:
输入:aba
输出:ababa
计算输入字符的next数组,计算到最后一个位置,看看前面有多少是已经叠加复用的,不够再往后添加上字符。
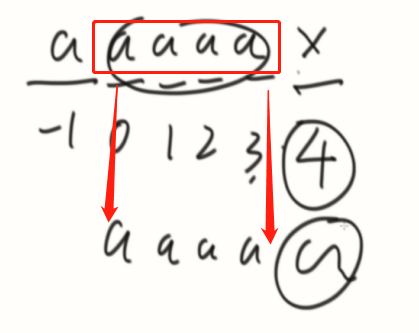
public class Code_02_KMP_ShortestHaveTwice {
public static String answer(String str) {
if (str == null || str.length() == 0) {
return "";
}
char[] chas = str.toCharArray();
if (chas.length == 1) {
return str + str;
}
if (chas.length == 2) {
return chas[0] == chas[1] ? (str + String.valueOf(chas[0])) : (str + str);
}
int endNext = endNextLength(chas);
//该子字符串始于指定索引处的字符,一直到此字符串末尾。
return str + str.substring(endNext);
}
public static int endNextLength(char[] chas) {
int[] next = new int[chas.length + 1];
next[0] = -1;
next[1] = 0;
int pos = 2;
int cn = 0;
while (pos < next.length) {
if (chas[pos - 1] == chas[cn]) {
next[pos++] = ++cn;
} else if (cn > 0) {
cn = next[cn];
} else {
next[pos++] = 0;
}
}
return next[next.length - 1];
}
public static void main(String[] args) {
String test1 = "a";
System.out.println(answer(test1));
String test2 = "aa";
System.out.println(answer(test2));
String test3 = "ab";
System.out.println(answer(test3));
String test4 = "abcdabcd";
System.out.println(answer(test4));
String test5 = "abracadabra";
System.out.println(answer(test5));
}
}
题目二:
在T1中找是否包含T2子树。
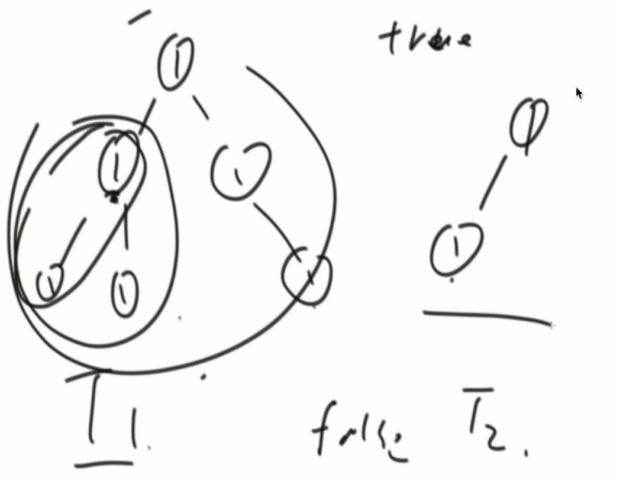
把T1和T2都序列化为串,判断是否为子串。
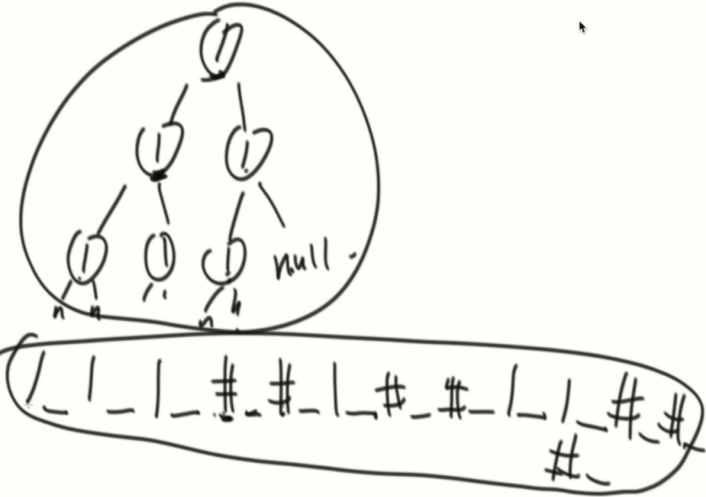
public class Code_03_KMP_T1SubtreeEqualsT2 {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static boolean isSubtree(Node t1, Node t2) {
String t1Str = serialByPre(t1);
String t2Str = serialByPre(t2);
return getIndexOf(t1Str, t2Str) != -1;
}
public static String serialByPre(Node head) {
if (head == null) {
return "#!";
}
String res = head.value + "!";
res += serialByPre(head.left);
res += serialByPre(head.right);
return res;
}
// KMP
public static int getIndexOf(String s, String m) {
if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
return -1;
}
char[] ss = s.toCharArray();
char[] ms = m.toCharArray();
int[] nextArr = getNextArray(ms);
int index = 0;
int mi = 0;
while (index < ss.length && mi < ms.length) {
if (ss[index] == ms[mi]) {
index++;
mi++;
} else if (nextArr[mi] == -1) {
index++;
} else {
mi = nextArr[mi];
}
}
return mi == ms.length ? index - mi : -1;
}
public static int[] getNextArray(char[] ms) {
if (ms.length == 1) {
return new int[] { -1 };
}
int[] nextArr = new int[ms.length];
nextArr[0] = -1;
nextArr[1] = 0;
int pos = 2;
int cn = 0;
while (pos < nextArr.length) {
if (ms[pos - 1] == ms[cn]) {
nextArr[pos++] = ++cn;
} else if (cn > 0) {
cn = nextArr[cn];
} else {
nextArr[pos++] = 0;
}
}
return nextArr;
}
public static void main(String[] args) {
Node t1 = new Node(1);
t1.left = new Node(2);
t1.right = new Node(3);
t1.left.left = new Node(4);
t1.left.right = new Node(5);
t1.right.left = new Node(6);
t1.right.right = new Node(7);
t1.left.left.right = new Node(8);
t1.left.right.left = new Node(9);
Node t2 = new Node(2);
t2.left = new Node(4);
t2.left.right = new Node(8);
t2.right = new Node(5);
t2.right.left = new Node(9);
System.out.println(isSubtree(t1, t2));
}
}
题目三:
怎么判断一个字符串,不是由一个子字符串得到的。
123123123123、aabaabaabaabaab
KMP的应用,最后的结束位的前缀和后缀,会呈整数倍的关系。每次划分位置都是相等的整数倍。
KMP要好好消化。
二、Manacher算法详解与应用
最长回文子串。
暴力方式:o(n²)
全部加上#后,逐个计算回文(通过从当前字符每次比对临近左右两个数来计算),取出最大的回文数再除以2即答案。

概念建设:
1、回文半径数组(存放每个位置对应的回文半径)
2、回文最右边界。(实际字符串有虚轴#)
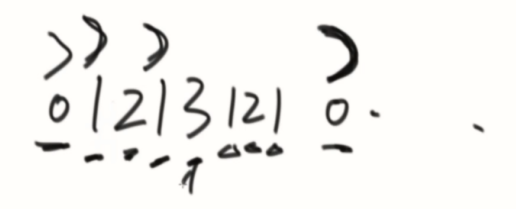
3、回文最右边界的中心
可能性:
1、不在最右边界里面,暴力扩充就行。
2、3、4是i在右边界里面的情况扩充。
2、i的回文半径在右边界里面。
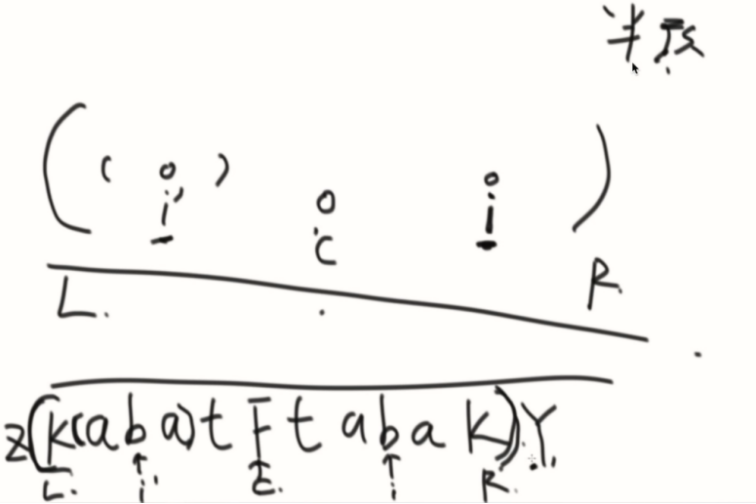
这种情况i不用计算,直接和i’一样。
证明:
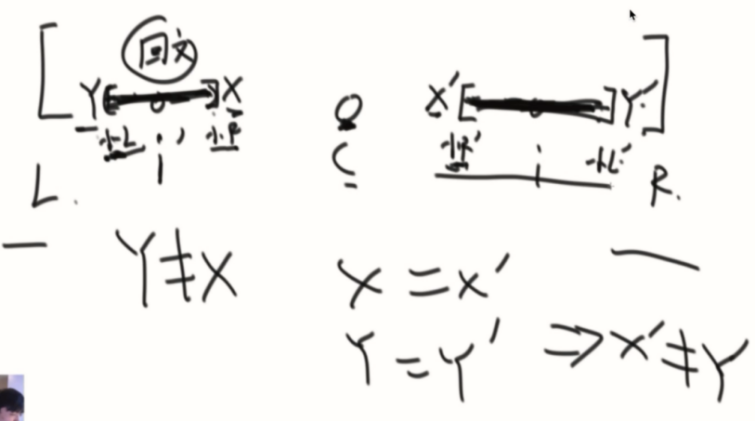
3、左边界没扩住i’的情况。i的回文半径是i~R
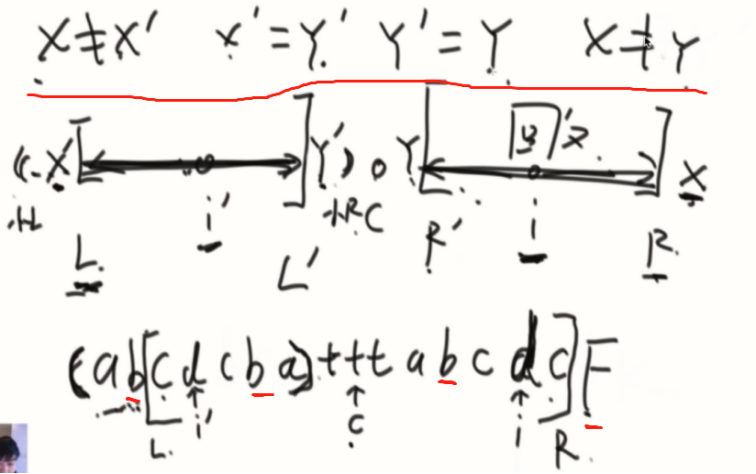
4、与L压线
从i~R是不用验证的,过了R之后还是要继续扩充验证。
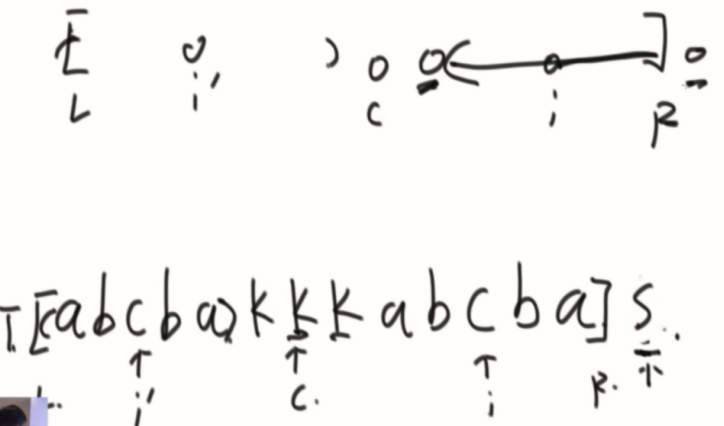
复杂度

再画一下各种情况
i在R内部。
①在内,直接等于i’的
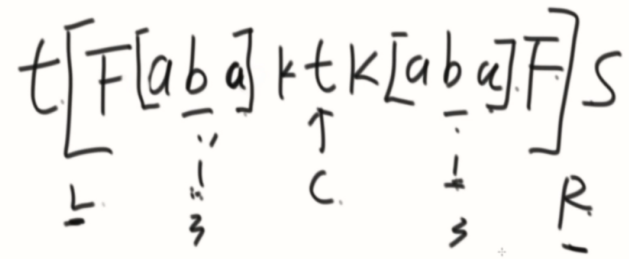
②L外,i~R
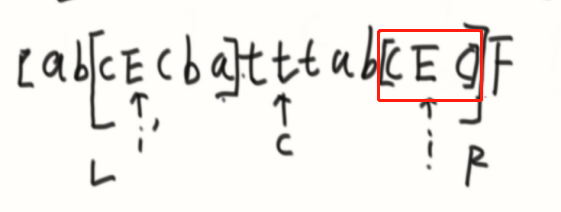
③压线,要继续向外扩充判断。
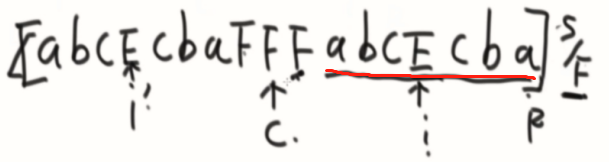
public class Code_04_Manacher {
public static char[] manacherString(String str) {
char[] charArr = str.toCharArray();
char[] res = new char[str.length() * 2 + 1];
int index = 0;
for (int i = 0; i != res.length; i++) {
res[i] = (i & 1) == 0 ? '#' : charArr[index++];
}
return res;
}
public static int maxLcpsLength(String str) {
if (str == null || str.length() == 0) {
return 0;
}
char[] charArr = manacherString(str);
//回文半径数组
int[] pArr = new int[charArr.length];
int C = -1;
int R = -1;
int max = Integer.MIN_VALUE;
for (int i = 0; i != charArr.length; i++) {
//i'的回文和i~R的距离,谁更近就是i的瓶颈
//2 * C - i --> i'的位置
//pArr[2 * C - i] i'的回文半径
//R - i --> i到R的距离
//R > i i在R的边界里面
pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
//全部情况都往外扩,虽然情况2、3扩充一次后会直接失败,但统一简化了代码
//检查是否越界
while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
pArr[i]++;
else {
break;
}
}
//如果扩充区域超过了R,做相应的更新
if (i + pArr[i] > R) {
R = i + pArr[i];
C = i;
}
//记录全局最大值
max = Math.max(max, pArr[i]);
}
return max - 1;
}
public static void main(String[] args) {
String str1 = "abc1234321ab";
System.out.println(maxLcpsLength(str1));
}
}
应用:如果只能在字符串最后添加字符,怎么让字符成为回文字符串?要求添加字符最少。
思路:就是在求必须包含最后一个字符串的情况下,最长回文串是多少,前面不是的部分逆序过来添上去。
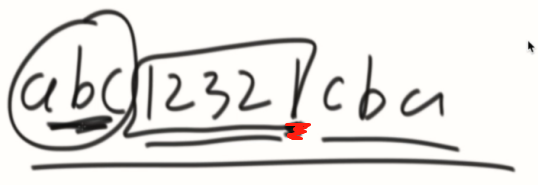
改写Manacher:
获得第一个达到最后边界的位置,知道了LR边界,把L边界前面的逆序,添加到总体字符串的后面,既是答案。

例子:
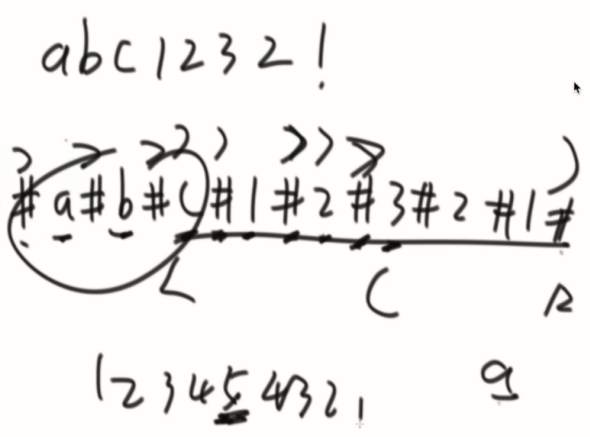
加#解决偶回文的问题

public class Code_05_Manacher_ShortestEnd {
public static char[] manacherString(String str) {
char[] charArr = str.toCharArray();
char[] res = new char[str.length() * 2 + 1];
int index = 0;
for (int i = 0; i != res.length; i++) {
res[i] = (i & 1) == 0 ? '#' : charArr[index++];
}
return res;
}
public static String shortestEnd(String str) {
if (str == null || str.length() == 0) {
return null;
}
char[] charArr = manacherString(str);
int[] pArr = new int[charArr.length];
int index = -1;
int pR = -1;
int maxContainsEnd = -1;
for (int i = 0; i != charArr.length; i++) {
pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;
while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
pArr[i]++;
else {
break;
}
}
if (i + pArr[i] > pR) {
pR = i + pArr[i];
index = i;
}
if (pR == charArr.length) {
maxContainsEnd = pArr[i];
break;
}
}
//原串 - 回文串 + 1 = 后补的长度
char[] res = new char[str.length() - maxContainsEnd + 1];
for (int i = 0; i < res.length; i++) {
res[res.length - 1 - i] = charArr[i * 2 + 1];
}
return String.valueOf(res);
}
public static void main(String[] args) {
String str2 = "abcd123321";
System.out.println(shortestEnd(str2));
}
}
要多练练,算法相伴随的衍生题目,提高敏感度。
代码解读:
取最近距离。

I’在区域内的情况:
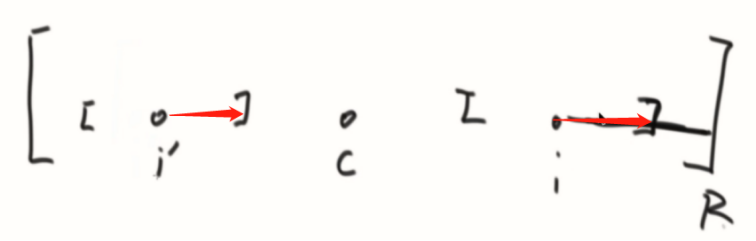
I’在区域外的情况:
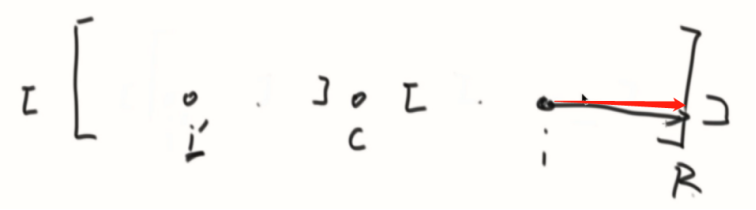
算法进阶面试题01——KMP算法详解、输出含两次原子串的最短串、判断T1是否包含T2子树、Manacher算法详解、使字符串成为最短回文串的更多相关文章
- leetcode.字符串.125验证回文串-Java
1. 具体题目 给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写.说明:本题中,我们将空字符串定义为有效的回文串. 示例 1: 输入: "A man, a pl ...
- 37:密码截取(回文串manacher算法)
题目描述:Catcher是MCA国的情报员,他工作时发现敌国会用一些对称的密码进行通信,比如像这些ABBA,ABA,A,123321,但是他们有时会在开始或结束时加入一些无关的字符以防止别国破解.比如 ...
- UVA 11584 Partitioning by Palindromes 划分回文串 (Manacher算法)
d[i]表示前面i个字符划分成的最小回文串个数, 转移:当第i字符加进来和前面区间j构成回文串,那么d[i] = d[j]+1. 要判断前面的字符j+1到i是不是回文串,可以用Manacher算法预处 ...
- 【BZOJ2565】最长双回文串 (Manacher算法)
题目: BZOJ2565 分析: 首先看到回文串,肯定能想到Manacher算法.下文中字符串\(s\)是输入的字符串\(str\)在Manacher算法中添加了字符'#'后的字符串 (构造方式如下) ...
- hdu 3068 最长回文 (Manacher算法求最长回文串)
参考博客:Manacher算法--O(n)回文子串算法 - xuanflyer - 博客频道 - CSDN.NET 从队友那里听来的一个算法,O(N)求得每个中心延伸的回文长度.这个算法好像比较偏门, ...
- 力扣算法:125-验证回文串,131-分割回文串---js
LC 125-验证回文串 给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写. 说明:本题中,我们将空字符串定义为有效的回文串. 注:回文串是正着读和反着读都一样的字符串. ...
- manacher算法,求回文串
用来求字符串最长回文串或者回文串的总数量 #include<map> #include<queue> #include<stack> #include<cma ...
- 【bzoj3676】[Apio2014]回文串 —— 回文自动机的学习
写题遇上一棘手的题,[Apio2014]回文串,一眼看过后缀数组+Manacher.然后就码码码...过是过了,然后看一下[Status],怎么慢这么多,不服..然后就搜了一下,发现一种新东西——回文 ...
- 【回文串-Manacher】
Manacher算法能够在O(N)的时间复杂度内得到一个字符串以任意位置为中心的回文子串.其算法的基本原理就是利用已知回文串的左半部分来推导右半部分. 转:http://blog.sina.com.c ...
随机推荐
- windws 下 sublime Text 3 ·安装的安装与激活
下载sublime 我们可以到官网进行下载对应的版本 https://www.sublimetext.com/3 如下是官网的内容(我选择的是Windows 64 bit). Sublime Text ...
- L-BFGS算法(转载)
转载链接:http://blog.csdn.net/itplus/article/details/21897715 前面的拟牛顿法.DFP.BFGS.L-BFGS算法简短总结一下就是: 牛顿法不仅使用 ...
- word打不开怎么办?
方法一 故障描述:编辑Word文档的过程中,程序非法关闭,重新打开也是如此.即使重新安装了Office 2003,在启动Word 2003后仍然出现了异常情况.双击Word文档后,程序弹出出错对话框, ...
- n个随机变量中第k小值的期望
Problem 有\(n\)个相互独立的取值在\([0,1]\)的随机变量,问其中第\(k\)小的变量期望是多少? Solution 之前pkuwc的神仙找我换友链,让我受宠若惊.. 我今天突然翻到他 ...
- zabbix3.0.4导入中文模板后乱码问题处理
通过yum安装方式部署了zabbix3.0.4监控服务器,配置过程中发现当导入的模板中有中文时,图中的中文会变成方块 如下图所示: 这个问题是由于zabbix的web端没有中文字库,我们最需要把中文字 ...
- FreeSWITCH IVR中lua调用并执行nodejs代码
一.功能需求: 通过FreeSWITCH的IVR按键调用相应的脚本文件:nodejs提供很多的模组,可以方便的与其它系统或者进行任何形式的通讯,我的应用是通过nodejs发送http post请求: ...
- Eclipse开发时出现HTTP 403 错误(禁止访问)的解决方法
1. 打开项目的页面如下: 可以从tomcat log中发现Connection has been abandoned PooledConnection和Too many connections. 2 ...
- python中的zip、map、reduce 、lambda函数的使用。
lambda只是一个表达式,函数体比def简单很多. lambda的主体是一个表达式,而不是一个代码块.仅仅能在lambda表达式中封装有限的逻辑进去. lambda表达式是起到一个函数速写的作用.允 ...
- 笔记 oracle 创建联合主键
笔记 alter table tablename add constraint unionkeyname primary key (column1,column2); 上面语句中: tablename ...
- linux POSIX 信号量介绍
信号量一.什么是信号量信号量的使用主要是用来保护共享资源,使得资源在一个时刻只有一个进程(线程)使用.多线程可以同时运行多个线程函数完成功能,但是对于共享数据如果不加以锁定,随意改变共享数据的值会发生 ...
