【LeetCode每天一题】Fibonacci Number(斐波那契数列)

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0,   F(1) = 1                          F(N) = F(N - 1) + F(N - 2), for N > 1.

Given N, calculate F(N).

Example 1:            Input: 2            Output: 1                 Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:            Input: 3            Output: 2                 Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:            Input: 4            Output: 3                 Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Note:                0 ≤ N ≤ 30.

解决思路： 这道题最简单的思路就是直接使用递归进行解决（从给定值往小计算），但是递归的过程存在很多重复计算。当题中N给的很大时，计算时间会加长。 因此采用从小到大的方式进行计算。

　　如果使用递归，则步骤图如下：

　                   　

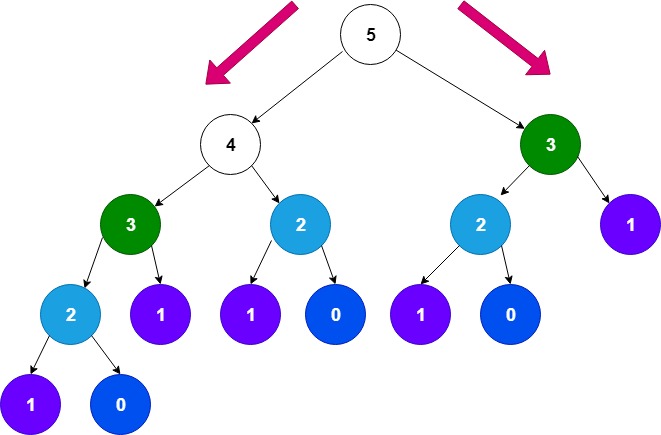
　　可以看到，有很多节点的值被重复计算了。

　　而如果从小到大步骤如下：（不会产生的多余的计算）

　　　             　

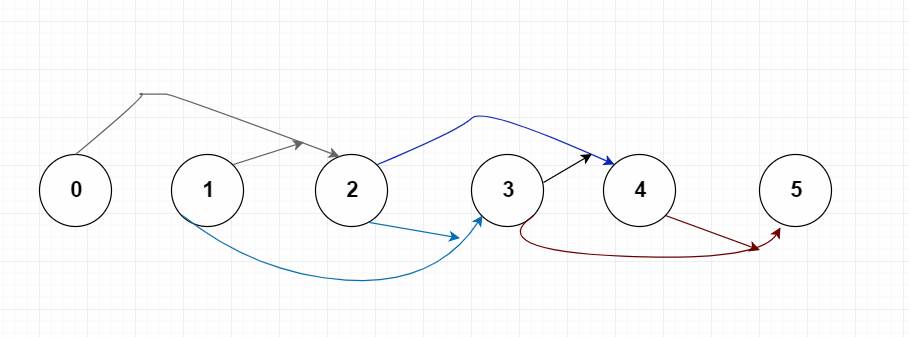
　　解决代码如下：时间复杂度为O(n), 空间复杂度为O(1)

 class Solution(object):
     def fib(self, N):
         """
         :type N: int
         :rtype: int
         """
         if N < :
             return
         if N ==  or N == :         # 当N为1 or  时， 直接返回。
             return  if N ==  else
         one, two = ,
         for i in range(N-):    # 进行计算
             one, two = two, one+two
         return two