图论篇2——最小生成树算法（kurskal算法&prim算法）

基本概念

树（Tree）

如果一个无向连通图中不存在回路，则这种图称为树。

生成树 （Spanning Tree）

无向连通图G的一个子图如果是一颗包含G的所有顶点的树，则该子图称为G的生成树。

生成树是连通图的极小连通子图。这里所谓极小是指：若在树中任意增加一条边，则将出现一条回路；若去掉一条边，将会使之变成非连通图。

最小生成树

一个带权值的连通图。用$n-1$条边把$n$个顶点连接起来，且连接起来的权值最小。

应用场景

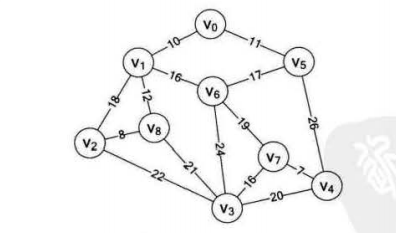
设想有9个村庄，这些村庄构成如下图所示的地理位置，每个村庄的直线距离都不一样。若要在每个村庄间架设网络线缆，若要保证成本最小，则需要选择一条能够联通9个村庄，且长度最小的路线。

Kruskal算法

知识点：数据结构——并查集

基本思想

始终选择当前可用、不会（和已经选取的边）构成回路的最小权植边。

具体步骤：

1. 将所有边按权值进行降序排序

2. 依次选择权值最小的边

3. 若该边的两个顶点落在不同的连通分量上，选择这条边，并把这两个顶点标记为同一连通分量；若这条边的两个顶点落到同一连通分量上，舍弃这条边。反复执行2,3，直到所有的都在同一连通分量上。【这一步需要用到上面的并查集】

模板题：https://www.luogu.org/problem/P3366

#include <iostream>
#include <algorithm>
using namespace std;
int pre[];
int n, m; //n个定点，m条边
 
struct ENode {
    int from, to, dis;
    bool operator<(ENode p) {
        return dis < p.dis;
    }
}M[];
 
int Find(int x) {
    return x == pre[x] ? pre[x] : pre[x] = Find(pre[x]);
}
 
int kurskal() {
    sort(M, M + m);
    int N = n, res = ;
    for (int i = ; i < m && N > ; i++) {
        int fx = Find(M[i].from), fy = Find(M[i].to);
        if (fx != fy) {
            pre[fx] = fy;
            N--;//找到了一条边，当N减到1的时候表明已经找到N-1条边了，就完成了
            res += M[i].dis;
        }
    }
    if (N == )//循环做完，N不等于1 表明没有找到合适的N-1条边来构成最小生成树
        return res;
    return -;
}
 
int main() {
    cin >> n >> m;
    for (int i = ; i <= n; i++) {
        pre[i] = i;
    }
    for (int i = ; i < m; i++) {
        scanf("%d%d%d", &M[i].from, &M[i].to, &M[i].dis);;
    }
    int ans = kurskal();
    if (ans != -)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return ;
}

Prim算法

Prim算法思想：

首先将图的点分为两部分，一种是访问过的$u$（第一条边任选），一种是没有访问过的$v$

1: 每次找$u$到$v$的权值最小的边。

2: 然后将这条边中的$v$中的顶点添加到$u$中，直到$v$中边的个数$=$顶点数$-1$

图解步骤：

维护一个$dis$数组，记录只使用已访问节点能够到达各未访问节点最短的权值。

初始值为节点1（任意一个都可以）到各点的值，规定到自己是0，到不了的是$inf$（定义一个特别大的数）。

找当前能到达的权值最短的点。1-->4，节点4

将dis[4]赋值为0，标记为已访问过，同时借助4节点更新dis数组。

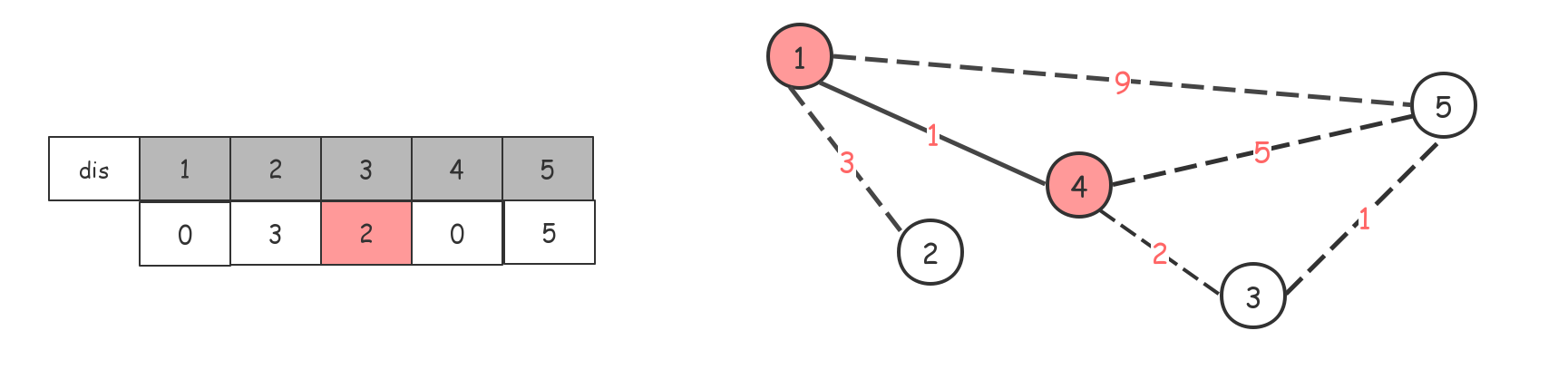
后面依次

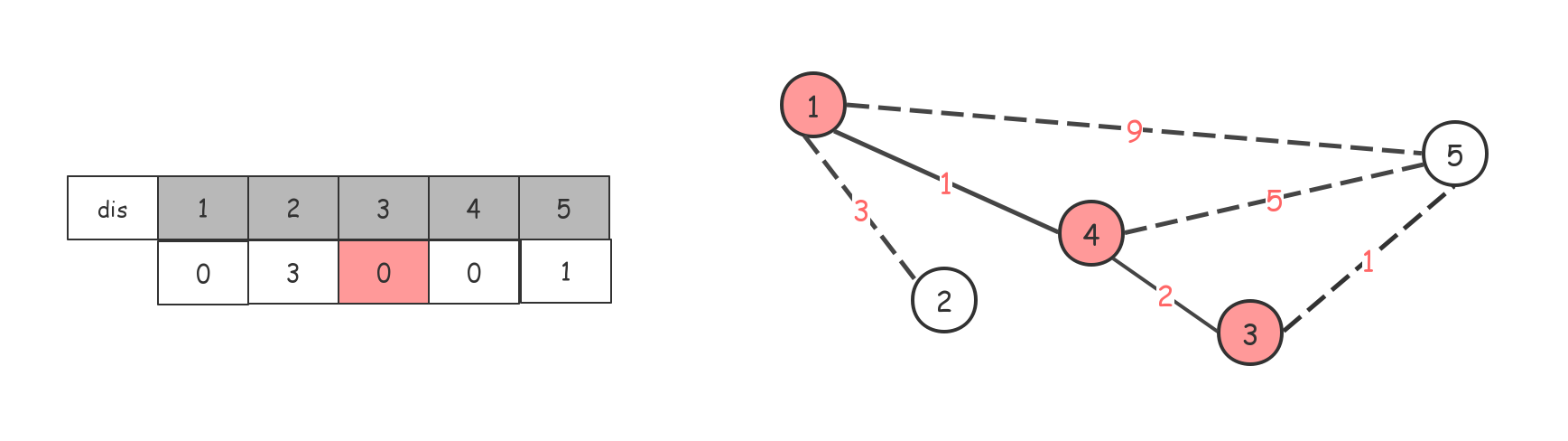
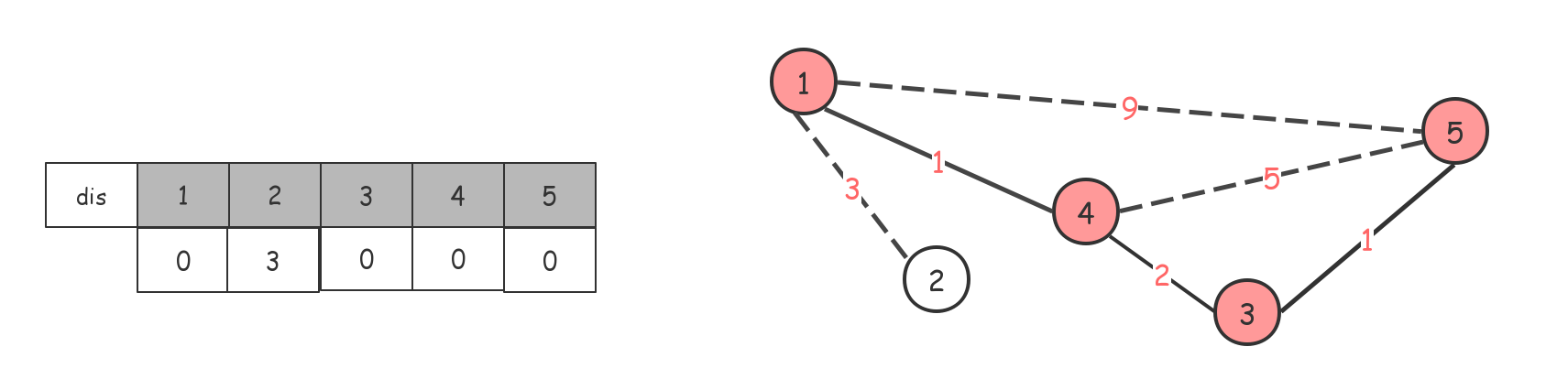
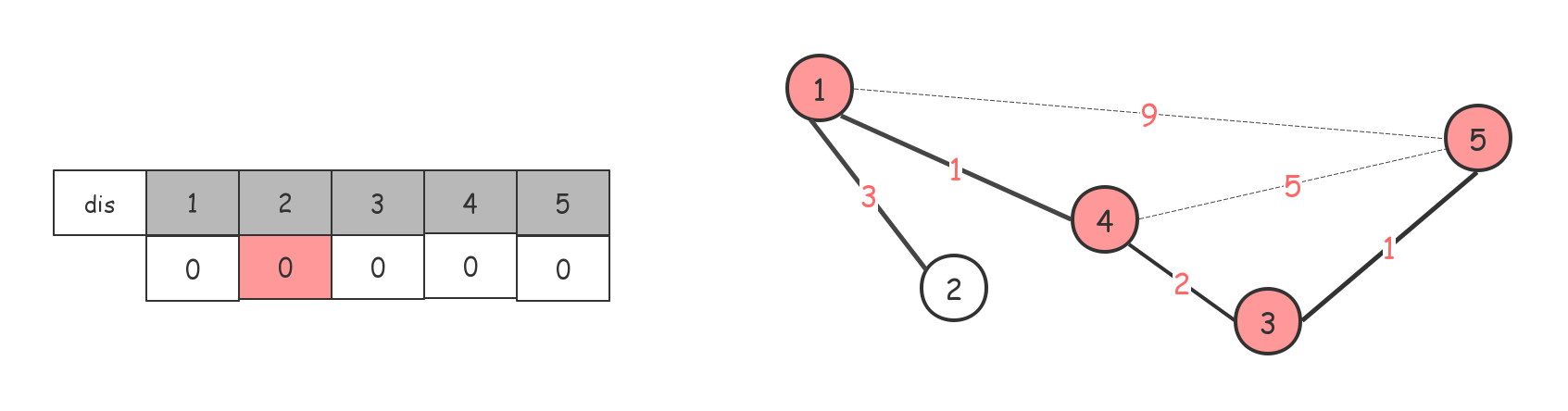
最后整个dis数组都是0了，最小生成树也就出来了，如果$dis$数组中还有 $inf$ 的话，说明这不是一个连通图。

还是上面那道模板题：https://www.luogu.org/problem/P3366

#include <iostream>
 
#include <fstream>
using namespace std;
 
struct ENode {
    int dis, to;//权重、指向
    ENode* next = NULL;
    void push(int to, int dis) {
        ENode* p = new ENode;
        p->to = to; p->dis = dis;
        p->next = next;
        next = p;
    }
}*head;
const int inf =  << ;
int N, M;
int dis[];
 
int prim() {
    int res = ;
 
    for (int i = ; i <= N; i++) {
        dis[i] = inf;
    }
 
    for (int i = ; i < N; i++) {//与kurskal区分，找边是N-1条边，找点是N个点
        int v =  , MIN = inf;
        for (int j = ; j <= N; j++) {
            //到不了的，访问过的不进行比较
            if (dis[j] !=  && dis[j] < MIN) {
                v = j;
                MIN = dis[j];
            }
        }
        if (MIN == inf && v != )//这里v!=1是为了把dis的初始化放在循环里面做，也可以放在循环外面做，但是外层循环就只需要做N-1次了
            return -;//还没找够n个点，没路了
        res += dis[v];
        dis[v] = ;
        ENode *p = head[v].next;
        while (p) {
            if (dis[p->to] > p->dis) {
                dis[p->to] = p->dis;
            }
            p = p->next;
        }
    }
    return res;
}
 
int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL
 
    cin >> N >> M;
    head = new ENode[N + ];
    for (int i = ; i < M; i++) {
        int from, to, dis;
        scanf("%d%d%d", &from, &to, &dis);
        //cin >> from >> to >> dis;
        head[from].push(to, dis);
        head[to].push(from, dis);
    }
    int ans = prim();
    if (ans != -)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return ;
}

两者区别

时间复杂度

prim算法

时间复杂度为$O(n^2)$，$n$为顶点的数量，其时间复杂度与边得数目无关，适合稠密图。

kruskal算法

时间复杂度为$O(e\cdot loge)$，$e$为边的数目，与顶点数量无关，适合稀疏图。

其实就是排序的时间，因为并查集的查询、合并操作都是$O(1)$。

总结

通俗点说就是，点多边少用Kruskal，因为Kruskal算法每次查找最短的边。 点少边多用Prim，因为它是每次找一个顶点。

具体选择用那个，可以用电脑算一下，题目给的数据级别，$n^2$和$e\cdot loge$看看那个小，比如上面的模板题，题目给的数据级别是$(n<=5000,e<=200000)$，粗略估算一下，kurskal算法一定是会快不少的，结果也确实如粗。

实现难度

明眼人都能看出来，kurskal算法要简单太多了。kurskal算法不需要把图表示出来，而Prim算法必须建表或者邻接矩阵，所以从上面的数据也能看出来当边的数目较大时，Prim算法所占用的空间比kurskal算法多了很多。

拓展

堆优化Prim算法

用堆存储当前所有可到达的点和距离，就是把dis数组里的内容一式两份，存在堆里，然后每次取堆顶元素，每次操作为$O(logn)$，所以使用堆优化后的Prim算法理论上时间复杂度为$O(nlogn)$，但是好像没有达到想要的效果

看了测试数据发现，有很多重边，那就合理了，做了很多次的无用循环，所以时间上也和kurskal比较相近。所以在数据可靠、无重边的情况下，这个算法一定是上述几种中最快的一个。

#include <iostream>
#include <fstream>
#include <cstdio>
#include <queue>
 
using namespace std;
struct P {
    int dis, v;
    P(int d, int v) :dis(d), v(v) {};
    bool operator<(P p)const {
        return p.dis < dis;
    }
};
struct ENode {
    int dis, to;//权重、指向
    ENode* next = NULL;
    void push(int to, int dis) {
        ENode* p = new ENode;
        p->to = to; p->dis = dis;
        p->next = next;
        next = p;
    }
}*head;
const int inf =  << ;
int N, M;
int dis[];
bool fuck[];
 
int prim() {
    priority_queue<P>pq;
    pq.push(P(, ));
    int res = , cnt = N;
    dis[] = ;
    fill(dis + , dis + N + , inf);
 
    while (!pq.empty() && cnt > ) {//与kurskal区分，找边是N-1条边，找点是N个点
        int v = pq.top().v, d = pq.top().dis;
        pq.pop();
        if (fuck[v])continue;
        fuck[v] = true;
        res += d;
        cnt--;
        ENode* p = head[v].next;
        while (p) {
            if (dis[p->to] > p->dis) {
                dis[p->to] = p->dis;
                pq.push(P(p->dis, p->to));
            }
            p = p->next;
        }
    }
    if (cnt > )
        return -;
    return res;
}
 
int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL
    cin >> N >> M;
    head = new ENode[N + ];
    for (int i = ; i < M; i++) {
        int from, to, dis;
        scanf("%d%d%d", &from, &to, &dis);
        //cin >> from >> to >> dis;
        head[from].push(to, dis);
        head[to].push(from, dis);
    }
    int ans = prim();
    if (ans != -)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return ;
}