3486 ( Interviewe )RMQ

Problem Description

YaoYao has a company and he wants to employ m people recently. Since his company is so famous, there are n people coming for the interview. However, YaoYao is so busy that he has no time to interview them by himself. So he decides to select exact m interviewers for this task.
YaoYao decides to make the interview as follows. First he queues the interviewees according to their coming order. Then he cuts the queue into m segments. The length of each segment is 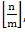, which means he ignores the rest interviewees (poor guys because they comes late). Then, each segment is assigned to an interviewer and the interviewer chooses the best one from them as the employee.
YaoYao’s idea seems to be wonderful, but he meets another problem. He values the ability of the ith arrived interviewee as a number from 0 to 1000. Of course, the better one is, the higher ability value one has. He wants his employees good enough, so the sum of the ability values of his employees must exceed his target k (exceed means strictly large than). On the other hand, he wants to employ as less people as possible because of the high salary nowadays. Could you help him to find the smallest m?

 

Input

The input consists of multiple cases.
In the first line of each case, there are two numbers n and k, indicating the number of the original people and the sum of the ability values of employees YaoYao wants to hire (n≤200000, k≤1000000000). In the second line, there are n numbers v1, v2, …, vn (each number is between 0 and 1000), indicating the ability value of each arrived interviewee respectively.
The input ends up with two negative numbers, which should not be processed as a case.

 

Output

For each test case, print only one number indicating the smallest m you can find. If you can’t find any, output -1 instead.

 

Sample Input

11 300
7 100 7 101 100 100 9 100 100 110 110
-1 -1

 

Sample Output

3

Hint

We need 3 interviewers to help YaoYao. The first one interviews people from 1 to 3, the second interviews people from 4 to 6,
and the third interviews people from 7 to 9. And the people left will be ignored. And the total value you can get is 100+101+100=301>300.

 

Source

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU

 

Recommend

zhengfeng   |   We have carefully selected several similar problems for you:  2586 2874 2888 3478 3487 

题解 ： RMQ

C++代码：

#include<iostream>
#include<cstdio>
#include<string>
#include<cmath>
#include<cstring>
using namespace std;
#define MAXN 200000 +9
#define MAXE 22
int h[MAXN],mmax[MAXN][MAXE];
int N,Q;
int L,R;
void RMQ_ST(){
    for(int i=;i<=N;i++){
        mmax[i][]=h[i];

    }
    int end_j=log(N+0.0)/log(2.0);
    int end_i;
    for(int j=;j<=end_j;j++){
        end_i=N+-(<<j);
        for(int i=;i<=end_i;i++){
            mmax[i][j]=max(mmax[i][j-],mmax[i+(<<(j-))][j-]);
           // mmin[i][j]=min(mmin[i][j-1],mmin[i+(1<<(j-1))][j-1]);
        }
    }
}
int QueryMax(int L,int R){

    int k=log(R-L+1.0)/log(2.0);
    return max(mmax[L][k],mmax[R-(<<k)+][k]);
}

int main(){
    while(~scanf("%d%d",&N,&Q)&&(N >  || Q > )){
        int maxx = ;
        for(int i=;i<=N;i++){
            scanf("%d",&h[i]);
            maxx = max(h[i],maxx);
        }
        int m = ;

        RMQ_ST();
        m = Q / maxx;

        int flag = ;
        if(m == ) {
            m = ;
            flag = ;
            goto out ;
        }
        for(;m <= N; m ++){
            int res = ;
            int sss = ;

            int s = N / m;
            int i = ;
            int j = m;
            while(j--){
                res += QueryMax(i ,i + s-  );
                i += s;
            }
            if(res > Q) {
                flag = ;
                break;
                }
        }
        out :
        if(!flag) printf("-1\n");
        else
            cout << m << endl;

   }

return ;
}