[CSP-S模拟测试]:世界线(DFS+bitset)
题目描述
时间并不是一条单一的线,而是有许多世界线构成的流。
在一些时刻,世界线会发生分裂;同样的,它们也有可能在一些时刻收束在一起。如果将这些时刻抽象成点,那么这些世界线构成的网络,实际上是一张有向无环图。
$Okabe$想要改变世界线的构造,他认为世线是优美的,当且仅当其中不存在三个点$u,v,t$,其中$u$到$v$有连边,$v$到$t$有连边,而$u$到$t$没有连边。
作为世界的观测者,$Okabe$已经知道了世界线的构成。现在他想知道,在不删边的情况下,至少要连接多少条边,才能得到优美的世界线。
输入格式
第一行两个整数$n,m$,表示点数和边数。
接下来$m$行,每行两个整数$n,m$,表示点数和边数。
接下来$m$行,每行两个整数$u,v$,表示$u$到$v$有一条有向边。
输出格式
仅包含一个整数,表示答案。
样例
样例输入:
5 5
1 2
1 3
2 3
3 4
4 5
样例输出:
5
数据范围与提示
样例解释:
还需要连边$(1,4),(1,5),(2,4),(2,5),(3,5)$。
数据范围:
保证$1\leqslant u,v\leqslant n$,给出的图是一张有向无环图,且没有重边和自环。
各个测试点还满足如下约束:

题解
先来明确题意,一个点如果是另一个点的父亲,那么也一定是那个点的爷爷,如下图:
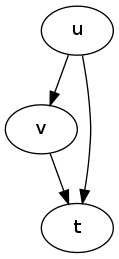
那么我们需要连边的数量就是每个点的祖先数$-1$,为什么呢?再来看一张图:
 $\rightarrow$
$\rightarrow$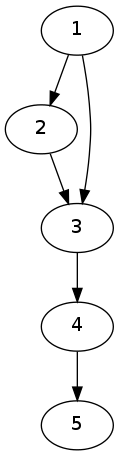 $\rightarrow$
$\rightarrow$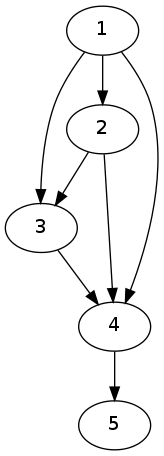 $\rightarrow$
$\rightarrow$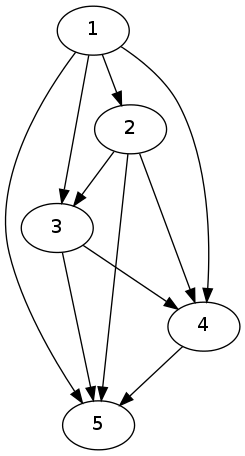
通过上面这四张图,我们发现,每个点都需要向除了它的直接父亲的所有点有连边。
那么对于$n=m-1$就已经轻松解决了。
但是你会发现样例还是过不了,我们先来看一下样例的图:
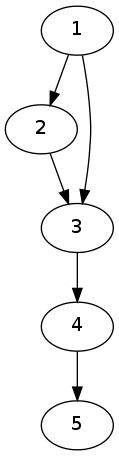
我们发现,对于点$3$,从$1$有两条路径可以到达$1$,那么我们考虑如何去重。
最朴素的做法就是记录一下所有祖先,但是这步操作可以$bitset$优化。
没错,这就是正解。
需要注意的是空间问题,分两次操作,第一次考虑前$30000$个点,第二次考虑后$30000$个点即可。
时间复杂度:$\Theta(\frac{n(n+m)}{w})$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;}e[100001];
int head[60001],cnt;
int n,m;
int du[60001],rd[60001];
int lft,rht;
int now,won,dp[2][60001],pos;
bitset<30001> bit[60001];
int ans,sum;
void add(int x,int y)
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void work(int x)
{
for(int i=head[x];i;i=e[i].nxt)
{
bit[e[i].to]|=bit[x];
du[e[i].to]--;
if(!du[e[i].to])
{
dp[!pos][++won]=e[i].to;
sum--;
ans+=bit[e[i].to].count();
}
}
}
void judge()
{
now=0,sum=n;
for(int i=1;i<=n;i++)du[i]=rd[i];
for(int i=1;i<=n;i++)
if(!du[i])
{
dp[0][++now]=i;
sum--;
if(lft<=i&&i<=rht)ans++;
}
pos=0;
while(sum)
{
won=0;
for(int i=1;i<=now;i++)work(dp[pos][i]);
pos^=1;
now=won;
}
}
void check()
{
for(int i=1;i<=n;i++)bit[i].reset();
for(int i=lft;i<=min(n,rht);i++)bit[i].set(i-lft);
judge();
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
du[y]++;
}
for(int i=1;i<=n;i++)rd[i]=du[i];
lft=1;
rht=30000;
while(lft<=n)
{
check();
lft+=30000;
rht+=30000;
}
printf("%d",ans-n-m);
return 0;
}
rp++
[CSP-S模拟测试]:世界线(DFS+bitset)的更多相关文章
- [考试反思]1109csp-s模拟测试106:撞词
(撞哈希了用了模拟测试28的词,所以这次就叫撞词吧) 蓝色的0... 蓝色的0... 都该联赛了还能CE呢... 考试结束前15分钟左右,期望得分300 然后对拍发现T2伪了写了一个能拿90分的垃圾随 ...
- [考试反思]1003csp-s模拟测试58:沉淀
稳住阵脚. 还可以. 至少想拿到的分都拿到了,最后一题的确因为不会按秩合并和线段树分治而想不出来. 对拍了,暴力都拍了.挺稳的. 但是其实也有波折,险些被卡内存. 如果内存使用不连续或申请的内存全部使 ...
- 2019.8.14 NOIP模拟测试21 反思总结
模拟测试20的还没改完先咕着 各种细节问题=错失190pts T1大约三分钟搞出了式子,迅速码完,T2写了一半的时候怕最后被卡评测滚去交了,然后右端点没有初始化为n…但是这样还有80pts,而我后来还 ...
- NOIP模拟测试19「count·dinner·chess」
反思: 我考得最炸的一次 怎么说呢?简单的两个题0分,稍难(我还不敢说难,肯定又有人喷我)42分 前10分钟看T1,不会,觉得不可做,完全不可做,把它跳了 最后10分钟看T1,发现一个有点用的性质,仍 ...
- NOIP模拟测试17&18
NOIP模拟测试17&18 17-T1 给定一个序列,选取其中一个闭区间,使得其中每个元素可以在重新排列后成为一个等比数列的子序列,问区间最长是? 特判比值为1的情况,预处理比值2~1000的 ...
- Android单元测试与模拟测试详解
测试与基本规范 为什么需要测试? 为了稳定性,能够明确的了解是否正确的完成开发. 更加易于维护,能够在修改代码后保证功能不被破坏. 集成一些工具,规范开发规范,使得代码更加稳定( 如通过 phabri ...
- [开源]微信在线信息模拟测试工具(基于Senparc.Weixin.MP开发)
目前为止似乎还没有看到过Web版的普通消息测试工具(除了官方针对高级接口的),现有的一些桌面版的几个测试工具也都是使用XML直接请求,非常不友好,我们来尝试做一个“面向对象”操作的测试工具. 测试工具 ...
- 安装nginx python uwsgi环境 以及模拟测试
uwsgi帮助文档: http://uwsgi-docs-cn.readthedocs.io/zh_CN/latest/WSGIquickstart.html http://uwsgi-docs.re ...
- 利用Python中的mock库对Python代码进行模拟测试
这篇文章主要介绍了利用Python中的mock库对Python代码进行模拟测试,mock库自从Python3.3依赖成为了Python的内置库,本文也等于介绍了该库的用法,需要的朋友可以参考下 ...
随机推荐
- LUOGU P3380 【模板】二逼平衡树(树套树)
传送门 解题思路 这里写的是常数巨大的线段树套\(splay\),卡了半天常才过.首先线段树每个节点挂一个\(splay\),\(splay\)中的元素即为线段树管辖的区间中的数.对于操作\(1\), ...
- Python实现BFS,DFS
BFS:队 graph = { "A" : ["B","C"], "B" : ["A"," ...
- 01 【零基础入门】html学习笔记(1)
之前学习了前端的一些基础知识,现在想深入地.精通地学习前端,往前端和全栈工程师方向发展. 之前学习前端主要是通过看视频,结合动手练习.现在认为看书+视频+实践,应该是最高效的学习方法.对于html.c ...
- 【ERP知识】一个VMI(供应商管理库存)实现方案
VMI,Vendor Managed Inventory,供应商管理库存 是指客户不采购或尽量少采购物料,而是由供应商保证该物料有充足的数量,在客户需要的时候能按时提供. 这样可以降低客户方的库存成本 ...
- 2018-2019-2 20175203 实验四《Android 开发基础》
20175203 2018-2019 实验四<Android 开发基础> 实验要求 参考Android开发简易教程 完成云班课中的检查点,也可以先完成实验报告,直接提交.注意不能只有截图, ...
- 阿里云使用ssl免费证书
购买免费证书 购买之后 申请证书 该域名必须添加一条TXT记录 根据提示添加记录 下载证书 我用的nginx做的映射,所以下载nginx nginx安装自行百度 将下载的文件解压到nginx目录下(创 ...
- 在阿里云 Ubuntu上通过nginx+uwsgi服务器部署Django出现的502错误
https://blog.csdn.net/luojie140/article/details/76919471 https://blog.csdn.net/sinat_21302587/articl ...
- Webshell免杀
过狗过D盾 <?php class me{ public $a = ''; function __destruct(){ assert("$this->a"); }}$ ...
- php的注释方法
注释是每个程序员学习时的基础,我们通过可以注释来备注一信息.增加代码的可读性.下面我们就为大家介绍一下PHP的注释方法. 1, // 这是单行注释 2,# 这也是单行注释 3,/* */多行注释块 ...
- 深度学习大规模MIMO中的功率分配
摘要-本文使用深度学习的方法在大规模MIMO网络的下行链路中执行max-min和max-prod功率分配.更确切地说,与传统的面向优化的方法相比,训练深度神经网络来学习用户设备(UE)的位置和最优功率 ...
