[CSP-S模拟测试]:表格（动态开点二维线段树+离散化）

题目传送门（内部题112）

---

输入格式

　　一个数$N$，表示矩形的个数。
　　接下来$N$行，每行四个整数$X_a,Y_a,X_b,Y_b$。分别表示每个矩形左下角和右上角的坐标。
　　保证$(X_a<X_b,Y_a<Y_b)$。

---

输出格式

　　一行，表示能看到的颜色数量。

---

样例

样例输入：

3
0 -1 1 1
2 1 3 5
-4 0 5 4

样例输出：

4

---

数据范围与提示

样例解释：

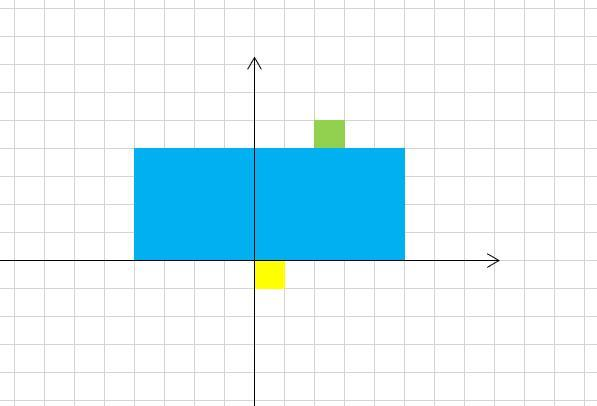
数据范围：

　　对于$10\%$的数据，保证$N\leqslant 100,|X_a,X_b,Y_a,Y_b|\leqslant 100$
　　对于$50\%$的数据，保证$N\leqslant 100,000,|X_a,X_b,Y_a,Y_b|\leqslant 1,000$
　　对于$80\%$的数据，保证$N\leqslant 100,000,|X_a,X_b,Y_a,Y_b|\leqslant 100,000$
　　对于$100\%$的数据，保证$N\leqslant 100,000,|X_a,X_b,Y_a,Y_b|\leqslant 10^9$

---

题解

其实$Ctrl+Z$是个提示。

然而我的考场代码……

愣是没有想到可以反着来。

反着来有一个很好的性质，就是如果这段已经被覆盖过了，那么现在插入的这个肯定是被压在下面的。

那么可以用二维线段树，存储哪个区间已经被覆盖了即可，如果有一段区间没有被覆盖，那么答案就$+1$即可。

注意离散化和动态开点即可。

随机数据下很优秀，但是极限数据会被卡，因为时间复杂度还是$\Theta(n^2)$的。

时间复杂度：$\Theta(n^2)$（但是可过）。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int xa,xb,ya,yb;}e[100001];
unordered_map<int,int> mpx,mpy;
int n;
int x[300001],y[300001],topx,topy,cntx,cnty;
int rt,tot,lson[60000000],rson[60000000];
bool tr[60000000];
int ans,res;
void pushup(int x){tr[x]=tr[lson[x]]&tr[rson[x]];}
void add(int &x,int xl,int yl,int xr,int yr,int opt,int XL,int YL,int XR,int YR)
{
	if(!x)x=++tot;
	if(tr[x]||xr<XL||XR<xl||yr<YL||YR<yl)return;
	if(XL<=xl&&xr<=XR&&YL<=yl&&yr<=YR)
	{
		tr[x]=1;
		ans+=res;
		res=0;
		return;
	}
	if(opt)
	{
		int mid=(xl+xr)>>1;
		add(lson[x],xl,yl,mid,yr,0,XL,YL,XR,YR);
		add(rson[x],mid+1,yl,xr,yr,0,XL,YL,XR,YR);
	}
	else
	{
		int mid=(yl+yr)>>1;
		add(lson[x],xl,yl,xr,mid,1,XL,YL,XR,YR);
		add(rson[x],xl,mid+1,xr,yr,1,XL,YL,XR,YR);
	}
	pushup(x);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d%d%d",&e[i].xa,&e[i].ya,&e[i].xb,&e[i].yb);
		x[++topx]=e[i].xa;x[++topx]=e[i].xb;
		y[++topy]=e[i].ya;y[++topy]=e[i].yb;
		e[i].xb--;e[i].yb--;
		x[++topx]=e[i].xb;y[++topy]=e[i].yb;
	}
	sort(x+1,x+topx+1);sort(y+1,y+topy+1);
	for(int i=1;i<=topx;i++)if(x[i]!=x[i-1])mpx[x[i]]=++cntx;
	for(int i=1;i<=topy;i++)if(y[i]!=y[i-1])mpy[y[i]]=++cnty;
	cntx++;cnty++;
	for(int i=1;i<=n;i++)
	{
		e[i].xa=mpx[e[i].xa];
		e[i].xb=mpx[e[i].xb];
		e[i].ya=mpy[e[i].ya];
		e[i].yb=mpy[e[i].yb];
	}
	for(int i=n;i;i--){res=1;add(rt,1,1,cntx,cnty,1,e[i].xa,e[i].ya,e[i].xb,e[i].yb);}
	printf("%d\n",ans+1);
	return 0;
}

---

rp++