机器学习实战-Logistics回归

Logistics回归：实战，有两个特征X0,X1.100个样本，进行Logistics回归

1.导入数据

 def load_data_set():
     """
     加载数据集
     :return:返回两个数组，普通数组
         data_arr -- 原始数据的特征
         label_arr -- 原始数据的标签，也就是每条样本对应的类别
     """
     data_arr=[]
     label_arr=[]
     f=open('TestSet.txt','r')
     for line in f.readlines():
         line_arr=line.strip().split()
         #为了方便计算，我们将x0的值设为1.0，也就是在每一行的开头添加一个1.0，作为x0
         data_arr.append([1.0,np.float(line_arr[0]),np.float(line_arr[1])])
         label_arr.append(int(line_arr[2]))
     return data_arr,label_arr

2. Logistics回归梯度上升优化算法

 def sigmoid(x):
     return 1.0/(1+np.exp(-x))

 def grad_ascent(data_arr,class_labels):
     """
     梯度上升法，其实就是因为使用了极大似然估计，这个大家有必要去看推导，只看代码感觉不太够
     :param data_arr: 传入的就是一个普通的数组，当然你传入一个二维的ndarray也行
     :param class_labels: class_labels 是类别标签，它是一个 1*100 的行向量。
                     为了便于矩阵计算，需要将该行向量转换为列向量，做法是将原向量转置，再将它赋值给label_mat
     :return:
     """
     data_mat=np.mat(data_arr)
     #变成矩阵之后进行转置
     label_mat=np.mat(class_labels).transpose()
     #获得数据的样本量和特征维度数
     m,n=np.shape(data_mat)
     #学习率
     alpha=0.001
     #最大迭代次数
     max_cycles=500
     # 生成一个长度和特征数相同的矩阵，此处n为3 -> [[1],[1],[1]]
     # weights 代表回归系数， 此处的 ones((n,1)) 创建一个长度和特征数相同的矩阵，其中的数全部都是 1
     weights=np.ones((n,1))
     for k in range(max_cycles):
         h=sigmoid(data_mat*weights)
         error=label_mat-h
         weights=weights+alpha*data_mat.transpose()*error
     return weights

3. 画出决策边界，即画出数据集合Logistics回归最佳拟合直接的函数

 def plot_best_fit(weights):
     """
     可视化
     :param weights:
     :return:
     """
     import matplotlib.pyplot as plt
     data_mat, label_mat = load_data_set()
     data_arr = np.array(data_mat)
     n = np.shape(data_mat)[0]
     x_cord1 = []
     y_cord1 = []
     x_cord2 = []
     y_cord2 = []
     for i in range(n):
         if int(label_mat[i]) == 1:
             x_cord1.append(data_arr[i, 1])
             y_cord1.append(data_arr[i, 2])
         else:
             x_cord2.append(data_arr[i, 1])
             y_cord2.append(data_arr[i, 2])
     fig = plt.figure()
     ax = fig.add_subplot(111)
     ax.scatter(x_cord1, y_cord1, s=30, color='k', marker='^')
     ax.scatter(x_cord2, y_cord2, s=30, color='red', marker='s')
     x = np.arange(-3.0, 3.0, 0.1)
     y = (-weights[0] - weights[1] * x) / weights[2]
     """
     y的由来，卧槽，是不是没看懂？
     首先理论上是这个样子的。
     dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
     w0*x0+w1*x1+w2*x2=f(x)
     x0最开始就设置为1叻， x2就是我们画图的y值，而f(x)被我们磨合误差给算到w0,w1,w2身上去了
     所以： w0+w1*x+w2*y=0 => y = (-w0-w1*x)/w2
     """
     ax.plot(x, y)
     plt.xlabel('x1')
     plt.ylabel('y1')
     plt.show()

4. 测试数据，画图

 def test():
     """
     这个函数只要就是对上面的几个算法的测试，这样就不用每次都在power shell 里面操作，不然麻烦死了
     :return:
     """
     data_arr, class_labels = load_data_set()
     # 注意，这里的grad_ascent返回的是一个 matrix, 所以要使用getA方法变成ndarray类型
     weights = grad_ascent(data_arr, class_labels).getA()
     # weights = stoc_grad_ascent0(np.array(data_arr), class_labels)
     #weights = stoc_grad_ascent1(np.array(data_arr), class_labels)
     plot_best_fit(weights)

 if __name__ == '__main__':
     test()

5. 结果如下

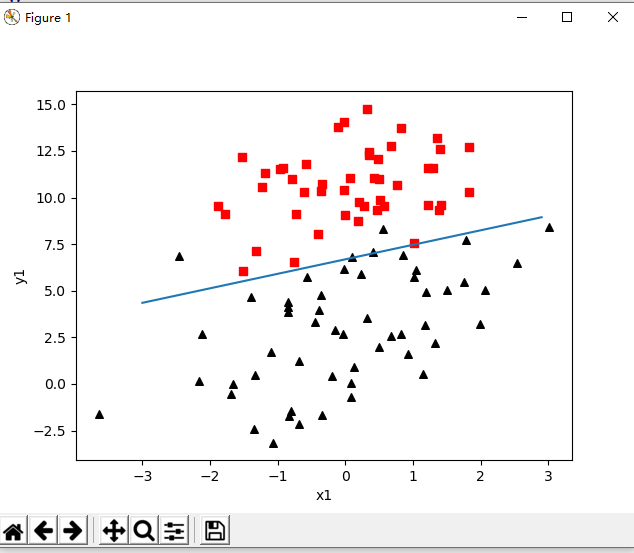
另外，还有

真实训练数据和测试数据-------从疝气病症预测病马的死亡率------
如何预测的代码也附加~
github实现地址：https://github.com/CynthiaWendy/Machine-Learning-in-Action-Logistics