【小知识】比较 x^y 和 y^x 的大小

往前翻几个编号相邻的题目翻到了这么一道题，感觉很好奇就做了一下

（upd：我下午问了下出题人做法，他就把题隐藏了……这不太友好啊……所以我补一下题意：）

题意

　　给你两个整数 $x$ 和 $y$，求 $x^y$ 和 $y^x$ 的大小关系。输出 $-1$ 表示前者大，$1$ 表示后者大，$0$ 表示一样大。

　　$0\le x\le 10^{3000}, -100\le y\le 10^{3000}$

题解

首先特判 $x$ 或 $y$ 为 $0$，$y=-1$ 以及 $y\lt -1$ 的情况。

对于剩下的正常情况，显然幂可以取对数转化为乘数。

即把 $x^y$ 取 $\ln$ 转化为 $y\ln{x}$，$y^x$ 取 $\ln$ 转化为 $x\ln{y}$

然后 $x^y$ 和 $y^x$ 的大小关系等于 $y\ln{x}$ 和 $x\ln{y}$ 的大小关系

移项，可得等于 $\frac{\ln{x}}{x}$ 和 $\frac{\ln{y}}{y}$ 的大小关系

咋一看，$\ln{x}$ 的变化速率显然比 $x$ 小很多啊！那我们是否可以大胆猜测，$x$ 越大，$\frac{\ln{x}}{x}$ 越小呢？

但我们没有给 $x$ 的定义域。

我们直觉上认为 $x$ 的定义域为 $[1,\infty)$ 的整数。

但我们没有证明这个结论，下面用实践来检验一下。

我们画一下 $y=\frac{\ln{x}}{x}$ 的图象

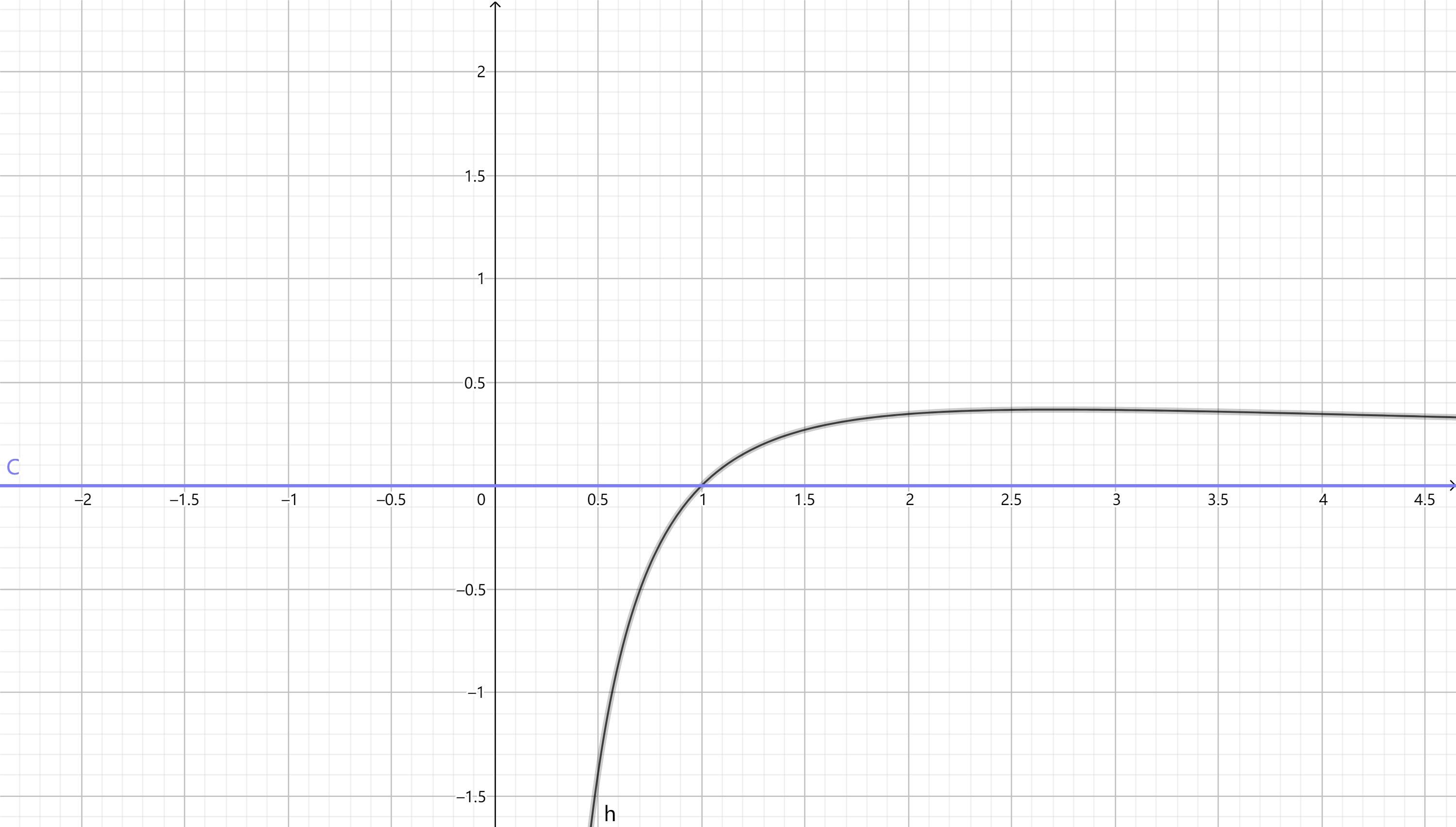
有没有观察到最高点的横坐标为 $e$？

那我们之前猜的那个结论好像就不对了

这是偶然吗？我们把 $log$ 的底数换成 $10$ 画一下看看

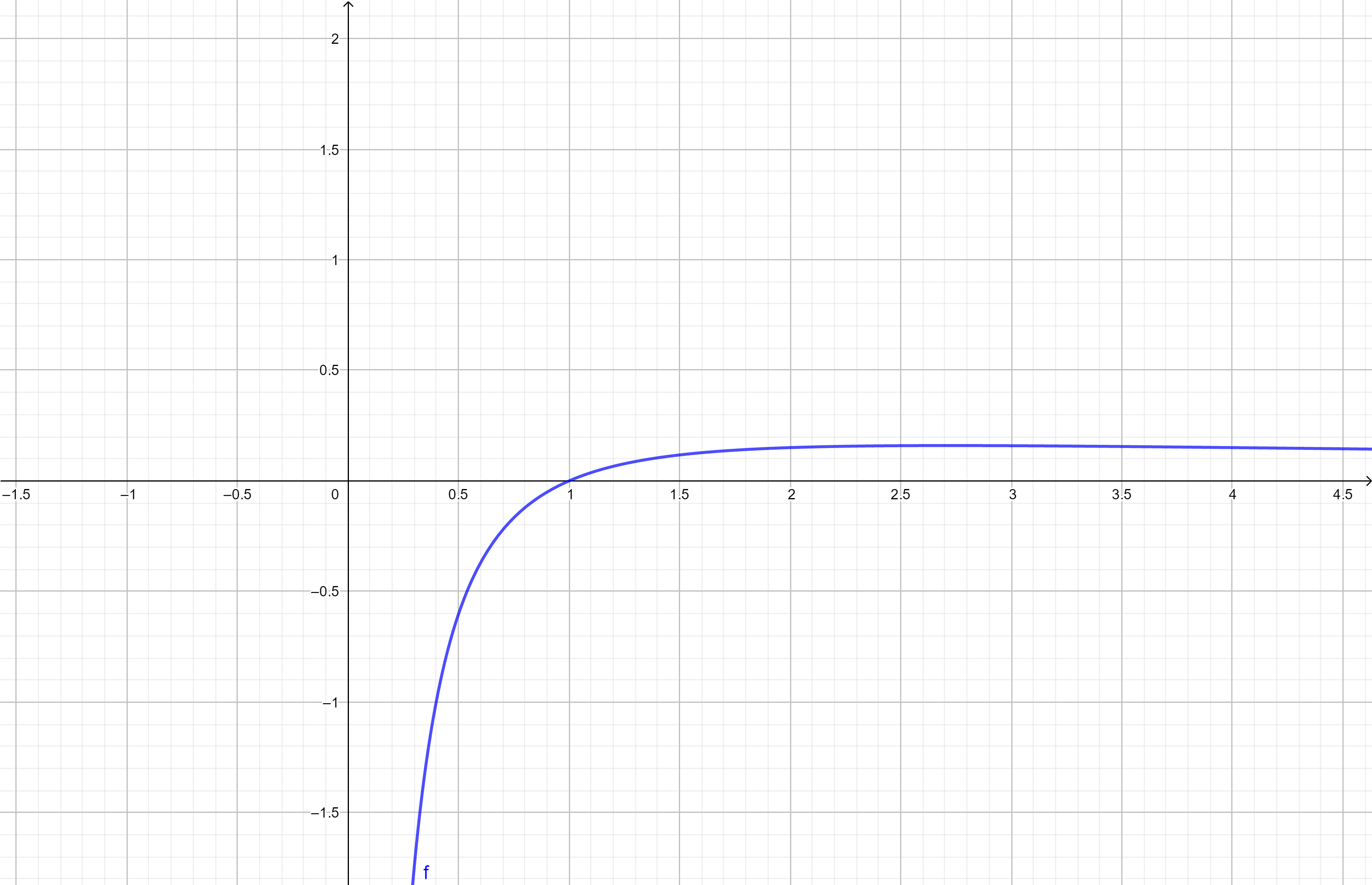
再把底数换成 $2$ 看看

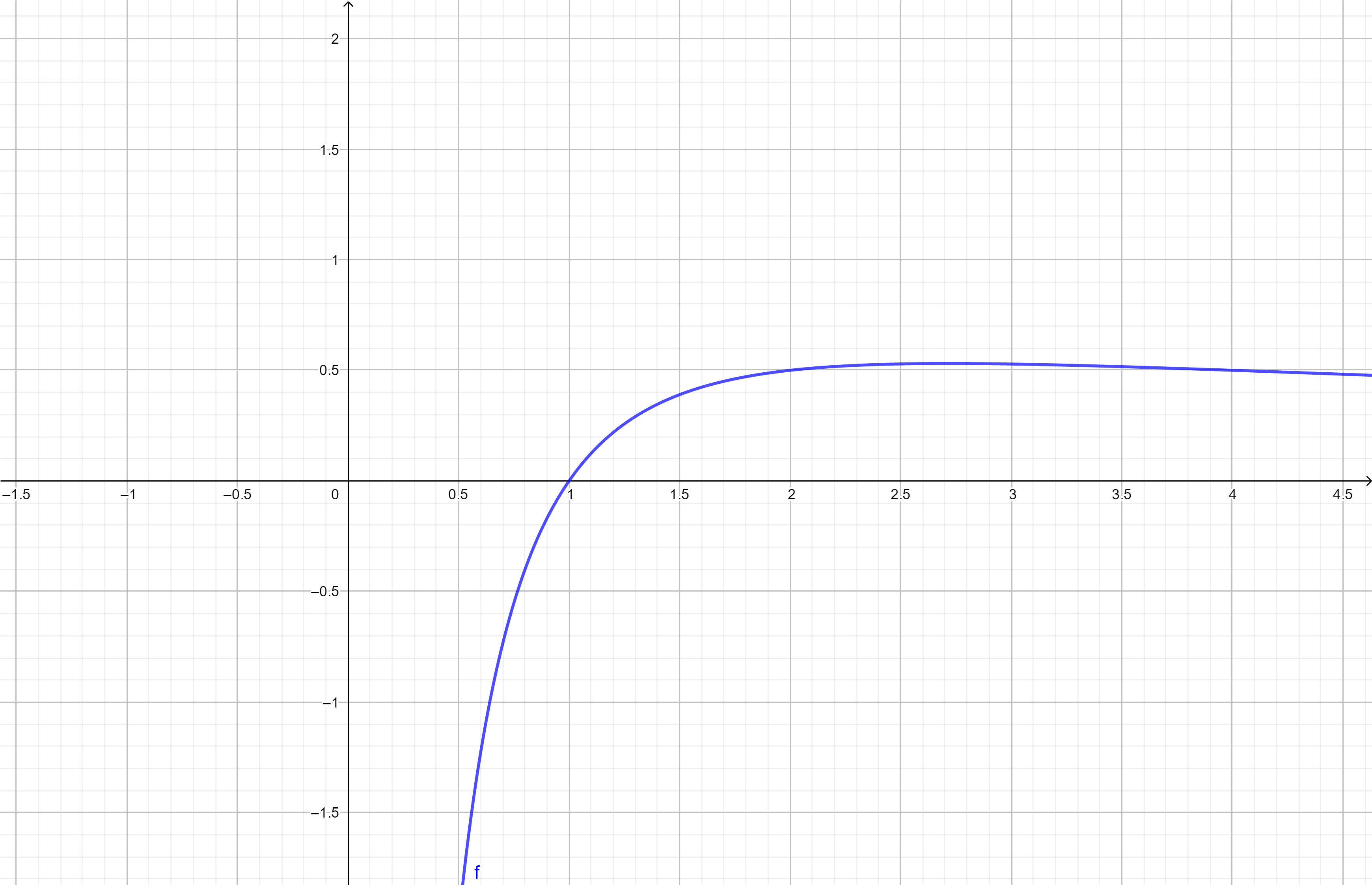
为什么无论底数是几，最高点的横坐标都是 $e$？

咱们来脑残证明一波：

首先，换底只会使图象沿 $y$ 轴成比例伸缩，不会改变最高点。因为假设把底数 $a$ 换成 $b$，那根据换底公式可得 $\log_b{x} = \log_a{x}\times \log_b{a}$，$\log_b{a}$ 是个与 $y$ 无关的常数，所以 $y=\frac{\log_a{x}}{x}$ 的图象只沿 $y$ 轴伸长 $\log_b{a}$ 倍，最高点横坐标不变。

但是这个结论是封闭的，即我们需要找到一个 $x$，使得 $y=\frac{\log_a{x}}{x}$ 的图象最高点能通过其它方式求出来。

当 $x=e$ 时就可以证明这个图象的最高点的横坐标是 $e$，证明方法：

考虑求导，分数的导数公式为 $(\frac{u}{v})' = \frac{u'v-uv'}{v^2}$

令 $u=\ln{x}$，$v=x$

$y=\ln{x}$ 的导数为 $y'=\frac{1}{x}$（至于这个核心公式怎么证，您们还是去查吧，这里篇幅不够且我能力有限），所以 $u'=\frac{1}{x}$，$v'=1$。

推得 $(\frac{\ln{x}}{x})' = \frac{1-\ln{x}}{x^2}$

因为该函数只有最大值，没有最小值，所以图象上导数为 $0$ 的点就是最高点。

于是最高点的横坐标就是 $\frac{1-\ln{x}}{x^2} = 0$ 的解，容易解得 $x=e$。

至此我们证明了当 $x=e$ 时就可以证明这个图象的最高点的横坐标是 $e$，根据前文可知换底不会改变图象最高点，故无论底数 $a$ 为多少，$y=\frac{\log_a{x}}{x}$ 的图象最高点的横坐标都是 $e$。

综上，函数在 $[1,e]$ 区间递增，$[e,\infty)$ 区间递减。

我们再求一下图象上与横坐标为 $2$ 的点的纵坐标相同的另一点，即求解 $2^x=x^2$。这个通过枚举就可以解得 $x=4$。所以图象在 $x=2$ 与 $x=4$ 处的纵坐标相同。

有了函数的分段变化情况，我们就可以判断 $\frac{\ln{x}}{x}$ 和 $\frac{\ln{y}}{y}$ 的大小关系了。

大力分类讨论即可。