java8学习之groupingByConcurrent与partioningBy源码分析

在上一次【http://www.cnblogs.com/webor2006/p/8387656.html】中对于Collectors.groupingBy()方法进行了完整的分析之后，接着继续来分析一下Collectors其它跟它类似的方法：groupingByConcurrent()、partioningBy()，

groupingByConcurrent():

这个方法在分析最复杂的groupingBy()时在其javadoc上提到过，如下：

而跟groupingBy()方法类似，Collectors也提供了三个重载的方法，如下：

所以分析也是从简到难顺序进行，首先先看一下最简单的：

首先先简单读一下它的javadoc：

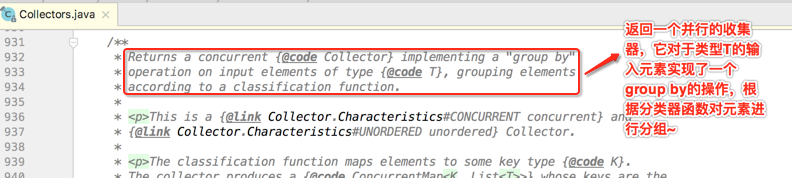
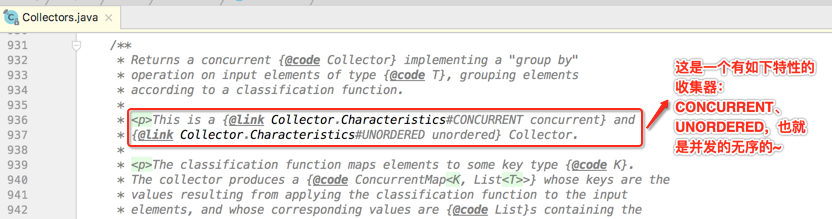
接着看一下它的具体实现：

接着它调用了另外一个重载的方法，跟groupingBy类似，最终会调用一个最复杂的，如下：

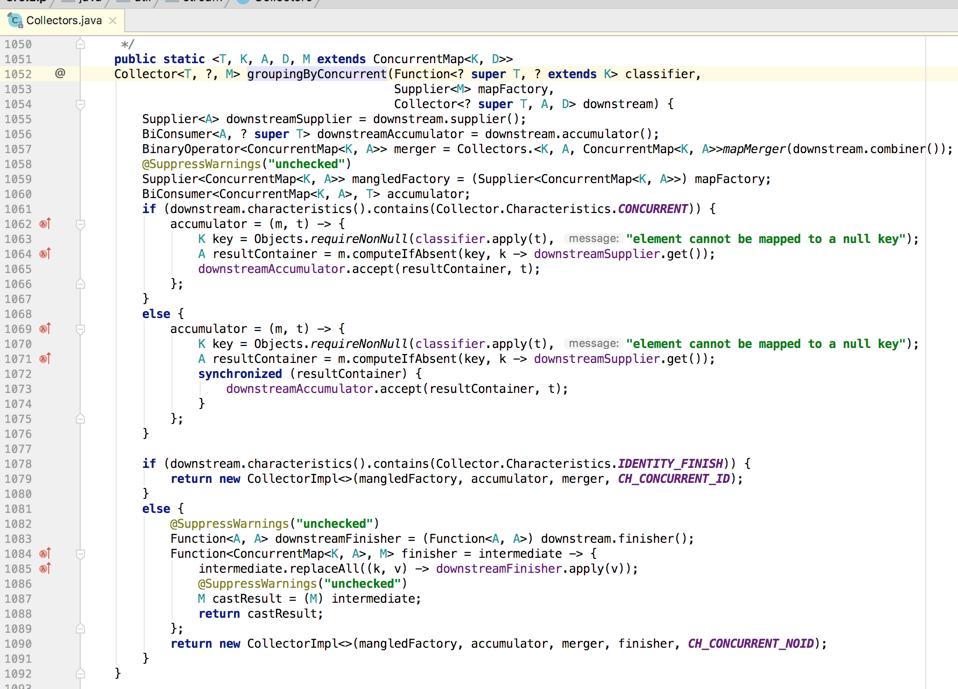
其代码的实现跟groupingBy基本雷同，相同的部份这里就不多说了，只看不同的：

这就意味着对于不包含CONCURRENT的流如果调用groupingByConcurrent()方法也不会出错，因为从实现中也发现它会对结果容器进行同步处理；而反过来，如果对于一个并行流来说也没有提供CONCURRENT特性，此时多个线程就对应多个中间结果容器，这时也是对结果进行累加，也没啥问题。

partioningBy():

跟分组相关的方法那就是分区啦，同样存在重载的方式，如下：

还是按易到难的顺序进行分析，先分析它：

而它的实现是调用了另外一个重载的partitioningBy()方法：

所以焦点转向这个复杂的partitioningBy()方法：

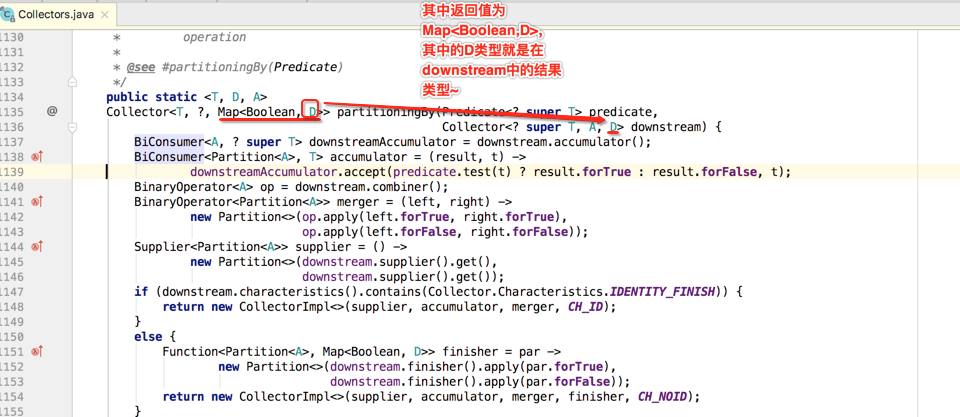
接着再看一下方法的具体实现，其大体过程跟咱们之前分析的groupingBy()方法基本类似，下面开始：

然后再依据下游的这个累加器生成新的累加器，具体细节如下：

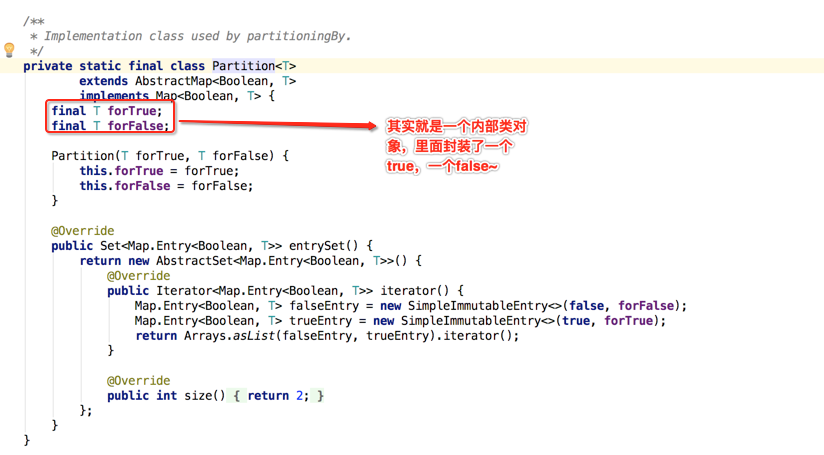
那为啥有了Map结构还得自己封装一个这样的内部类呢？很明显就是为了应用于咱们这个只有两组的特殊情况而生的嘛。

接着再根据下游收集器的combiner()对象再生成一个新的合并对象，如下：

最后再根据下游收集器supplier再生成一个新的supplier,如下：

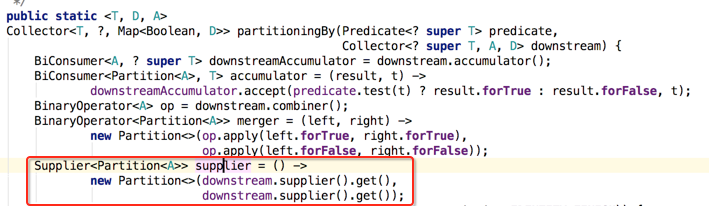
接下来则就是实例化CollectorImpl对象，当然也是根据下游收集器的特性来进行的，如下：

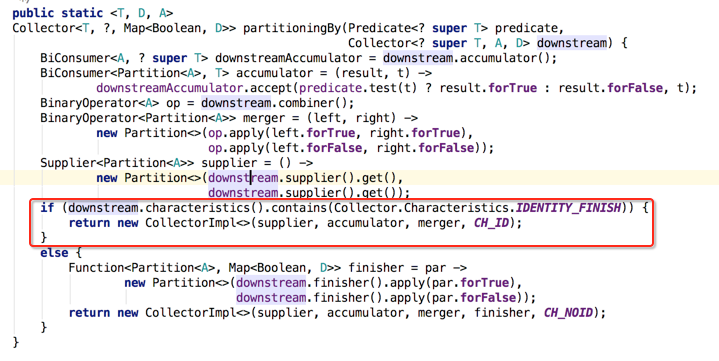
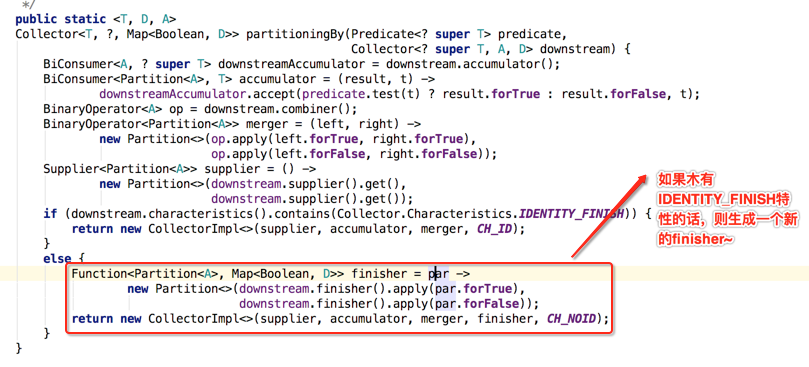
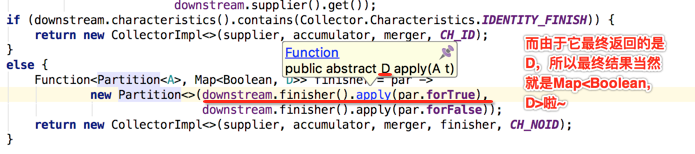
至此，partitioningBy()方法就已经分析完啦，当然Collectors中的所有方法的实现基本上都已经完全读完了，通过读这些源码发现对于之前在学习之初学习的各种函数式接口、Lambda表达式的这些基础知识是何等的重要，基本上每个方法的实现都脱离不开这些基础知识，另外能过源码的认识也让咱们学得更加扎实。