两种非常常见的非线性单元：rectified linear units (ReLUs) 和 leaky ReLUs

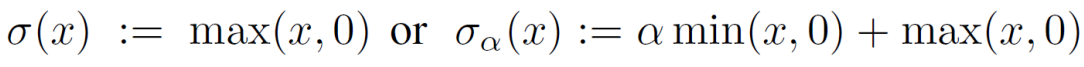
我们选取binary hinge loss进行二分类

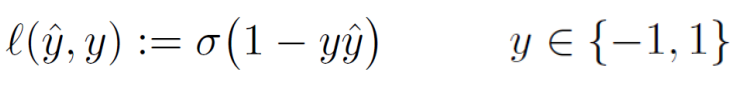
对于多分类，我们可以定义multiclass hinge loss

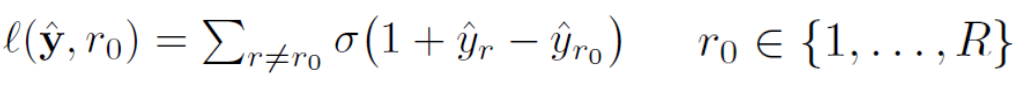
定义Ω为网络的参数空间， L(ω)为loss。

由于我们选了ReLU非线性单元作为loss, 那么L(ω)是分片线性的。对于参数空间，我们可以将其进行一个划分，

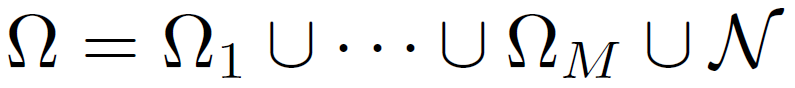
分成有限个open cells Ωu 和 边界N，则损失函数L(ω)在cell的内部是光滑的，在边界上是不可微的。

下面我们将loss限制在某个cell  Ωu上单独考虑，并且loss拥有multilinear form. 由于multilinear form是调和的，由strong maximum principle知，极值点必定在边界处N. 换句话说，ReLU 神经网络 with hinge loss L(ω)是不存在可微的局部极值点的。

目前为止，我们可以知道局部极值有两种情况，

Type I (Flat). 局部极值在cell中，loss为常值。

Type II (Sharp). 局部极值在边界N上。

Main Result 1.   在Type II局部极值点，L(ω)>0.

也就是说，如果存在极值0，那么Type II极值点都是sub-optimal的。

若我们考虑更一般的情况：fully connected networks with leaky ReLU nonlinearities. 那么我们有以下结果，

Main Result 2.  在Type I局部极值点，L(ω)=0. 在Type II局部极值点，L(ω)>0.

在存在极值0的情况下，flat 局部极小值都是optimal的，sharp 局部极小值都是sub-optimal的。若不存在极值0，所有的局部极值点都是sharp的。

未完待续。。。

The Multilinear Structure of ReLU Networks的更多相关文章

  1. 课程一(Neural Networks and Deep Learning)，第四周（Deep Neural Networks） —— 3.Programming Assignments: Deep Neural Network - Application

    Deep Neural Network - Application Congratulations! Welcome to the fourth programming exercise of the ...

  2. DEEP LEARNING WITH STRUCTURE

    DEEP LEARNING WITH STRUCTURE Charlie Tang is a PhD student in the Machine Learning group at the Univ ...

  3. 课程一(Neural Networks and Deep Learning)总结——2、Deep Neural Networks

    Deep L-layer neural network 1 - General methodology As usual you will follow the Deep Learning metho ...

  4. 深度学习材料：从感知机到深度网络A Deep Learning Tutorial: From Perceptrons to Deep Networks

    In recent years, there’s been a resurgence in the field of Artificial Intelligence. It’s spread beyo ...

  5. [综述]Deep Compression/Acceleration深度压缩/加速/量化

    Survey Recent Advances in Efficient Computation of Deep Convolutional Neural Networks, [arxiv '18] A ...

  6. 网络压缩论文集(network compression)

    Convolutional Neural Networks ImageNet Models Architecture Design Activation Functions Visualization ...

  7. CVPR 2017 Paper list

    CVPR2017 paper list Machine Learning 1 Spotlight 1-1A Exclusivity-Consistency Regularized Multi-View ...

  8. (转) Deep Reinforcement Learning: Playing a Racing Game

    Byte Tank Posts Archive Deep Reinforcement Learning: Playing a Racing Game OCT 6TH, 2016 Agent playi ...

  9. 社区发现算法问题&&NetworkX&&Gephi

    在做东西的时候用到了社区发现,因此了解了一下有关社区发现的一些问题 1,社区发现算法 (1)SCAN:一种基于密度的社团发现算法 Paper: <SCAN: A Structural Clust ...

随机推荐

  1. Ubunut16.04 安装 Mahout

    近期笔者想安装mahout,看到网上教程过于陈旧,故记录之 转载请包含 http://www.cnblogs.com/lqruui/p/6037680.html 1.下载mahout   mahout ...

  2. Python内置函数reversed()用法分析

    Python内置函数reversed()用法分析 这篇文章主要介绍了Python内置函数reversed()用法,结合实例形式分析了reversed()函数的功能及针对序列元素相关操作技巧与使用注意事 ...

  3. 有关face的好文MARK集

    Single Stage Headless Face Detector 据说已经超过了tiny face DDFD <Multi-view Face Detection Using Deep C ...

  4. idea Ctrl+Alt+T 快捷键失效

    idea快捷键 CTRL+ALT+T  把选中的代码放在 TRY{} IF{} ELSE{} 里 这个快捷键失效了,显然是热键冲突,查看了喜欢占热键的输入法.词典.微信.qq.都没找到占用,最后发现 ...

  5. Python爬虫学习==>第六章：爬虫的基本原理

    学习目的: 掌握爬虫相关的基本概念 正式步骤 Step1:什么是爬虫 请求网站并提取数据的自动化程序 Step2:爬虫的基本流程 Step3:Request和Response 1.request 2. ...

  6. 导模块的细节：（跨文件导入模块 &模块的两种执行方式） | 包的概念与使用 | 包中的相对导入语法

    今日内容 包: 1. 导入模块的细节 2. 包的概念与使用 3. 包中的相对导入语法 跨文件夹导入模块 1. 假设有一个文件夹a ,a 的下面有一个ma 的模块,如果a文件夹所在目录在环境变量,a文件 ...

  7. 使用URLOS在linux系统中极速部署NFS共享存储服务

    如何在linux系统里搭建NFS服务?其实我们只需要安装一个URLOS面板,然后就能在3分钟内将NFS服务部署完成.近日,URLOS在应用市场中上架了一款NFS应用,它可以让我们的节点主机在3分钟内极 ...

  8. 【神经网络与深度学习】卷积神经网络（CNN）

    [神经网络与深度学习]卷积神经网络(CNN) 标签:[神经网络与深度学习] 实际上前面已经发布过一次,但是这次重新复习了一下,决定再发博一次. 说明:以后的总结,还应该以我的认识进行总结,这样比较符合 ...

  9. mysql的root密码忘了

    忘记密码:https://www.cnblogs.com/ryanzheng/p/9348723.htmlmy.cnf的[mysqld]下加:skip-grant-tables重启 mysql -ur ...

  10. 21天学通Python课后实验题4.6

    21天学通Python课后实验题4.6 1. 编程实现用户输入一门课程的两门子课程成绩,第一门子课程60分以上,则显示“通过”,第一门子课程不及格,则显示“未通过”,第一门子课程及格,而第二门子课程不 ...