[BZOJ2822]:[AHOI2012]树屋阶梯（卡特兰数）

题目传送门

---

题目描述

暑假期间，小龙报名了一个模拟野外生存作战训练班来锻炼体魄，训练的第一个晚上，教官就给他们出了个难题。由于地上露营湿气重，必须选择在高处的树屋露营。小龙分配的树屋建立在一颗高度为N+1尺（N为正整数）的大树上，正当他发愁怎么爬上去的时候，发现旁边堆满了一些空心四方钢材（如图），经过观察和测量，这些钢材截面的宽和高大小不一，但都是1尺的整数倍，教官命令队员们每人选取N个空心钢材来搭建一个总高度为N尺的阶梯来进入树屋，该阶梯每一步台阶的高度为1尺，宽度也为1尺。如果这些钢材有各种尺寸，且每种尺寸数量充足，那么小龙可以有多少种搭建方法？（注：为了避免夜里踏空，钢材空心的一面绝对不可以向上。）

---

输入格式

一个正整数N，表示阶梯的高度。

---

输出格式

一个正整数，表示搭建方法的个数。（注：搭建方法个数可能很大。）

---

样例

样例输入

3

样例输出

5

---

数据范围与提示

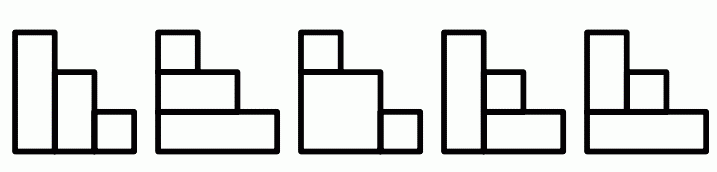
样例说明：

数据范围：

对于全部数据，$N \leqslant 100$。

---

题解

根据个人做题经验，看到样例输入3，样例输出5，优先考虑卡特兰数。

根据数据范围，可以使用分解质因数和高精度两种做法求出卡特兰数。

---

代码时刻

分解质因数+高精乘低精：

#include<bits/stdc++.h>
using namespace std;
int n;
int pre[2000001],pri[2000001];
int wzc[2000001];
int l=1;
long long ans[100001],flag1,flag2;
void pre_work()
{
	ans[1]=1;
	for(int i=2;i<=2*n;i++)
	{
		if(!pri[i])
		{
			pri[i]=i;
			pre[++pre[0]]=i;
		}
		for(int j=1;j<=pre[0];j++)
		{
			if(pre[j]>pri[i]||i*pre[j]>2*n)break;
			pri[i*pre[j]]=pre[j];
		}
	}
}
void mul(int x)
{
    flag2=0;
    for(int i=1;i<=l;i++)
    {
        flag1=ans[i]*x;
        ans[i]=flag1%1000000000000000+flag2;
        flag2=flag1/1000000000000000;
    }
    if(flag2)ans[++l]=flag2;
}
int main()
{
	scanf("%d",&n);
	pre_work();
	for(int i=n+2;i<=2*n;i++)
	{
		int flag=i;
		while(flag>1)
		{
			wzc[pri[flag]]++;
			flag/=pri[flag];
		}
	}
	for(int i=2;i<=n;i++)
	{
		int flag=i;
		while(flag>1)
		{
			wzc[pri[flag]]--;
			flag/=pri[flag];
		}
	}
	for(int i=1;i<=2*n;i++)
		for(int j=1;j<=wzc[i];j++)
			mul(i);
	printf("%lld",ans[l]);
    while(--l)printf("%.15lld",ans[l]);
	return 0;
}

高精度：

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a[100000],c[100000];
int mu[5001];
void mul(register int p)
{
	register int x=0,j;
	for(j=1;j<=a[0];j++)
	{
		a[j]=a[j]*p+x;
		x=a[j]/10;
		a[j]%=10;
	}
	a[j]=x;
	while(a[j]>9)
	{
		a[j+1]=a[j]/10;
		a[j]%=10;
		j++;
	}
	while(a[j]==0&&j>1)j--;
	a[0]=j;
}
void chu(register int b)
{
    register int x=0,s=0,t=0;
    memset(c,0,sizeof(c));
    for(register int i=1;i<=a[0];i++)
    {
        x=x*10+a[i];
        if(x/b!=0)s++;
        if(s==0)continue;
        c[++t]=x/b;
        x%=b;
    }
    for(register int i=1;i<=t;i++)
    	a[i]=c[i];
    a[0]=t;
}
int main()
{
	a[0]=a[1]=1;
	scanf("%d",&n);
	for(register int i=n+2;i<=2*n;i++)mul(i);
	reverse(a+1,a+a[0]+1);
	for(register int i=2;i<=n;i++)chu(i);
	for(register int i=1;i<=a[0];i++)printf("%d",a[i]);
}

---

rp++