关于交叉熵（cross entropy），你了解哪些

二分~多分~Softmax~理预

一、简介

　在二分类问题中，你可以根据神经网络节点的输出，通过一个激活函数如Sigmoid，将其转换为属于某一类的概率，为了给出具体的分类结果，你可以取0.5作为阈值，凡是大于0.5的样本被认为是正类，小于0.5则认为是负类

　然而这样的做法并不容易推广到多分类问题。多分类问题神经网络最常用的方法是根据类别个数n，设置n个输出节点，这样每个样本神经网络都会给出一个n维数组作为输出结果，然后我们运用激活函数如softmax，将输出转换为一种概率分布，其中的每一个概率代表了该样本属于某类的概率。

　比如一个手写数字识别这种简单的10分类问题，对于数字1的识别，神经网络模型的输出结果应该越接近\([0, 1, 0, 0, 0, 0, 0, 0, 0, 0]\)越好，其中\([0, 1, 0, 0, 0, 0, 0, 0, 0, 0]\)是最理想的结果了

　但是如何衡量一个神经网络输出向量和理想的向量的接近程度呢？交叉熵（cross entropy）就是这个评价方法之一，他刻画了两个概率分布之间的距离，是多分类问题中常用的一种损失函数

二、交叉熵

　给定两个概率分布：p（理想结果即正确标签向量）和q（神经网络输出结果即经过softmax转换后的结果向量），则通过q来表示p的交叉熵为：

\(H(p, q) = - \sum_xp(x)logq(x)\)

　注意：既然p和q都是一种概率分布，那么对于任意的x，应该属于\([0, 1]\)并且所有概率和为1

\(\forall x p(X=x) \epsilon [0,1]\)且\(\sum_xp(X=x) =1\)

　交叉熵刻画的是通过概率分布q来表达概率分布p的困难程度，其中p是正确答案，q是预测值，也就是交叉熵值越小，两个概率分布越接近

三、三分类实例讲解交叉熵

　其中某个样本的正确答案即p是\([1,0, 0]\)，某模型经过Softmax激活后的答案即预测值q是\([0.5, 0.4, 0.1]\)，那么这个预测值和正确答案之间的交叉熵为：

\(H(p=[1,0,0], q=[0.5,0.4,0.1]) = -(1*log0.5 + 0*log0.4 + 0*log0.1) \approx 0.3\)

　如果另外一个模型的预测值q是\([0.8, 0.1, 0.1]\)，那么这个预测值和正确答案之间的交叉熵为：

\(H(p=[1,0,0], q=[0.8,0.1,0.1]) = -(1*log0.8 + 0*log0.1 + 0*log0.1) \approx 0.1\)

　从直观上可以很容易的知道第二个预测答案要优于第一个，通过交叉熵计算得到的结果也是一致的（第二个交叉熵值更小）

　而TF中很容易做到交叉熵的计算：

import tensorflow as tf

cross_entropy = -tf.reduce_mean( y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)) )

　上述代码包含了四种不同的TF运算，解释如下：

　1）tf.clip_by_value()：将一个张量中的数值限制在一个范围内，如限制在\([0.1, 1.0]\)范围内，可以避免一些运算错误，如预测结果q中元素可能为0，这样的话log0是无效的

v = tf.constant([[1.0, 2.0, 3.0], [4.0,5.0,6.0] ])
with tf.Session() as sess:
	sess.run(tf.global_variables_initializer())
	print(tf.clip_by_value(v, 2.5, 4.5).eval())

　　

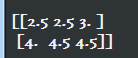
　2）tf.log()：对张量中的所有元素依次求对数

v = tf.constant([[1.0, 2.0, 3.0], [4.0,5.0,6.0] ])
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print(tf.log(v).eval())

　　

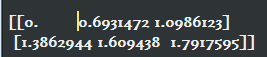
　3）乘法运算：*操作，是元素之间直接相乘，而矩阵相乘用tf.matmul函数来完成

v1 = tf.constant([ [1.0, 2.0], [3.0, 4.0]])
v2 = tf.constant([ [5.0, 6.0], [7.0, 8.0]])
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print( (v1 * v2).eval() )
    print( tf.matmul(v1, v2).eval() )

　　

　4）求和：上面三个运算完成了每个样例中每个类别的交叉熵\(p(x)logq(x)\)的计算，还未进行求和运算

　　即：三步计算后得到的结果是个n * m的二维矩阵，其中n为一个batch中样本数量，m为分类的类别数量，比如十分类问题，m为10.根据交叉熵公式

　　最后是要将每行中m个结果相加得到每个样本的交叉熵，然后再对这n行取平均得到一个batch的平均交叉熵，即-tf.reduce_mean()函数来实现

　总结：因为交叉熵一般会与softmax一起使用，所以TF对这两个功能进行了封装，并提供了tf.nn.softmax_cross_entropy_with_logits函数

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, y_)
#y:原始神经网络的输出结果
#y_:标准答案
#这样一个函数即可实现使用了Softmax后的交叉熵

　关于Softmax计算过程，可以参考：实战Google深度学习框架-C4-深层神经网络