参考：https://blog.csdn.net/u013733326/article/details/79767169

希望大家直接到上面的网址去查看代码，下面是本人的笔记

两层神经网络，和吴恩达课后作业学习1-week3-homework-one-hidden-layer——不发布不同之处在于使用的函数不同线性->ReLU->线性->sigmod函数，训练的数据也不同，这里训练的是之前吴恩达课后作业学习1-week2-homework-logistic中的数据，判断是否为猫，查看使用两层的效果是否比一层好

1.准备软件包

  1. import numpy as np
  2. import h5py
  3. import matplotlib.pyplot as plt
  4. import testCases #参见资料包，或者在文章底部copy
  5. from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward #参见资料包
  6. import lr_utils #参见资料包，或者在文章底部copy

为了和作者的数据匹配，需要指定随机种子

  1. np.random.seed()

2.初始化参数

模型结构是线性->ReLU->线性->sigmod函数

  1. def initialize_parameters(n_x,n_h,n_y):
  2.     """
  3.     此函数是为了初始化两层网络参数而使用的函数。
  4.     参数：
  5.         n_x - 输入层节点数量
  6.         n_h - 隐藏层节点数量
  7.         n_y - 输出层节点数量
  8.  
  9.     返回：
  10.         parameters - 包含你的参数的python字典：
  11.             W1 - 权重矩阵,维度为（n_h，n_x）
  12.             b1 - 偏向量，维度为（n_h，）
  13.             W2 - 权重矩阵，维度为（n_y，n_h）
  14.             b2 - 偏向量，维度为（n_y，）
  15.  
  16.     """
  17.     W1 = np.random.randn(n_h, n_x) * 0.01 #随机初始化参数
  18.     b1 = np.zeros((n_h, ))
  19.     W2 = np.random.randn(n_y, n_h) * 0.01
  20.     b2 = np.zeros((n_y, ))
  21.  
  22.     #使用断言确保我的数据格式是正确的
  23.     assert(W1.shape == (n_h, n_x))
  24.     assert(b1.shape == (n_h, ))
  25.     assert(W2.shape == (n_y, n_h))
  26.     assert(b2.shape == (n_y, ))
  27.  
  28.     parameters = {"W1": W1,
  29.                   "b1": b1,
  30.                   "W2": W2,
  31.                   "b2": b2}
  32.  
  33.     return parameters

测试：

  1. print("==============测试initialize_parameters==============")
  2. parameters = initialize_parameters(,,)
  3. print("W1 = " + str(parameters["W1"]))
  4. print("b1 = " + str(parameters["b1"]))
  5. print("W2 = " + str(parameters["W2"]))
  6. print("b2 = " + str(parameters["b2"]))

返回：

  1. ==============测试initialize_parameters==============
  2. W1 = [[ 0.01624345 -0.00611756 -0.00528172]
  3.  [-0.01072969  0.00865408 -0.02301539]]
  4. b1 = [[.]
  5.  [.]]
  6. W2 = [[ 0.01744812 -0.00761207]]
  7. b2 = [[.]]

3.前向传播

1）线性部分

  1. def linear_forward(A,W,b):
  2.     """
  3.     实现前向传播的线性部分。
  4.  
  5.     参数：
  6.         A - 来自上一层（或输入数据）的激活，维度为(上一层的节点数量，示例的数量）
  7.         W - 权重矩阵，numpy数组，维度为（当前图层的节点数量，前一图层的节点数量）
  8.         b - 偏向量，numpy向量，维度为（当前图层节点数量，）
  9.  
  10.     返回：
  11.          Z - 激活功能的输入，也称为预激活参数
  12.          cache - 一个包含“A”，“W”和“b”的字典，存储这些变量以有效地计算后向传递
  13.     """
  14.     Z = np.dot(W,A) + b
  15.     assert(Z.shape == (W.shape[],A.shape[]))
  16.     cache = (A,W,b)
  17.  
  18.     return Z,cache

测试函数linear_forward_test_case()：

  1. def linear_forward_test_case(): #随机生成A,W,b,只有一层
  2.     np.random.seed()
  3.     """
  4.     X = np.array([[-1.02387576, 1.12397796],
  5.  [-1.62328545, 0.64667545],
  6.  [-1.74314104, -0.59664964]])
  7.     W = np.array([[ 0.74505627, 1.97611078, -1.24412333]])
  8.     b = np.array([[]])
  9.     """
  10.     A = np.random.randn(,)
  11.     W = np.random.randn(,)
  12.     b = np.random.randn(,)
  13.  
  14.     return A, W, b

测试：

  1. #测试linear_forward
  2. print("==============测试linear_forward==============")
  3. A,W,b = testCases.linear_forward_test_case()
  4. Z,linear_cache = linear_forward(A,W,b)
  5. print("Z = " + str(Z))
    print(linear_cache

返回：

  1. ==============测试linear_forward==============
  2. Z = [[ 3.26295337 -1.23429987]]
  3. (array([[ 1.62434536, -0.61175641],
  4.        [-0.52817175, -1.07296862],
  5.        [ 0.86540763, -2.3015387 ]]), array([[ 1.74481176, -0.7612069 ,  0.3190391 ]]), array([[-0.24937038]]))

2）线性激活部分

  1. def linear_activation_forward(A_prev,W,b,activation): #activation为指定使用的激活函数
  2.     """
  3.     实现LINEAR-> ACTIVATION 这一层的前向传播
  4.  
  5.     参数：
  6.         A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数）
  7.         W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
  8.         b - 偏向量，numpy阵列，维度为（当前层的节点数量，）
  9.         activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
  10.  
  11.     返回：
  12.         A - 激活函数的输出，也称为激活后的值
  13.         cache - 一个包含“linear_cache”和“activation_cache”的字典，我们需要存储它以有效地计算后向传递
  14.     """
  15.  
  16.     if activation == "sigmoid":
  17.         Z, linear_cache = linear_forward(A_prev, W, b)
  18.         A, activation_cache = sigmoid(Z)
  19.     elif activation == "relu":
  20.         Z, linear_cache = linear_forward(A_prev, W, b)
  21.         A, activation_cache = relu(Z)
  22.  
  23.     assert(A.shape == (W.shape[],A_prev.shape[]))
  24.     cache = (linear_cache,activation_cache)
  25.  
  26.     return A,cache

测试函数为：

  1. def linear_activation_forward_test_case(): #单层
  2.     """
  3.     X = np.array([[-1.02387576, 1.12397796],
  4.  [-1.62328545, 0.64667545],
  5.  [-1.74314104, -0.59664964]])
  6.     W = np.array([[ 0.74505627, 1.97611078, -1.24412333]])
  7.     b =
  8.     """
  9.     np.random.seed()
  10.     A_prev = np.random.randn(,)
  11.     W = np.random.randn(,)
  12.     b = np.random.randn(,)
  13.     return A_prev, W, b

测试：

  1. #测试linear_activation_forward
  2. print("==============测试linear_activation_forward==============")
  3. A_prev, W,b = testCases.linear_activation_forward_test_case()
  4.  
  5. #使用sigmoid激活函数
  6. A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
  7. print("sigmoid，A = " + str(A))
  8. print(linear_activation_cache)
  9.  
  10. #使用relu激活函数
  11. A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
  12. print("ReLU，A = " + str(A))
  13. print(linear_activation_cache)

返回：

  1. ==============测试linear_activation_forward==============
  2. sigmoid，A = [[0.96890023 0.11013289]]
  3. ((array([[-0.41675785, -0.05626683],
  4.        [-2.1361961 ,  1.64027081],
  5.        [-1.79343559, -0.84174737]]), array([[ 0.50288142, -1.24528809, -1.05795222]]), array([[-0.90900761]])), array([[ 3.43896131, -2.08938436]]))
  6. ReLU，A = [[3.43896131 .        ]]
  7. ((array([[-0.41675785, -0.05626683],
  8.        [-2.1361961 ,  1.64027081],
  9.        [-1.79343559, -0.84174737]]), array([[ 0.50288142, -1.24528809, -1.05795222]]), array([[-0.90900761]])), array([[ 3.43896131, -2.08938436]]))

4.计算成本

  1. def compute_cost(AL,Y):
  2.     """
  3.     实施等式（）定义的成本函数。
  4.  
  5.     参数：
  6.         AL - 与标签预测相对应的概率向量，维度为（，示例数量）
  7.         Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（，数量）
  8.  
  9.     返回：
  10.         cost - 交叉熵成本
  11.     """
  12.     m = Y.shape[]
  13.     cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log( - AL),  - Y)) / m
  14.  
  15.     cost = np.squeeze(cost)
  16.     assert(cost.shape == ())
  17.  
  18.     return cost

测试函数：

  1. def compute_cost_test_case():
  2.     Y = np.asarray([[, , ]])
  3.     aL = np.array([[.,.,0.4]])
  4.  
  5.     return Y, aL

测试：

  1. #测试compute_cost
  2. print("==============测试compute_cost==============")
  3. Y,AL = testCases.compute_cost_test_case()
  4. print("cost = " + str(compute_cost(AL, Y)))

返回：

  1. ==============测试compute_cost==============
  2. cost = 0.414931599615397

5.反向传播

其实是先通过线性激活部分后向传播得到dz，然后再将dz带入线性部分的后向传播得到dw,db,dA_prev

1）线性部分

根据这三个公式来构建后向传播函数

  1. def linear_backward(dZ,cache):
  2.     """
  3.     为单层实现反向传播的线性部分（第L层）
  4.  
  5.     参数：
  6.          dZ - 相对于（当前第l层的）线性输出的成本梯度
  7.          cache - 来自当前层前向传播的值的元组（A_prev，W，b）
  8.  
  9.     返回：
  10.          dA_prev - 相对于激活（前一层l-）的成本梯度，与A_prev维度相同
  11.          dW - 相对于W（当前层l）的成本梯度，与W的维度相同
  12.          db - 相对于b（当前层l）的成本梯度，与b维度相同
  13.     """
  14.     A_prev, W, b = cache
  15.     m = A_prev.shape[]
  16.     dW = np.dot(dZ, A_prev.T) / m
  17.     db = np.sum(dZ, axis=, keepdims=True) / m
  18.     dA_prev = np.dot(W.T, dZ)
  19.  
  20.     assert (dA_prev.shape == A_prev.shape)
  21.     assert (dW.shape == W.shape)
  22.     assert (db.shape == b.shape)
  23.  
  24.     return dA_prev, dW, db

测试函数：

  1. def linear_backward_test_case(): #随机生成前向传播结果用于测试后向
  2.     """
  3.     z, linear_cache = (np.array([[-0.8019545 ,  3.85763489]]), (np.array([[-1.02387576,  1.12397796],
  4.        [-1.62328545,  0.64667545],
  5.        [-1.74314104, -0.59664964]]), np.array([[ 0.74505627,  1.97611078, -1.24412333]]), np.array([[]]))
  6.     """
  7.     np.random.seed()
  8.     dZ = np.random.randn(,)
  9.     A = np.random.randn(,)
  10.     W = np.random.randn(,)
  11.     b = np.random.randn(,)
  12.     linear_cache = (A, W, b)
  13.     return dZ, linear_cache

测试：

  1. #测试linear_backward
  2. print("==============测试linear_backward==============")
  3. dZ, linear_cache = testCases.linear_backward_test_case()
  4.  
  5. dA_prev, dW, db = linear_backward(dZ, linear_cache)
  6. print ("dA_prev = "+ str(dA_prev))
  7. print ("dW = " + str(dW))
  8. print ("db = " + str(db))

返回：

  1. ==============测试linear_backward==============
  2. dA_prev = [[ 0.51822968 -0.19517421]
  3.  [-0.40506361  0.15255393]
  4.  [ 2.37496825 -0.89445391]]
  5. dW = [[-0.10076895  1.40685096  1.64992505]]
  6. db = [[0.50629448]]

2）线性激活部分

将线性部分也使用了进来

在dnn_utils.py中定义了两个现成可用的后向函数，用来帮助计算dz：

如果 g(.)是激活函数, 那么sigmoid_backward 和 relu_backward 这样计算：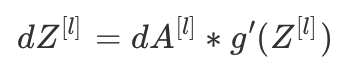

  • sigmoid_backward:实现了sigmoid（）函数的反向传播，用来计算dz为：
  1. dZ = sigmoid_backward(dA, activation_cache)
  • relu_backward: 实现了relu（）函数的反向传播，用来计算dz为：
  1. dZ = relu_backward(dA, activation_cache)

后向函数为：

  1. def sigmoid_backward(dA, cache):
  2.     """
  3.     Implement the backward propagation for a single SIGMOID unit.
  4.  
  5.     Arguments:
  6.     dA -- post-activation gradient, of any shape
  7.     cache -- 'Z' where we store for computing backward propagation efficiently
  8.  
  9.     Returns:
  10.     dZ -- Gradient of the cost with respect to Z
  11.     """
  12.  
  13.     Z = cache
  14.  
  15.     s = /(+np.exp(-Z))
  16.     dZ = dA * s * (-s)
  17.  
  18.     assert (dZ.shape == Z.shape)
  19.  
  20.     return dZ
  21.  
  22. def relu_backward(dA, cache):
  23.     """
  24.     Implement the backward propagation for a single RELU unit.
  25.  
  26.     Arguments:
  27.     dA -- post-activation gradient, of any shape
  28.     cache -- 'Z' where we store for computing backward propagation efficiently
  29.  
  30.     Returns:
  31.     dZ -- Gradient of the cost with respect to Z
  32.     """
  33.  
  34.     Z = cache
  35.     dZ = np.array(dA, copy=True) # just converting dz to a correct object.
  36.  
  37.     # When z <= , you should set dz to  as well.
  38.     dZ[Z <= ] = 
  39.  
  40.     assert (dZ.shape == Z.shape)
  41.  
  42.     return dZ

代码为：

  1. def linear_activation_backward(dA,cache,activation="relu"):
  2.     """
  3.     实现LINEAR-> ACTIVATION层的后向传播。
  4.  
  5.     参数：
  6.          dA - 当前层l的激活后的梯度值
  7.          cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache，activation_cache）
  8.          activation - 要在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
  9.     返回：
  10.          dA_prev - 相对于激活（前一层l-）的成本梯度值，与A_prev维度相同
  11.          dW - 相对于W（当前层l）的成本梯度值，与W的维度相同
  12.          db - 相对于b（当前层l）的成本梯度值，与b的维度相同
  13.     """
  14.     linear_cache, activation_cache = cache
  15.     #其实是先通过线性激活部分后向传播得到dz，然后再将dz带入线性部分的后向传播得到dw,db,dA_prev
  16.     if activation == "relu":
  17.         dZ = relu_backward(dA, activation_cache)
  18.         dA_prev, dW, db = linear_backward(dZ, linear_cache)
  19.     elif activation == "sigmoid":
  20.         dZ = sigmoid_backward(dA, activation_cache)
  21.         dA_prev, dW, db = linear_backward(dZ, linear_cache)
  22.  
  23.     return dA_prev,dW,db

测试函数为：

  1. def linear_activation_backward_test_case():
  2.     """
  3.     aL, linear_activation_cache = (np.array([[ 3.1980455 ,  7.85763489]]), ((np.array([[-1.02387576,  1.12397796], [-1.62328545,  0.64667545], [-1.74314104, -0.59664964]]), np.array([[ 0.74505627,  1.97611078, -1.24412333]]), ), np.array([[ 3.1980455 ,  7.85763489]])))
  4.     """
  5.     np.random.seed()
  6.     dA = np.random.randn(,) #后向传播的输入
  7.     A = np.random.randn(,) #存于cache中用于后向传播计算的值
  8.     W = np.random.randn(,)
  9.     b = np.random.randn(,)
  10.     Z = np.random.randn(,)
  11.     linear_cache = (A, W, b)
  12.     activation_cache = Z
  13.     linear_activation_cache = (linear_cache, activation_cache)
  14.  
  15.     return dA, linear_activation_cache

测试：

  1. #测试linear_activation_backward
  2. print("==============测试linear_activation_backward==============")
  3. AL, linear_activation_cache = testCases.linear_activation_backward_test_case()
  4.  
  5. dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
  6. print ("sigmoid:")
  7. print ("dA_prev = "+ str(dA_prev))
  8. print ("dW = " + str(dW))
  9. print ("db = " + str(db) + "\n")
  10.  
  11. dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
  12. print ("relu:")
  13. print ("dA_prev = "+ str(dA_prev))
  14. print ("dW = " + str(dW))
  15. print ("db = " + str(db))

返回：

  1. ==============测试linear_activation_backward==============
  2. sigmoid:
  3. dA_prev = [[ 0.11017994  0.01105339]
  4.  [ 0.09466817  0.00949723]
  5.  [-0.05743092 -0.00576154]]
  6. dW = [[ 0.10266786  0.09778551 -0.01968084]]
  7. db = [[-0.05729622]]
  8.  
  9. relu:
  10. dA_prev = [[ 0.44090989 -.        ]
  11.  [ 0.37883606 -.        ]
  12.  [-0.2298228   .        ]]
  13. dW = [[ 0.44513824  0.37371418 -0.10478989]]
  14. db = [[-0.20837892]]

6.更新参数

根据上面后向传播得到的dw,db,dA_prev来更新参数，其中 α 是学习率

函数：

  1. def update_parameters(parameters, grads, learning_rate):
  2.     """
  3.     使用梯度下降更新参数
  4.  
  5.     参数：
  6.      parameters - 包含你的参数的字典，即w和b
  7.      grads - 包含梯度值的字典，是L_model_backward的输出
  8.  
  9.     返回：
  10.      parameters - 包含更新参数的字典
  11.                    参数[“W”+ str（l）] = ...
  12.                    参数[“b”+ str（l）] = ...
  13.     """
  14.     L = len(parameters) // 2 #整除2，得到层数
  15.     for l in range(L):
  16.         parameters["W" + str(l + )] = parameters["W" + str(l + )] - learning_rate * grads["dW" + str(l + )]
  17.         parameters["b" + str(l + )] = parameters["b" + str(l + )] - learning_rate * grads["db" + str(l + )]
  18.  
  19.     return parameters

测试函数：

  1. def update_parameters_test_case():
  2.     """
  3.     parameters = {'W1': np.array([[ 1.78862847,  0.43650985,  0.09649747],
  4.         [-1.8634927 , -0.2773882 , -0.35475898],
  5.         [-0.08274148, -0.62700068, -0.04381817],
  6.         [-0.47721803, -1.31386475,  0.88462238]]),
  7.  'W2': np.array([[ 0.88131804,  1.70957306,  0.05003364, -0.40467741],
  8.         [-0.54535995, -1.54647732,  0.98236743, -1.10106763],
  9.         [-1.18504653, -0.2056499 ,  1.48614836,  0.23671627]]),
  10.  'W3': np.array([[-1.02378514, -0.7129932 ,  0.62524497],
  11.         [-0.16051336, -0.76883635, -0.23003072]]),
  12.  'b1': np.array([[ .],
  13.         [ .],
  14.         [ .],
  15.         [ .]]),
  16.  'b2': np.array([[ .],
  17.         [ .],
  18.         [ .]]),
  19.  'b3': np.array([[ .],
  20.         [ .]])}
  21.     grads = {'dW1': np.array([[ 0.63070583,  0.66482653,  0.18308507],
  22.         [ .        ,  .        ,  .        ],
  23.         [ .        ,  .        ,  .        ],
  24.         [ .        ,  .        ,  .        ]]),
  25.  'dW2': np.array([[ 1.62934255,  .        ,  .        ,  .        ],
  26.         [ .        ,  .        ,  .        ,  .        ],
  27.         [ .        ,  .        ,  .        ,  .        ]]),
  28.  'dW3': np.array([[-1.40260776,  .        ,  .        ]]),
  29.  'da1': np.array([[ 0.70760786,  0.65063504],
  30.         [ 0.17268975,  0.15878569],
  31.         [ 0.03817582,  0.03510211]]),
  32.  'da2': np.array([[ 0.39561478,  0.36376198],
  33.         [ 0.7674101 ,  0.70562233],
  34.         [ 0.0224596 ,  0.02065127],
  35.         [-0.18165561, -0.16702967]]),
  36.  'da3': np.array([[ 0.44888991,  0.41274769],
  37.         [ 0.31261975,  0.28744927],
  38.         [-0.27414557, -0.25207283]]),
  39.  'db1': 0.75937676204411464,
  40.  'db2': 0.86163759922811056,
  41.  'db3': -0.84161956022334572}
  42.     """
  43.     np.random.seed()
  44.     W1 = np.random.randn(,)
  45.     b1 = np.random.randn(,)
  46.     W2 = np.random.randn(,)
  47.     b2 = np.random.randn(,)
  48.     parameters = {"W1": W1,
  49.                   "b1": b1,
  50.                   "W2": W2,
  51.                   "b2": b2}
  52.     np.random.seed()
  53.     dW1 = np.random.randn(,)
  54.     db1 = np.random.randn(,)
  55.     dW2 = np.random.randn(,)
  56.     db2 = np.random.randn(,)
  57.     grads = {"dW1": dW1,
  58.              "db1": db1,
  59.              "dW2": dW2,
  60.              "db2": db2}
  61.  
  62.     return parameters, grads

测试：

  1. #测试update_parameters
  2. print("==============测试update_parameters==============")
  3. parameters, grads = testCases.update_parameters_test_case()
  4. parameters = update_parameters(parameters, grads, 0.1)
  5.  
  6. print ("W1 = "+ str(parameters["W1"]))
  7. print ("b1 = "+ str(parameters["b1"]))
  8. print ("W2 = "+ str(parameters["W2"]))
  9. print ("b2 = "+ str(parameters["b2"]))

返回：

  1. ==============测试update_parameters==============
  2. W1 = [[-0.59562069 -0.09991781 -2.14584584  1.82662008]
  3.  [-1.76569676 -0.80627147  0.51115557 -1.18258802]
  4.  [-1.0535704  -0.86128581  0.68284052  2.20374577]]
  5. b1 = [[-0.04659241]
  6.  [-1.28888275]
  7.  [ 0.53405496]]
  8. W2 = [[-0.55569196  0.0354055   1.32964895]]
  9. b2 = [[-0.84610769]]

7.整合函数——训练

开始训练数据并得到最优参数

  1. def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=,print_cost=False,isPlot=True):
  2.     """
  3.     实现一个两层的神经网络，【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
  4.     参数：
  5.         X - 输入的数据，维度为(n_x，例子数)
  6.         Y - 标签，向量，0为非猫，1为猫，维度为(,数量)
  7.         layers_dims - 层数的向量，维度为(n_y,n_h,n_y)
  8.         learning_rate - 学习率
  9.         num_iterations - 迭代的次数
  10.         print_cost - 是否打印成本值，每100次打印一次
  11.         isPlot - 是否绘制出误差值的图谱
  12.     返回:
  13.         parameters - 一个包含W1，b1，W2，b2的字典变量
  14.     """
  15.     np.random.seed()
  16.     grads = {}
  17.     costs = []
  18.     (n_x,n_h,n_y) = layers_dims
  19.  
  20.     """
  21.     初始化参数
  22.     """
  23.     parameters = initialize_parameters(n_x, n_h, n_y)
  24.  
  25.     W1 = parameters["W1"]
  26.     b1 = parameters["b1"]
  27.     W2 = parameters["W2"]
  28.     b2 = parameters["b2"]
  29.  
  30.     """
  31.     开始进行迭代
  32.     """
  33.     for i in range(,num_iterations):
  34.         #前向传播
  35.         A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
  36.         A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
  37.  
  38.         #计算成本
  39.         cost = compute_cost(A2,Y)
  40.  
  41.         #后向传播
  42.         ##初始化后向传播
  43.         dA2 = - (np.divide(Y, A2) - np.divide( - Y,  - A2))
  44.  
  45.         ##向后传播，输入：“dA2，cache2，cache1”。 输出：“dA1，dW2，db2;还有dA0（未使用），dW1，db1”。
  46.         dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
  47.         dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
  48.  
  49.         ##向后传播完成后的数据保存到grads
  50.         grads["dW1"] = dW1
  51.         grads["db1"] = db1
  52.         grads["dW2"] = dW2
  53.         grads["db2"] = db2
  54.  
  55.         #更新参数
  56.         parameters = update_parameters(parameters,grads,learning_rate)
  57.         W1 = parameters["W1"]
  58.         b1 = parameters["b1"]
  59.         W2 = parameters["W2"]
  60.         b2 = parameters["b2"]
  61.  
  62.         #打印成本值，如果print_cost=False则忽略
  63.         if i %  == :
  64.             #记录成本
  65.             costs.append(cost)
  66.             #是否打印成本值
  67.             if print_cost:
  68.                 print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
  69.     #迭代完成，根据条件绘制图
  70.     if isPlot:
  71.         plt.plot(np.squeeze(costs))
  72.         plt.ylabel('cost')
  73.         plt.xlabel('iterations (per tens)')
  74.         plt.title("Learning rate =" + str(learning_rate))
  75.         plt.show()
  76.  
  77.     #返回parameters
  78.     return parameters

我们现在开始加载数据集,图像数据集的处理可以参照吴恩达课后作业学习1-week2-homework-logistic

  1. train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
  2.  
  3. train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[], -).T
  4. test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[], -).T
  5.  
  6. train_x = train_x_flatten /
  7. train_y = train_set_y
  8. test_x = test_x_flatten /
  9. test_y = test_set_y

数据集加载完成，开始正式训练：

  1. n_x =
  2. n_h =
  3. n_y =
  4. layers_dims = (n_x,n_h,n_y)
  5.  
  6. parameters = two_layer_model(train_x, train_set_y, layers_dims = (n_x, n_h, n_y), num_iterations = , print_cost=True,isPlot=True)

返回：

  1. 第  次迭代，成本值为： 0.6930497356599891
  2. 第  次迭代，成本值为： 0.6464320953428849
  3. 第  次迭代，成本值为： 0.6325140647912678
  4. 第  次迭代，成本值为： 0.6015024920354665
  5. 第  次迭代，成本值为： 0.5601966311605748
  6. 第  次迭代，成本值为： 0.515830477276473
  7. 第  次迭代，成本值为： 0.47549013139433266
  8. 第  次迭代，成本值为： 0.4339163151225749
  9. 第  次迭代，成本值为： 0.40079775362038866
  10. 第  次迭代，成本值为： 0.3580705011323798
  11. 第  次迭代，成本值为： 0.33942815383664127
  12. 第  次迭代，成本值为： 0.30527536361962654
  13. 第  次迭代，成本值为： 0.2749137728213016
  14. 第  次迭代，成本值为： 0.2468176821061485
  15. 第  次迭代，成本值为： 0.19850735037466094
  16. 第  次迭代，成本值为： 0.17448318112556652
  17. 第  次迭代，成本值为： 0.17080762978096245
  18. 第  次迭代，成本值为： 0.11306524562164728
  19. 第  次迭代，成本值为： 0.09629426845937152
  20. 第  次迭代，成本值为： 0.08342617959726863
  21. 第  次迭代，成本值为： 0.07439078704319081
  22. 第  次迭代，成本值为： 0.06630748132267934
  23. 第  次迭代，成本值为： 0.05919329501038173
  24. 第  次迭代，成本值为： 0.05336140348560557
  25. 第  次迭代，成本值为： 0.048554785628770185

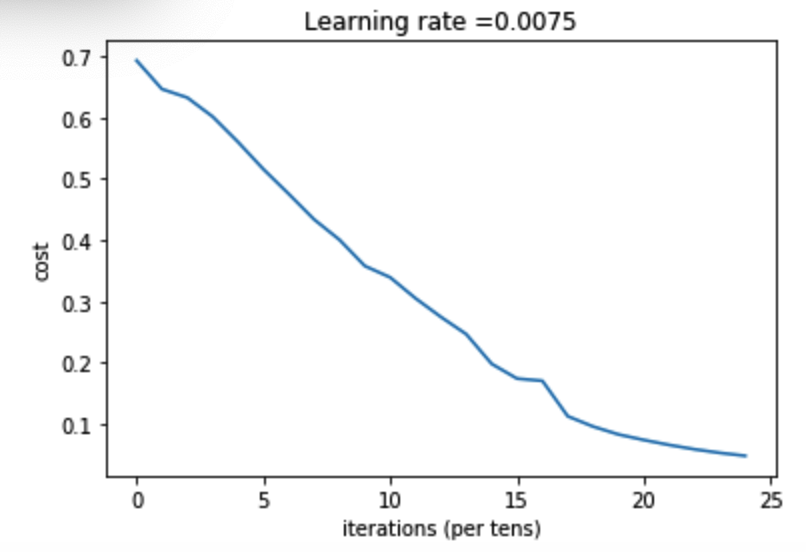
图示：

8.预测

  1. def predict(X, y, parameters):
  2.     """
  3.     该函数用于预测L层神经网络的结果，当然也包含两层
  4.  
  5.     参数：
  6.      X - 测试集
  7.      y - 标签
  8.      parameters - 训练模型得到的最优参数
  9.  
  10.     返回：
  11.      p - 给定数据集X的预测
  12.     """
  13.  
  14.     m = X.shape[]
  15.     n = len(parameters) // 2 # 神经网络的层数
  16.     p = np.zeros((,m))
  17.  
  18.     #根据参数前向传播
  19.     probas, caches = L_model_forward(X, parameters)
  20.  
  21.     for i in range(, probas.shape[]):
  22.         if probas[,i] > 0.5:
  23.             p[,i] =
  24.         else:
  25.             p[,i] = 
  26.  
  27.     print("准确度为: "  + str(float(np.sum((p == y))/m)))
  28.  
  29.     return p

预测函数构建好了我们就开始预测，查看训练集和测试集的准确性：

  1. predictions_train = predict(train_x, train_y, parameters) #训练集
  2. predictions_test = predict(test_x, test_y, parameters) #测试集

返回：

  1. 准确度为: 1.0
  2. 准确度为: 0.72

可见两层的训练效果比单层的logistic回归的效果要好一些

吴恩达课后作业学习1-week4-homework-two-hidden-layer -1的更多相关文章

  1. 吴恩达课后作业学习1-week4-homework-multi-hidden-layer -2

    参考:https://blog.csdn.net/u013733326/article/details/79767169 希望大家直接到上面的网址去查看代码,下面是本人的笔记 实现多层神经网络 1.准 ...

  2. 吴恩达课后作业学习2-week1-1 初始化

    参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 初始化.正则化.梯度校验 ...

  3. 吴恩达课后作业学习2-week1-2正则化

    参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 4.正则化 1)加载数据 ...

  4. 吴恩达课后作业学习1-week3-homework-one-hidden-layer

    参考:https://blog.csdn.net/u013733326/article/details/79702148 希望大家直接到上面的网址去查看代码,下面是本人的笔记 建立一个带有隐藏层的神经 ...

  5. 吴恩达课后作业学习1-week2-homework-logistic

    参考:https://blog.csdn.net/u013733326/article/details/79639509 希望大家直接到上面的网址去查看代码,下面是本人的笔记 搭建一个能够 “识别猫” ...

  6. 吴恩达课后作业学习2-week3-tensorflow learning-1-基本概念

    参考:https://blog.csdn.net/u013733326/article/details/79971488 希望大家直接到上面的网址去查看代码,下面是本人的笔记  到目前为止,我们一直在 ...

  7. 吴恩达课后作业学习2-week2-优化算法

    参考:https://blog.csdn.net/u013733326/article/details/79907419 希望大家直接到上面的网址去查看代码,下面是本人的笔记 我们需要做以下几件事:  ...

  8. 吴恩达课后作业学习2-week3-tensorflow learning-1-例子学习

    参考:https://blog.csdn.net/u013733326/article/details/79971488 使用TensorFlow构建你的第一个神经网络 我们将会使用TensorFlo ...

  9. 吴恩达课后作业学习2-week1-3梯度校验

    参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 5.梯度校验 在我们执行 ...

随机推荐

  1. 为什么用bower 安装bootstrap而不用npm来安装？

    NPM(node package manager),通常称为node包管理器.顾名思义,它的主要功能就是管理node包,包括:安装.卸载.更新.查看.搜索.发布等. npm的背后,是基于couchdb ...

  2. K8S 部署 ingress-nginx (一) 原理及搭建

    Kubernetes 暴露服务的有三种方式,分别为 LoadBlancer Service.NodePort Service.Ingress.官网对 Ingress 的定义为管理对外服务到集群内服务之 ...

  3. Android开发三种第三方图片加载的框架

    最近在项目中用到了大量图片加载,第三方优秀框架还不错,下面介绍三款榜首的框架用法和问题,做一个记录. 现在项目使用的是Android Studio开发的,现在也没有多少人使用Eclipse了吧. 一. ...

  4. Testlink1.9.17使用方法(第七章 测试用例集管理)

    第七章 测试用例集管理 QQ交流群:585499566 测试用例准备好以后,可以对测试用例集进行相关的操作. 一. 添加测试用例到测试计划中 在主页的“当前测试计划”下拉列表里-->选择一个测试 ...

  5. 章节七、1-ArrayList

    一.集合是一个容器,前面讲的数值也是一个容器, 它们的区别是: 1.数组既可以存储基本数据类型,又可以存储引用数据类型,而集合只能存储引用数据类型,也就是对象. 2.基本数据类型存储的是值,引用数据类 ...

  6. 【软件需求工程与建模 - 小组项目】第6周 - 成果展示3 - 软件设计规格说明书V4.1

    成果展示3 - 软件设计规格说明书V4.1

  7. Spark操作parquet文件

    package code.parquet import java.net.URI import org.apache.hadoop.conf.Configuration import org.apac ...

  8. 使用Visual Studio Team Services敏捷规划和项目组合管理（一）——使用团队、区域和迭代

    使用Visual Studio Team Services敏捷规划和项目组合管理(一)--使用团队.区域和迭代 概述 在本实验,你将会了解Visual Studio Team Services提供的敏 ...

  9. OSWatcher使用过程中小问题解决方法

    本文介绍一下在使用OSWatcher过程当中遇到的两个问题的解决方法.如有更好的方法,敬请留言. 1:OSWatcher在配置文件里面设置了参数OSW_COMPRESSION为gzip后,OSWatc ...

  10. FileInputStream、FileReader、FileWriter和File

    FileInputStream提供了对文件的字节读取 用于读取诸如图像数据之类的原始字节流       如:FileInputStream fis=new FileInputStream(new Fi ...