【[SDOI2017]序列计数】

感觉自己的复杂度感人

大概是\(O(p*\pi(m)+p^3logn)\)

还是能过去的

我们看到这么大的数据范围还是应该先想一想暴力怎么写

显然我们可以直接暴力\(dp\)

设\(dp[i][j]\)表示已经选择了\(i\)数，其中所有数的和\(mod\ p\)为\(j\)的方案数

显然方程是

\[f[i][j]=\sum_{k=1}^mdp[i-1][((j-k)\%p+p)\%p]
\]

初始的状态是\(dp[0][0]=1\)，最终的答案是\(dp[n][0]\)

至于还有一个至少有一个素数的限制条件，我们可以先不管这个条件直接算一遍，之后再保证\(k\)不为素数再算一遍，两个一减就是答案了

这样暴力转移的复杂度是\(O(nmp)\)的，于是我们要考虑优化

这个转移相当的固定，于是可以矩乘优化

我们发现因为\(p\)非常的小，于是那个膜\(p\)意义下的转移会有很多重复的位置被转移过去，于是我们如果可以预处理出这样一个数组\(tot[j][k]\)

表示\(dp[i-1][k]\)会向\(dp[i][k]\)专一多少次，也就是\(dp[i][k]+=dp[i-1][j]*tot[j][k]\)

于是就有这样一个矩阵会被构造出来

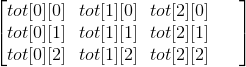
(\(p=3\)的情况)

于是就可以转移了，至于\(tot[j][k]\)怎么求，这个就是很简单了

在没有素数的情况下把所有素数对应的转移减一遍就好了

代码

#include<iostream>
#include<cstring>
#include<bitset>
#include<cstdio>
#define re register
#define maxn 20000005
#define LL long long
const LL mod=20170408;
std::bitset<maxn> f;
int prime[1500000];
LL ans[101][101],a[101][101];
int m,p;
LL n;
inline void did_a()
{
	LL mid[101][101];
	for(re int i=1;i<=p;i++)
		for(re int j=1;j<=p;j++)
			mid[i][j]=a[i][j],a[i][j]=0;
	for(re int i=1;i<=p;i++)
		for(re int j=1;j<=p;j++)
			for(re int k=1;k<=p;k++)
				a[i][j]=(a[i][j]+(mid[i][k]*mid[k][j])%mod)%mod;
}
inline void did_ans()
{
	LL mid[101][101];
	for(re int i=1;i<=p;i++)
		for(re int j=1;j<=p;j++)
			mid[i][j]=ans[i][j],ans[i][j]=0;
	for(re int i=1;i<=p;i++)
		for(re int j=1;j<=p;j++)
			for(re int k=1;k<=p;k++)
				ans[i][j]=(ans[i][j]+(mid[i][k]*a[k][j])%mod)%mod;
}
inline void Rebuild()
{
	memset(ans,0,sizeof(ans));
	memset(a,0,sizeof(a));
	for(re int i=1;i<=p;i++)
		ans[i][i]=1;
	int t=m/p;
	for(re int i=1;i<=p;i++)
		for(re int j=1;j<=p;j++)
			a[i][j]=t;
	int tot=m%p;
	for(re int i=1;i<=p;i++)
	{
		int cnt=tot,x=i-1;
		if(!x) x=p;
		while(cnt)
		{
			a[i][x]++,cnt--;
			x--;
			if(!x) x=p;
		}
	}
}
inline void out()
{
	for(re int i=1;i<=p;i++)
		{
			for(re int j=1;j<=p;j++)
			printf("%d ",a[i][j]);
			putchar(10);
		}
}
inline void quick(LL b)
{
	while(b)
	{
		if(b&1ll) did_ans();
		b>>=1ll;
		did_a();
	}
}
int main()
{
	scanf("%lld%d%d",&n,&m,&p);
	f[1]=1;
	for(re int i=2;i<=m;i++)
	{
		if(!f[i]) prime[++prime[0]]=i;
		for(re int j=1;j<=prime[0]&&prime[j]*i<=m;j++)
		{
			f[prime[j]*i]=i;
			if(i%prime[j]==0) break;
		}
	}
	Rebuild();
	quick(n);
	LL num=ans[1][1];
	Rebuild();
	for(re int i=1;i<=p;i++)
	{
		for(re int j=1;j<=prime[0];j++)
		{
			a[i][((i-1-prime[j])%p+p)%p+1]--;
			if(a[i][(i-prime[j]+p)%p+1]<0) a[i][(i-prime[j]+p)%p+1]=mod-1;
		}
	}
	quick(n);
	std::cout<<(num-ans[1][1]+mod)%mod;
	return 0;
}