UVa 10655 n次方之和（矩阵快速幂）

https://vjudge.net/problem/UVA-10655

题意：

输入非负整数p，q，n，求a^n+b^n的值，其中a和b满足a+b=p，ab=q。

思路：

递推式转化成矩阵的规律：

这道题目根据递推式是可以转化为矩阵的：

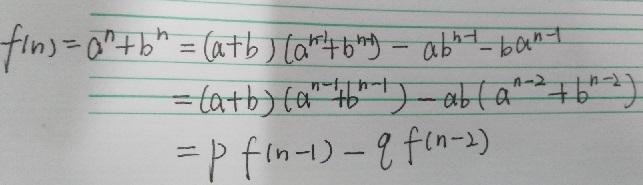
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<queue>
 #include<cmath>
 #include<map>
 using namespace std;

 typedef long long LL;

 LL p,q,n;

 struct Matrix
 {
     LL m[][];
 }ans,base;

 Matrix multi(Matrix a,Matrix b)
 {
     Matrix temp;
     for(int i=;i<;i++)
     for(int j=;j<;j++)
     {
         temp.m[i][j]=;
        for(int k=;k<;k++)
        {
           temp.m[i][j]=(temp.m[i][j]+a.m[i][k]*b.m[k][j]);
        }
     }
     return temp;
 }

 void pow(int x)
 {
     ans.m[][]=ans.m[][]=;
     ans.m[][]=ans.m[][]=;
     base.m[][]=;
     base.m[][]=;
     base.m[][]=-q;
     base.m[][]=p;
     while(x)
     {
         if(x&)
         {
             ans=multi(ans,base);
         }
         base=multi(base,base);
         x>>=;
     }
     printf("%lld\n",ans.m[][]*p+*ans.m[][]);
 }

 int main()
 {
     //freopen("D:\\input.txt","r",stdin);
     while(scanf("%lld%lld%lld",&p,&q,&n)==)
     {
         if(n==)   {puts("");continue;}
         if(n==)   {printf("%lld\n",p);continue;}
         if(n==)   {printf("%lld\n",p*p-*q);continue;}
         pow(n-);
     }
     return ;
 }