4、2支持向量机SVM算法实践

支持向量机SVM算法实践

　　利用Python构建一个完整的SVM分类器，包含SVM分类器的训练和利用SVM分类器对未知数据的分类，

一、训练SVM模型

　　首先构建SVM模型相关的类

 class SVM:
     def __init__(self, dataSet, labels, C, toler, kernel_option):
         self.train_x = dataSet  # 训练特征
         self.train_y = labels  # 训练标签
         self.C = C  # 惩罚参数
         self.toler = toler  # 迭代的终止条件之一
         self.n_samples = np.shape(dataSet)[0]  # 训练样本的个数
         self.alphas = np.mat(np.zeros((self.n_samples, 1)))  # 拉格朗日乘子
         self.b = 0
         self.error_tmp = np.mat(np.zeros((self.n_samples, 2)))  # 保存E的缓存
         self.kernel_opt = kernel_option  # 选用的核函数及其参数
         self.kernel_mat = calc_kernel(self.train_x, self.kernel_opt)  # 核函数的输出

其中，calc_kernel函数用于根据指定的核函数kernel_opt计算样本的核函数矩阵，

calc_kernel函数的具体实现如下：

 def calc_kernel(train_x, kernel_option):
     '''计算核函数矩阵
     input:  train_x(mat):训练样本的特征值
             kernel_option(tuple):核函数的类型以及参数
     output: kernel_matrix(mat):样本的核函数的值
     '''
     m = np.shape(train_x)[0]  # 样本的个数
     kernel_matrix = np.mat(np.zeros((m, m)))  # 初始化样本之间的核函数值
     for i in range(m):
         kernel_matrix[:, i] = cal_kernel_value(train_x, train_x[i, :],kernel_option)
     return kernel_matrix

在程序中，calc_kernel函数用于根据指定的核函数数类型以及参数kernel_option计算最终的样本和函数矩阵，样本核函数矩阵为：

　　                         

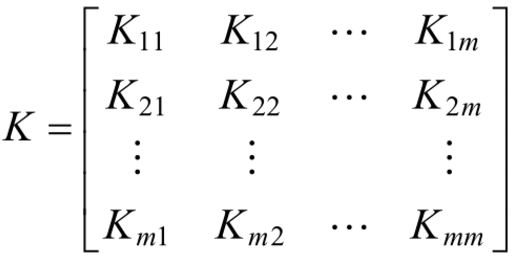
　　其中，K_i，j表示的是第i个样本和第j个样本之间的核函数的值，在计算的过程中，利用cal_kernel_value函数计算每一个样本与其他样本的核函数的值。

函数cal_kernel_value的具体实现代码：

 def cal_kernel_value(train_x, train_x_i, kernel_option):
     '''样本之间的核函数的值
     input:  train_x(mat):训练样本
             train_x_i(mat):第i个训练样本
             kernel_option(tuple):核函数的类型以及参数
     output: kernel_value(mat):样本之间的核函数的值

     '''
     kernel_type = kernel_option[0]  # 核函数的类型，分为rbf和其他
     m = np.shape(train_x)[0]  # 样本的个数

     kernel_value = np.mat(np.zeros((m, 1)))

     if kernel_type == 'rbf':  # rbf核函数
         sigma = kernel_option[1]
         if sigma == 0:
             sigma = 1.0
         for i in range(m):
             diff = train_x[i, :] - train_x_i
             kernel_value[i] = np.exp(diff * diff.T / (-2.0 * sigma ** 2))
     else:  # 不使用核函数
         kernel_value = train_x * train_x_i.T
     return kernel_value

cal_kernel_value函数用于根据指定的核函数类型以及参数kernel_option计算样本train_x_i与其他所有样本之间的核函数的值，在实现过程中只实现了高斯核函数。若没有指定和函数的类型，则默认不使用核函数。

　　当定义好SVM模型后，我们需要完成SVN模型的最重要的功能，即利用SMO算法对SVM模型进行训练，训练SVM模型的具体过程如下：

 def SVM_training(train_x, train_y, C, toler, max_iter, kernel_option=('rbf', 0.431029)):
     '''SVM的训练
     input:  train_x(mat):训练数据的特征
             train_y(mat):训练数据的标签
             C(float):惩罚系数
             toler(float):迭代的终止条件之一
             max_iter(int):最大迭代次数
             kerner_option(tuple):核函数的类型及其参数
     output: svm模型
     '''
     # 1、初始化SVM分类器
     svm = SVM(train_x, train_y, C, toler, kernel_option)

     # 2、开始训练
     entireSet = True
     alpha_pairs_changed = 0
     iteration = 0

     while (iteration < max_iter) and ((alpha_pairs_changed > 0) or entireSet):
         print
         "\t iterration: ", iteration
         alpha_pairs_changed = 0

         if entireSet:
             # 对所有的样本
             for x in range(svm.n_samples):
                 alpha_pairs_changed += choose_and_update(svm, x)
             iteration += 1
         else:
             # 非边界样本
             bound_samples = []
             for i in range(svm.n_samples):
                 if svm.alphas[i, 0] > 0 and svm.alphas[i, 0] < svm.C:
                     bound_samples.append(i)
             for x in bound_samples:
                 alpha_pairs_changed += choose_and_update(svm, x)
             iteration += 1

         # 在所有样本和非边界样本之间交替
         if entireSet:
             entireSet = False
         elif alpha_pairs_changed == 0:
             entireSet = True

     return svm

函数SVM_training通过在非边界样本或所有样本中交替遍历，选择出第一个需要优化的αi，优先选择遍历非边界样本，因为非边界样本更有可能需要调整，而边界样本常常不能得到进一步调整而留在边界。循环遍历非边界样本并选出它们当中违反KKT条件的样本进行调整，直到非边界样本全部满足KKT条件为止。当某一次遍历发现没有非边界样本得到调整时，就遍历所有样本，已检验是否整个几何都满足KKT条件。如果Zaire整个集合的检验中又有样本被进一步优化，就有必要在遍历非边界样本。这样不停的遍历所有样本和遍历非边界样本之间切换，直到整个训练样本集都满足KKT条件为止。在选择出第一个变量αi后，需要判断其是否满足条件，同时，需要选择第二个变量αj，这个过程的实现代码为choose_and_update

 def choose_and_update(svm, alpha_i):
     '''判断和选择两个alpha进行更新
     input:  svm:SVM模型
             alpha_i(int):选择出的第一个变量
     '''
     error_i = cal_error(svm, alpha_i)  # 计算第一个样本的E_i

     # 判断选择出的第一个变量是否违反了KKT条件
     if (svm.train_y[alpha_i] * error_i < -svm.toler) and (svm.alphas[alpha_i] < svm.C) or \
             (svm.train_y[alpha_i] * error_i > svm.toler) and (svm.alphas[alpha_i] > 0):

         # 1、选择第二个变量
         alpha_j, error_j = select_second_sample_j(svm, alpha_i, error_i)
         alpha_i_old = svm.alphas[alpha_i].copy()
         alpha_j_old = svm.alphas[alpha_j].copy()

         # 2、计算上下界
         if svm.train_y[alpha_i] != svm.train_y[alpha_j]:
             L = max(0, svm.alphas[alpha_j] - svm.alphas[alpha_i])
             H = min(svm.C, svm.C + svm.alphas[alpha_j] - svm.alphas[alpha_i])
         else:
             L = max(0, svm.alphas[alpha_j] + svm.alphas[alpha_i] - svm.C)
             H = min(svm.C, svm.alphas[alpha_j] + svm.alphas[alpha_i])
         if L == H:
             return 0

         # 3、计算eta
         eta = 2.0 * svm.kernel_mat[alpha_i, alpha_j] - svm.kernel_mat[alpha_i, alpha_i] \
               - svm.kernel_mat[alpha_j, alpha_j]
         if eta >= 0:
             return 0

         # 4、更新alpha_j
         svm.alphas[alpha_j] -= svm.train_y[alpha_j] * (error_i - error_j) / eta

         # 5、确定最终的alpha_j
         if svm.alphas[alpha_j] > H:
             svm.alphas[alpha_j] = H
         if svm.alphas[alpha_j] < L:
             svm.alphas[alpha_j] = L

         # 6、判断是否结束
         if abs(alpha_j_old - svm.alphas[alpha_j]) < 0.00001:
             update_error_tmp(svm, alpha_j)
             return 0

         # 7、更新alpha_i
         svm.alphas[alpha_i] += svm.train_y[alpha_i] * svm.train_y[alpha_j] \
                                * (alpha_j_old - svm.alphas[alpha_j])

         # 8、更新b
         b1 = svm.b - error_i - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) \
              * svm.kernel_mat[alpha_i, alpha_i] \
              - svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) \
              * svm.kernel_mat[alpha_i, alpha_j]
         b2 = svm.b - error_j - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) \
              * svm.kernel_mat[alpha_i, alpha_j] \
              - svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) \
              * svm.kernel_mat[alpha_j, alpha_j]
         if (0 < svm.alphas[alpha_i]) and (svm.alphas[alpha_i] < svm.C):
             svm.b = b1
         elif (0 < svm.alphas[alpha_j]) and (svm.alphas[alpha_j] < svm.C):
             svm.b = b2
         else:
             svm.b = (b1 + b2) / 2.0

         # 9、更新error
         update_error_tmp(svm, alpha_j)
         update_error_tmp(svm, alpha_i)

         return 1
     else:
         return 0

函数choose_and_update实现了SMO中最核心的部分，在函数choose_and_update中，首先，判断选择出的第一个变量αi是否满足要求，在判断的过程中需要计算第一个变量的误差值E_i，使用函数cal_reeor计算变量的误差值，当检查第一个变量αi满足条件后，需要现在第二个变量α_j，对于第二个变量，选择的标准是使得其改变最大，选择的具体过程使用select_second_sample_j函数来具体实现，当两个变量αi和α_j都跟新完成后，此时需要重新计算b的值如svm.b = (b1+b2)/2.0。最终，需要重新计算两个变量αi和α_j对应的误差值Ei和Ej。

函数cal_error：

 def cal_error(svm, alpha_k):
     '''误差值的计算
     input:  svm:SVM模型
             alpha_k(int):选择出的变量
     output: error_k(float):误差值
     '''
     output_k = float(np.multiply(svm.alphas, svm.train_y).T * svm.kernel_mat[:, alpha_k] + svm.b)
     error_k = output_k - float(svm.train_y[alpha_k])
     return error_k

函数select_second_sample_j：

 def select_second_sample_j(svm, alpha_i, error_i):
     '''选择第二个样本
     input:  svm:SVM模型
             alpha_i(int):选择出的第一个变量
             error_i(float):E_i
     output: alpha_j(int):选择出的第二个变量
             error_j(float):E_j
     '''
     # 标记为已被优化
     svm.error_tmp[alpha_i] = [1, error_i]
     candidateAlphaList = np.nonzero(svm.error_tmp[:, 0].A)[0]

     maxStep = 0
     alpha_j = 0
     error_j = 0

     if len(candidateAlphaList) > 1:
         for alpha_k in candidateAlphaList:
             if alpha_k == alpha_i:
                 continue
             error_k = cal_error(svm, alpha_k)
             if abs(error_k - error_i) > maxStep:
                 maxStep = abs(error_k - error_i)
                 alpha_j = alpha_k
                 error_j = error_k
     else:  # 随机选择
         alpha_j = alpha_i
         while alpha_j == alpha_i:
             alpha_j = int(np.random.uniform(0, svm.n_samples))
         error_j = cal_error(svm, alpha_j)

     return alpha_j, error_j

函数update_error_tmp：

 def update_error_tmp(svm, alpha_k):
     '''重新计算误差值
     input:  svm:SVM模型
             alpha_k(int):选择出的变量
     output: 对应误差值
     '''
     error = cal_error(svm, alpha_k)
     svm.error_tmp[alpha_k] = [1, error]

上述代码为构建SVM模型，存在SVM.py文件中，现在要训练SVM，我们建立“svm_train.py”文件。首先，导入svm文件：

# coding:UTF-8
import numpy as np
import svm

SVM训练模型的主函数：

　　

if __name__ == "__main__":
    # 1、导入训练数据
    print("------------ 1、load data --------------")
    dataSet, labels = load_data_libsvm("resource/heart_scale")
    # 2、训练SVM模型
    print("------------ 2、training ---------------")
    C = 0.6
    toler = 0.001
    maxIter = 500
    svm_model = svm.SVM_training(dataSet, labels, C, toler, maxIter)
    # 3、计算训练的准确性
    print("------------ 3、cal accuracy --------------")
    accuracy = svm.cal_accuracy(svm_model, dataSet, labels)
    print(type(svm_model))
    print("The training accuracy is: %.3f%%" % (accuracy * 100))
    # 4、保存最终的SVM模型
    print("------------ 4、save model ----------------")
    svm.save_svm_model(svm_model, "model_file")

主要分为四个部分：

1.使用loda_data_libsvm函数导入训练数据

2.调用svm.py文件中的SVM_training函数对SVM模型进行模型训练

3.利用svm.py文件中的cal_accuracy函数对模型准确性进行评估

4.利用svm.py文件中的save_model函数将最终的svm模型保存到指定额目录

load_data_libsvm函数：

 def load_data_libsvm(data_file):
     '''导入训练数据
     input:  data_file(string):训练数据所在文件
     output: data(mat):训练样本的特征
             label(mat):训练样本的标签
     '''
     data = []
     label = []
     f = open(data_file)
     for line in f.readlines():
         lines = line.strip().split(' ')

         # 提取得出label
         label.append(float(lines[0]))
         # 提取出特征，并将其放入到矩阵中
         index = 0
         tmp = []
         for i in range(1, len(lines)):
             li = lines[i].strip().split(":")
             if int(li[0]) - 1 == index:
                 tmp.append(float(li[1]))
             else:
                 while (int(li[0]) - 1 > index):
                     tmp.append(0)
                     index += 1
                 tmp.append(float(li[1]))
             index += 1
         while len(tmp) < 13:
             tmp.append(0)
         data.append(tmp)
     f.close()
     return np.mat(data), np.mat(label).T

cal_accuracy函数计算SVM模型的准确率：

 def cal_accuracy(svm, test_x, test_y):
     '''计算预测的准确性
     input:  svm:SVM模型
             test_x(mat):测试的特征
             test_y(mat):测试的标签
     output: accuracy(float):预测的准确性
     '''
     n_samples = np.shape(test_x)[0]  # 样本的个数
     correct = 0.0
     for i in range(n_samples):
         # 对每一个样本得到预测值
         predict = svm_predict(svm, test_x[i, :])
         # 判断每一个样本的预测值与真实值是否一致
         if np.sign(predict) == np.sign(test_y[i]):
             correct += 1
     accuracy = correct / n_samples
     return accuracy

svm_predict：函数对每一个样本预测：

 def svm_predict(svm, test_sample_x):
     '''利用SVM模型对每一个样本进行预测
     input:  svm:SVM模型
             test_sample_x(mat):样本
     output: predict(float):对样本的预测
     '''
     # 1、计算核函数矩阵
     kernel_value = cal_kernel_value(svm.train_x, test_sample_x, svm.kernel_opt)
     # 2、计算预测值
     predict = kernel_value.T * np.multiply(svm.train_y, svm.alphas) + svm.b
     return predict

save_svm_model：保存SVM模型：

 def save_svm_model(svm_model, model_file):
     '''保存SVM模型
     input:  svm_model:SVM模型
             model_file(string):SVM模型需要保存到的文件
     '''
     with open(model_file, 'wb') as f:
         pickle.dump(svm_model, f)

训练过程：

二、利用训练好的SVM模型对新的数据精心预测：

　　对于分类算法而言，训练好的模型需要能够对新的数据集进行划分。利用上述的训练好的SVM模型，并将其保存到了“model_file”文件中，此时，我们需要利用训练好的模型精心预测。

导入模块：

 # coding:UTF-8
 import numpy as np
 import pickle
 from svm import svm_predict

对新数据预测的主函数：

 if __name__ == "__main__":
     # 1、导入测试数据
     print("--------- 1.load data ---------")
     test_data = load_test_data("resource/svm_test_data")
     # 2、导入SVM模型
     print("--------- 2.load model ----------")
     svm_model = load_svm_model("model_file")
     # 3、得到预测值
     print("--------- 3.get prediction ---------")
     prediction = get_prediction(test_data, svm_model)
     # 4、保存最终的预测值
     print("--------- 4.save result ----------")
     save_prediction("result", prediction)

1.导入测试数据

2.导入SVM模型

3.计算得到预测值

4.保存预测值

导入测试数据集：

 def load_test_data(test_file):
     '''导入测试数据
     input:  test_file(string):测试数据
     output: data(mat):测试样本的特征
     '''
     data = []
     f = open(test_file)
     for line in f.readlines():
         lines = line.strip().split(' ')

         # 处理测试样本中的特征
         index = 0
         tmp = []
         for i in range(0, len(lines)):
             li = lines[i].strip().split(":")
             if int(li[0]) - 1 == index:
                 tmp.append(float(li[1]))
             else:
                 while (int(li[0]) - 1 > index):
                     tmp.append(0)
                     index += 1
                 tmp.append(float(li[1]))
             index += 1
         while len(tmp) < 13:
             tmp.append(0)
         data.append(tmp)
     f.close()
     return np.mat(data)

导入SVM模型：

 def load_svm_model(svm_model_file):
     '''导入SVM模型
     input:  svm_model_file(string):SVM模型保存的文件
     output: svm_model:SVM模型
     '''
     with open(svm_model_file, 'rb') as f:
         svm_model = pickle.load(f)
     return svm_model

对新数据精心预测：

 def get_prediction(test_data, svm):
     '''对样本进行预测
     input:  test_data(mat):测试数据
             svm:SVM模型
     output: prediction(list):预测所属的类别
     '''
     m = np.shape(test_data)[0]
     prediction = []
     for i in range(m):
         # 对每一个样本得到预测值
         predict = svm_predict(svm, test_data[i, :])
         # 得到最终的预测类别
         prediction.append(str(np.sign(predict)[0, 0]))
     return prediction

保存预测结果：

 def save_prediction(result_file, prediction):
     '''保存预测的结果
     input:  result_file(string):结果保存的文件
             prediction(list):预测的结果
     '''
     f = open(result_file, 'w')
     f.write(" ".join(prediction))
     f.close()

输出的预测结果文件