最短路径Dijkstar算法和Floyd算法详解（c语言版）

博客转载自：https://blog.csdn.net/crescent__moon/article/details/16986765

先说说Dijkstra吧，这种算法只能求单源最短路径，那么什么是单源最短路径呢？就是只能求一个点到别的点最短路径，而不能求所有点到其它点的最短路径。当然如果枚举所有点都用一遍Dijkstra的话，也能求出来，不过这就失去了这个算法的真正意义，而且时间复杂度会从O(n^2)变为O(n^3)。这个算法还有一个缺点就是在图中权值必须都是正的，否则不能用。下面说说Dijkstra的实现，首先你得有一个要求的源点和终点，然后有图，如果图之间没有直接连边，则初始化它们的权值为inf，如果两点相同，则权值为0，当然这是用邻接矩阵存的图，确保存的边是最短的。然后你得有两个数组来维护，一个是vis数组，用来判断节点是否被访问过，另一个是dis数组，用来存储其余点到源点的最短路径。初始化时，将vis数组全部设为false，dis数组为图中源点到各个点的距离，如果没有直接路径，则为inf。好了，初始化结束了，要开始实现了，要确保每个点都被访问过，所以除了源点之外，还有n-1个点，所以要遍历这n-1个点。每一次从这些点中找出vis是false的，也就是没有被访问过的，而且从这些中在找出到源点最近的那个点，设为v，然后标记v的vis为true，然后以这个v点开始，遍历与p点相邻的点，并且这些相邻的的点还要确保都没有访问过（vis为false）。然后这个算法关键之处就到来了，对这些与v相邻的顶点设为w，依次判读dis[v]的值+c(v，w)(代表v到w的直接可达的路径）是否小于dis[w]，如果小于，则更新dis[w]的值。至此为止，就是Dijksta算法。

以这个图为例来演示一遍这个算法的实现：以a为源点，求a到其它点的最短路径。

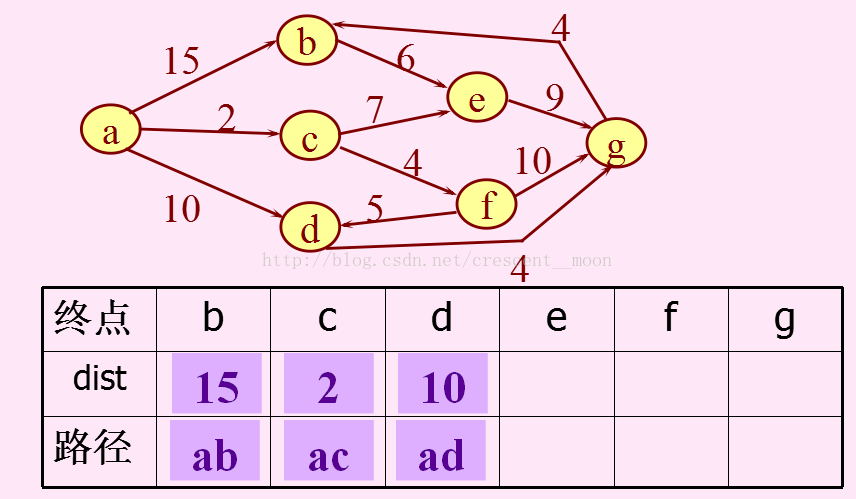
然后找与adist最近的，即c点，然后以c点开始遍历与其相邻的节点e和f，并更新它们的dist和路径。

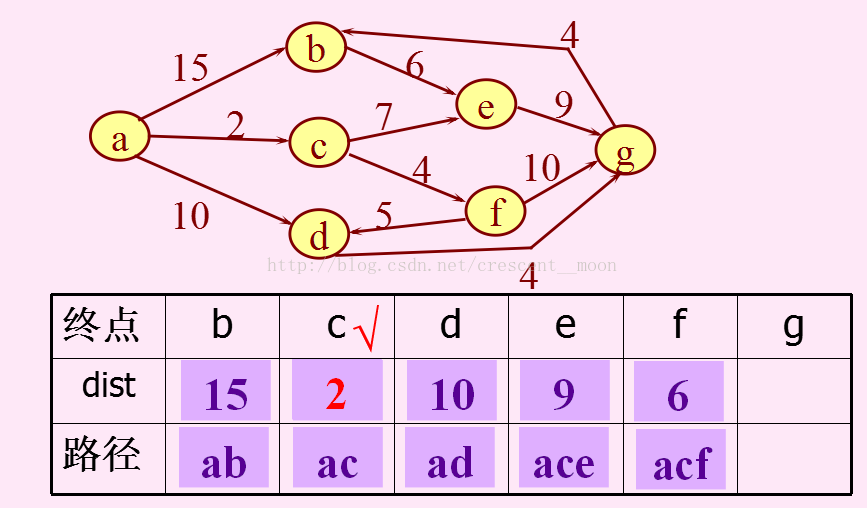
c点vis标记为true了，然后找vis标记为false的且dist最小的，也就是f点，遍历与f点相邻的邻接点且vis为false，也就是g和d点。

所以f点也访问完了，vis标记为true，然后接下来找的点，大家也能一眼看出是找e点了，然后遍历g点。

接下来访问d点。

在访问g点。

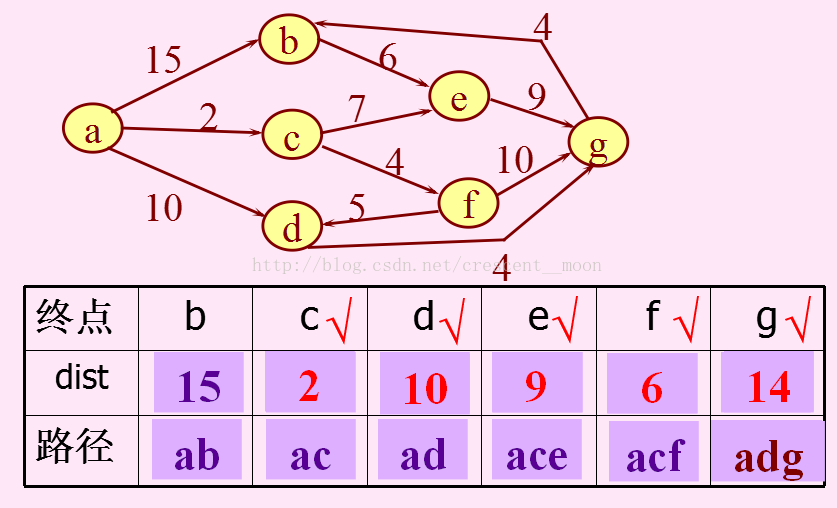
最后访问b点。

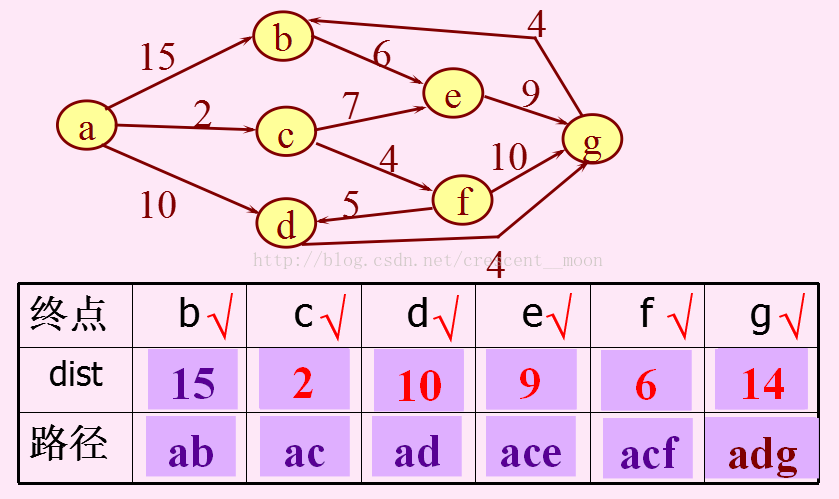
这就是此算法的实现。伪代码是：

void dijkstra(int u)//u为源点
{
    for(int i=1; i<=n; i++)
    {
        dist[i]=map[u][i];
        vis[i]=0;
    }
    dist[u]=0;
    vis[u]=1;
    for(int i=2; i<=n; i++)
    {
        int pos=0,min=inf;
        for(j=1; j<=n; j++)
            if(!vis[j]&&dist[j]<min)
            {
                pos=j;
                min=dist[j];
            }
        vis[pos]=1;
        for(j=1; j<=n; j++)
        {
            if(!vis[j]&&dis[j]>dis[pos]+map[pos][j])
            {
                dis[j]=dis[pos]+map[pos][j]
                pre[j]=pos;//记录其前驱
            }
        }
    }
}

Floyd算法求的是所有点之间的最短路径，并且可以处理权值为负值的边，时间复杂度为O(n^3)。

定义Dk,i,j为从vi到vj只使用v1,v2,…,vk作为中间顶点的最短路径的权。根据这个定义，D0,i,j=ci,j，其中若(vi,vj)不是该图的边，则ci,j=∞。并且，根据定义，D|v|,i,j是图中从vi到vj的最短路径。Floyd算法的基本思想是动态规划，1、求出顶点Vi和Vj不经过任何顶点的最短路径，路径的长度就是二者之间边的权重，表示为：P(0，i,j)=C(i,j)。

2、当求出P(k-1,i,j) 后，即Vi到Vj经过V1到Vk-1中的某些顶点的最短路径。则：Vi到Vj的中间经过V1到Vk中某些顶点的最短路径P(k,i,j)。

图的表示为：

下面以一个例子来说明它的实现：这是初始时的情况

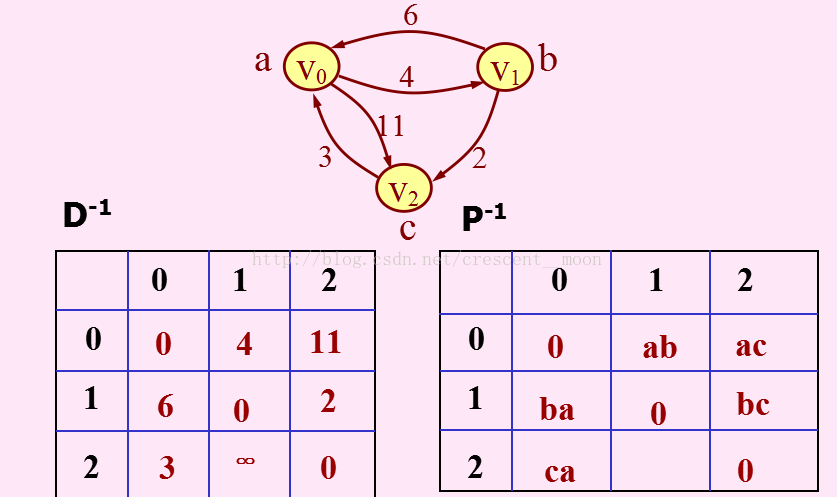
当k=0时，

当k=1时：

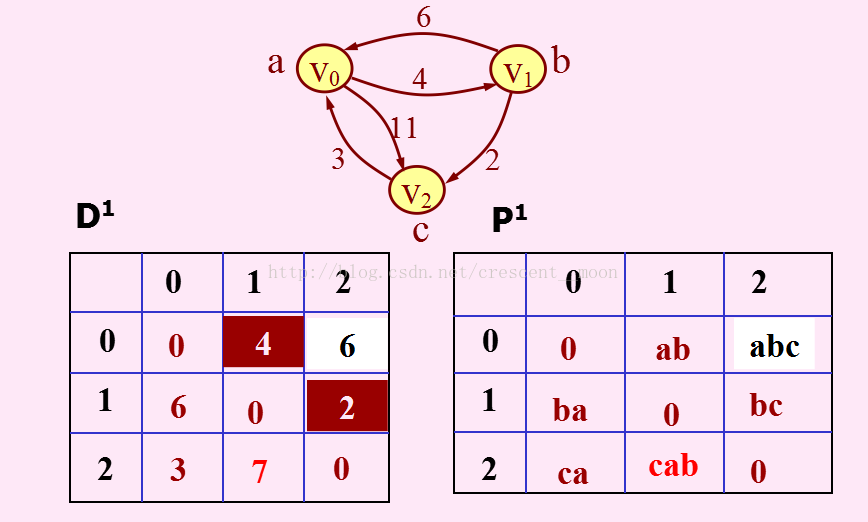
当k=2时：

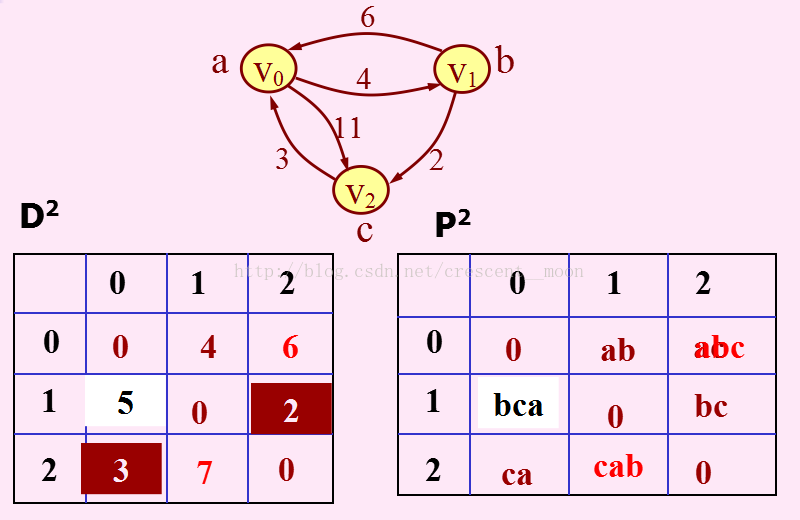
至此为止，此算法就结束了，图中的值即为任意两点间的最短距离。

Floyd的伪代码是：

for(k=1;k<=n;k++)
            for(i=1;i<=n;i++)
                for(j=1;j<=n;j++)
                {
                    if(map[i][k]+map[k][j]<map[i][j])
                    map[i][j]=map[i][k]+map[k][j];
                }