Guava源码学习（二）Ordering

基于版本：Guava 22.0

Wiki：Ordering

0. Ordering简介

Guava的Ordering提供了链式风格的比较器的实现，我们可以用Ordering轻松构建复杂的比较器。

1. 类图

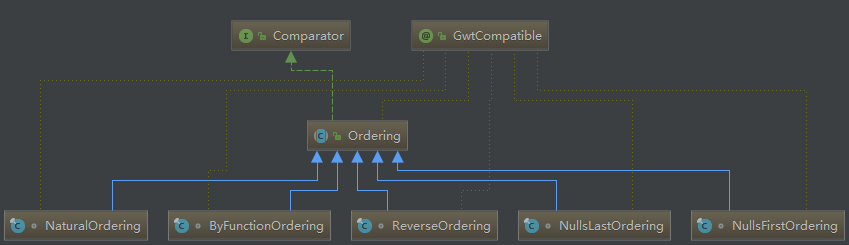
这张类图不完全，实际上Ordering有十几个子类，这些子类共同提供了复杂的功能。

2. 设计思路

Ordering是继承于java.util.Comparator接口的抽象类，它的十几个子类都实现了compare与equals方法，这些子类可以实现基本的排序功能。

通过链式调用，可以将这些子类组合在一起，实现复杂的排序规则。

举个例子：

Ordering combineOrdering = Ordering.natural().reverse().nullsFirst();

对应的源码如下

Ordering.nullsFirst()
  @GwtCompatible(serializable = true)
  public <S extends T> Ordering<S> nullsFirst() {
    return new NullsFirstOrdering<S>(this);
  }

Ordering.reverse()
  @GwtCompatible(serializable = true)
  public <S extends T> Ordering<S> reverse() {
    return new ReverseOrdering<S>(this);
  }

NullsFirstOrdering.class
  final Ordering<? super T> ordering;

  NullsFirstOrdering(Ordering<? super T> ordering) {
    this.ordering = ordering;
  }

  @Override
  public int compare(@Nullable T left, @Nullable T right) {
    if (left == right) {
      return 0;
    }
    if (left == null) {
      return RIGHT_IS_GREATER;
    }
    if (right == null) {
      return LEFT_IS_GREATER;
    }
    return ordering.compare(left, right);
  }

ReverseOrdering.class
  final Ordering<? super T> forwardOrder;

  ReverseOrdering(Ordering<? super T> forwardOrder) {
    this.forwardOrder = checkNotNull(forwardOrder);
  }

  @Override
  public int compare(T a, T b) {
    return forwardOrder.compare(b, a);
  }

可以看出combineOrdering实际上是由外部的NullsFirstOrdering加上内部ReverseOrdering嵌套而成的

在调用combineOrdering.compare方法的时候，会先调用NullsFirstOrdering.compare方法，再调用ReverseOrdering.compare方法

这会导致排序完毕的集合，null元素在最前面，后面则是逆向元素

比方[2,1,3,null,0]的排序结果就是[null,3,2,1,0]

这就是链式调用的特点，从右向左，逐渐应用排序规则。

3. CompoundOrdering

设想一个场景，我们需要对学生的月考成绩从高到低进行排序，如果两人分数相同，则按照学号排序。

很显然这两个规则对应于两个简单的比较器，但是如何将这两个排序规则结合起来呢？

此时我们需要CompoundOrdering

Ordering.compound方法会创建CompoundOrdering的实例，相关源码如下

Ordering.compound()
  public <U extends T> Ordering<U> compound(Comparator<? super U> secondaryComparator) {
    return new CompoundOrdering<U>(this, checkNotNull(secondaryComparator));
  }

  public static <T> Ordering<T> compound(Iterable<? extends Comparator<? super T>> comparators) {
    return new CompoundOrdering<T>(comparators);
  }

CompoundOrdering.class
  final ImmutableList<Comparator<? super T>> comparators;

  CompoundOrdering(Comparator<? super T> primary, Comparator<? super T> secondary) {
    this.comparators = ImmutableList.<Comparator<? super T>>of(primary, secondary);
  }

  CompoundOrdering(Iterable<? extends Comparator<? super T>> comparators) {
    this.comparators = ImmutableList.copyOf(comparators);
  }

  @Override
  public int compare(T left, T right) {
    // Avoid using the Iterator to avoid generating garbage (issue 979).
    int size = comparators.size();
    for (int i = 0; i < size; i++) {
      int result = comparators.get(i).compare(left, right);
      if (result != 0) {
        return result;
      }
    }
    return 0;
  }

很容易可以看出，CompoundOrdering内部维护了一个比较器列表，调用CompoundOrdering.compare方法时，会从头遍历这个列表，直到找到一个compare方法不返回0的比较器为止。

这样就实现了如果前面的比较器无法区分大小则调用后续的比较器进一步区分的语义。

与第二节讲到的链式调用的从右向左阅读规则不同的是，CompoundOrdering的阅读规则是从左向右。

Wiki上还特意提到(Exception to the "backwards" rule: For chains of calls to compound, read from left to right. To avoid confusion, avoid intermixing compound calls with other chained calls.) 为了避免理解上的混乱，请不要把compound写在一长串链式调用的中间，你可以另起一行，在链中最先或最后调用compound。

4. ByFunctionOrdering

Ordering的onResultOf方法提供了对先对集合内元素调用函数，然后再调用自定义比较器的解决方案

Ordering.onResultOf
  public <F> Ordering<F> onResultOf(Function<F, ? extends T> function) {
    return new ByFunctionOrdering<F, T>(function, this);
  }

ByFunctionOrdering.class
final class ByFunctionOrdering<F, T> extends Ordering<F> implements Serializable {
  final Function<F, ? extends T> function;
  final Ordering<T> ordering;

  ByFunctionOrdering(Function<F, ? extends T> function, Ordering<T> ordering) {
    this.function = checkNotNull(function);
    this.ordering = checkNotNull(ordering);
  }

  @Override
  public int compare(F left, F right) {
    return ordering.compare(function.apply(left), function.apply(right));
  }

代码非常简单，构造器中传入函数function与自定义比较器，然后compare方法中调用自定义比较器，对被function处理过的对象进行比较排序

举个例子，我们现在有一个实体类Student，里面有两个属性：String型的name，与Integer型的grade，现在我们需要对一个Student列表按照grade从高到低排序。

需要的比较器如下

    public static void main(String[] args) {
        Ordering combineOrdering =
                Ordering.natural().reverse().onResultOf(new Function<Student, Comparable>() {
                    @Nullable
                    @Override
                    public Comparable apply(@Nullable Student input) {
                        return input.getGrade();
                    }
                });
        List<Student> list = Lists.newArrayList();
        list.add(new Student("a", 60));
        list.add(new Student("b", 90));
        list.add(new Student("c", 80));
        list.add(new Student("d", 30));
        Collections.sort(list, combineOrdering);
        System.out.println(list);
    }

输出结果如下：

[Student{name='b', grade=90}, Student{name='c', grade=80}, Student{name='a', grade=60}, Student{name='d', grade=30}]

可以看到，结果确实被很好的排序了

5. Ordering提供的一些实用方法

Ordering.max()//遍历输入集合，取最大值
  @CanIgnoreReturnValue // TODO(kak): Consider removing this
  public <E extends T> E max(Iterator<E> iterator) {
    // let this throw NoSuchElementException as necessary
    E maxSoFar = iterator.next();

    while (iterator.hasNext()) {
      maxSoFar = max(maxSoFar, iterator.next());
    }

    return maxSoFar;
  }

Ordering.min()//遍历输入集合，取最小值
  @CanIgnoreReturnValue // TODO(kak): Consider removing this
  public <E extends T> E min(Iterator<E> iterator) {
    // let this throw NoSuchElementException as necessary
    E minSoFar = iterator.next();

    while (iterator.hasNext()) {
      minSoFar = min(minSoFar, iterator.next());
    }

    return minSoFar;
  }

Ordering.greatestOf()//对比较器做逆序操作，然后取逆序后的比较器的最小的k个值
  public <E extends T> List<E> greatestOf(Iterator<E> iterator, int k) {
    return reverse().leastOf(iterator, k);
  }

Ordering.leastOf
  public <E extends T> List<E> leastOf(Iterator<E> iterator, int k) {
    checkNotNull(iterator);
    checkNonnegative(k, "k");

    if (k == 0 || !iterator.hasNext()) {
      return ImmutableList.of();
    } else if (k >= Integer.MAX_VALUE / 2) {//如果k很大，则直接完全排序然后取头k个结果并返回
      // k is really large; just do a straightforward sorted-copy-and-sublist
      ArrayList<E> list = Lists.newArrayList(iterator);
      Collections.sort(list, this);
      if (list.size() > k) {
        list.subList(k, list.size()).clear();
      }
      list.trimToSize();//压缩数组以释放内存
      return Collections.unmodifiableList(list);
    } else {//用quickselect算法取top k
      TopKSelector<E> selector = TopKSelector.least(k, this);
      selector.offerAll(iterator);
      return selector.topK();
    }
  }

Ordering.isOrdered()//遍历输入集合，检查集合是否有序
  public boolean isOrdered(Iterable<? extends T> iterable) {
    Iterator<? extends T> it = iterable.iterator();
    if (it.hasNext()) {
      T prev = it.next();
      while (it.hasNext()) {
        T next = it.next();
        if (compare(prev, next) > 0) {
          return false;
        }
        prev = next;
      }
    }
    return true;
  }

代码很简单

只有Ordering.leastOf方法有点意思，它会根据传入的k值分情况处理。

如果k < Integer.MAX_VALUE / 2，则调用经典的quickselect算法取TOP K。

如果k >= Integer.MAX_VALUE / 2，则先拷贝传入的集合，然后做全排序，然后取头k个结果，然后再压缩剩余的元素以节省内存。

为什么要这么设计，我不太明白。

我个人的想法是，既然Java的设定是一般集合的大小不能超过Integer.MAX_VALUE，那么如果k >= Integer.MAX_VALUE / 2，直接将比较器反向，然后取TOP（size - k）不就好了吗？