HDU 1542 Atlantis（扫描线）题解

题意：给n个可能相交的矩形，问你不重复的总面积

思路：扫描线，一边扫一边加。

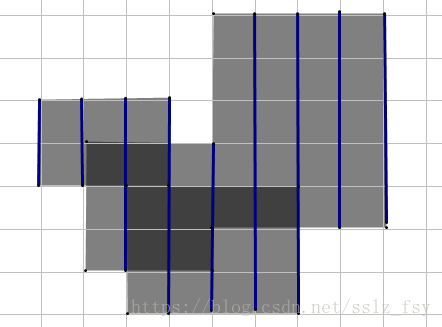
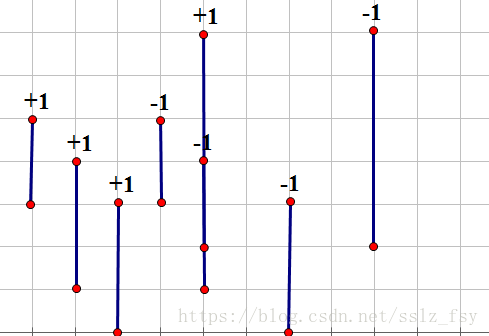
扫描线：图片来源：理解扫描线

假设我们要算以下四个矩形面积，显然中间深色的是重复的。我们按照x的大小，从左往右扫，然后用线段树维护y轴向的长度就可以了。但是，我们不能用点去维护y轴坐标，而是抽象成把点i看成y[i]到y[i+1]这个区间，不然会有错。

代码：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<sstream>
#include<iostream>
#include<algorithm>
typedef long longll;
using namespace std;
const int maxn =  + ;
const int MOD = 1e9 + ;
const int INF = 0x3f3f3f3f;
struct Bian{
    double x, y1, y2;
    int flag;
    bool operator < (const Bian &a) const{
        return x < a.x;
    }
}bian[maxn << ];
double y[maxn << ];    //离散化定位
int n, cnt;
int Find(double x){ //在y中离散化后位置
    int l = , r = cnt, ans = ;
    while(l <= r){
        int m = (l + r) >> ;
        if(fabs(y[m] - x) < 1e-) ans = m;
        if(y[m] > x) r = m - ;
        else l = m + ;
    }
    return ans;
}
int cover[maxn << ]; //y的覆盖次数
double sum[maxn << ];
void pushUp(int l, int r, int rt){
    if(cover[rt] > ) sum[rt] = y[r + ] - y[l];
    //全覆盖了
    else if(l == r) sum[rt] = ;
    //没覆盖的叶子结点
    else sum[rt] = sum[rt << ] + sum[rt <<  | ];
    //部分覆盖
}
void build(int l, int r, int rt){
    if(l == r){
        cover[rt] = sum[rt] = ;
        return;
    }
    int m = (l + r) >> ;
    build(l, m, rt << );
    build(m + , r, rt <<  | );
    cover[rt] = sum[rt] = ;
}
void update(int L, int R, int l, int r, int v, int rt){
    if(L <= l && R >= r){
        cover[rt] += v;
        pushUp(l, r, rt);
        return;
    }
    int m = (l + r) >> ;
    if(L <= m)
        update(L, R, l, m, v, rt << );
    if(R > m)
        update(L, R, m + , r, v, rt <<  | );
    pushUp(l, r, rt);
}
int main(){
    int ca = ;
    while(scanf("%d", &n) && n){
        for(int i = ; i <= n; i++){
            double x1, x2, y1, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            int ll =  * i - , rr =  * i;
            bian[ll].x = x1, bian[ll].y1 = y1, bian[ll].y2 = y2;
            bian[ll].flag = ;
            bian[rr].x = x2, bian[rr].y1 = y1, bian[rr].y2 = y2;
            bian[rr].flag = -;
            y[ll] = y1, y[rr] = y2; //定位用的
        }
        n = n + n;
        sort(bian + , bian + n + );
        sort(y + , y + n + );

        cnt = ;    //unique
        for(int i = ; i <= n; i++){
            if(y[i] != y[i - ]){
                y[++cnt] = y[i];
            }
        }

        double ans = ;
        build(, cnt, );
        for(int i = ; i < n; i++){
            update(Find(bian[i].y1), Find(bian[i].y2) - , , cnt, bian[i].flag, );
            ans += sum[] * (bian[i + ].x - bian[i].x);
        }
        printf("Test case #%d\n", ca++);
        printf("Total explored area: %.2lf\n\n", ans);
    }
    return ;
}