用Python实现的数据结构与算法：基本搜索

一、顺序搜索

顺序搜索 是最简单直观的搜索方法：从列表开头到末尾，逐个比较待搜索项与列表中的项，直到找到目标项（搜索成功）或者 超出搜索范围 （搜索失败）。

根据列表中的项是否按顺序排列，可以将列表分为 无序列表 和 有序列表。对于 无序列表，超出搜索范围 是指越过列表的末尾；对于 有序列表，超过搜索范围 是指进入列表中大于目标项的区域（发生在目标项小于列表末尾项时）或者指越过列表的末尾（发生在目标项大于列表末尾项时）。

1、无序列表

在无序列表中进行顺序搜索的情况如图所示：

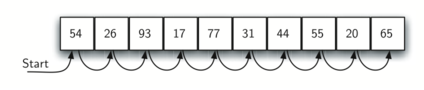
def sequentialSearch(items, target):
    for item in items:
        if item == target:
            return True

    return False

2、有序列表

在有序列表中进行顺序搜索的情况如图所示：

def orderedSequentialSearch(items, target):
    for item in items:
        if item == target:
            return True
        elif item > target:
            break

    return False

二、二分搜索

实际上，上述orderedSequentialSearch算法并没有很好地利用有序列表的特点。

二分搜索 充分利用了有序列表的优势，该算法的思路非常巧妙：在原列表中，将目标项（target）与列表中间项（middle）进行对比，如果target等于middle，则搜索成功；如果target小于middle，则在middle的左半列表中继续搜索；如果target大于middle，则在middle的右半列表中继续搜索。

在有序列表中进行二分搜索的情况如图所示：

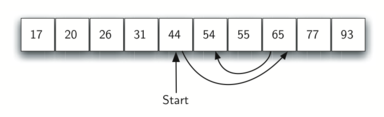
根据实现方式的不同，二分搜索算法可以分为迭代版本和递归版本两种：

1、迭代版本

def iterativeBinarySearch(items, target):
    first = 0
    last = len(items) - 1

    while first <= last:
        middle = (first + last) // 2
        if target == items[middle]:
            return True
        elif target < items[middle]:
            last = middle - 1
        else:
            first = middle + 1

    return False

2、递归版本

def recursiveBinarySearch(items, target):
    if len(items) == 0:
        return False
    else:
        middle = len(items) // 2
        if target == items[middle]:
            return True
        elif target < items[middle]:
            return recursiveBinarySearch(items[:middle], target)
        else:
            return recursiveBinarySearch(items[middle+1:], target)

三、性能比较

上述搜索算法的时间复杂度如下所示：

搜索算法                   时间复杂度
-----------------------------------
sequentialSearch           O(n)
-----------------------------------
orderedSequentialSearch    O(n)
-----------------------------------
iterativeBinarySearch      O(log n)
-----------------------------------
recursiveBinarySearch      O(log n)
-----------------------------------
in                         O(n)

可以看出，二分搜索 的性能要优于 顺序搜索。

值得注意的是，Python的成员操作符 in 的时间复杂度是O(n)，不难猜出，操作符 in 实际采用的是 顺序搜索 算法。

四、算法测试

#!/usr/bin/env python
# -*- coding: utf-8 -*-

def test_print(algorithm, listname, target):
    print('  %d is%s in %s' % (target, '' if algorithm(eval(listname), target) else ' not', listname))

if __name__ == '__main__':
    testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
    orderedlist = sorted(testlist)

    print('sequentialSearch:')
    test_print(sequentialSearch, 'testlist', 3)
    test_print(sequentialSearch, 'testlist', 13)

    print('orderedSequentialSearch:')
    test_print(orderedSequentialSearch, 'orderedlist', 3)
    test_print(orderedSequentialSearch, 'orderedlist', 13)

    print('iterativeBinarySearch:')
    test_print(iterativeBinarySearch, 'orderedlist', 3)
    test_print(iterativeBinarySearch, 'orderedlist', 13)

    print('recursiveBinarySearch:')
    test_print(recursiveBinarySearch, 'orderedlist', 3)
    test_print(recursiveBinarySearch, 'orderedlist', 13)

运行结果：

$ python testbasicsearch.py
sequentialSearch:
  3 is not in testlist
  13 is in testlist
orderedSequentialSearch:
  3 is not in orderedlist
  13 is in orderedlist
iterativeBinarySearch:
  3 is not in orderedlist
  13 is in orderedlist
recursiveBinarySearch:
  3 is not in orderedlist
  13 is in orderedlist