（暂时弃坑）（半成品）ACM数论之旅18---反演定理 第二回 Mobius反演（莫比乌斯反演）（(づ￣3￣)づ天才第一步，雀。。。。）

莫比乌斯反演也是反演定理的一种

既然我们已经学了二项式反演定理

那莫比乌斯反演定理与二项式反演定理一样，不求甚解，只求会用

莫比乌斯反演长下面这个样子(=・ω・=)

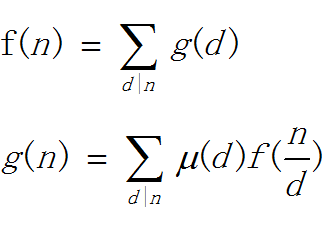
d|n，表示n能够整除d，也就是d是n的所有因子

μ(x)是莫比乌斯函数，它是这样计算的

μ(1) = 1

x = p1 * p2 * p3 ……*pk（x由k个不同的质数组成）则μ(x) = (-1)^k

其他情况，μ (x) = 0

比如

30 = 2 * 3 * 5

μ(30) = (-1)^3

4 = 2 * 2

μ(4) = 0

对于μ(d)函数，它有如下的常见性质：

（1）对任意正整数n有

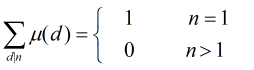
（2）对任意正整数n有

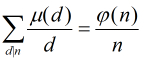
求μ的函数的方法很多

这里提供一种线筛的预处理（复杂度O(n)哟~~~）

 #include<cstdio>
 const int N = 1e6 + ;
 int mu[N], vis[N], prime[N];
 int tot;//用来记录prime的个数
 void init(){
     mu[] = ;
     for(int i = ; i < N; i ++){
         if(!vis[i]){
             prime[tot ++] = i;
             mu[i] = -;
         }
         for(int j = ; j < tot && i * prime[j] < N; j ++){
             vis[i * prime[j]] = ;
             if(i % prime[j]) mu[i * prime[j]] = -mu[i];
             else{
                 mu[i * prime[j]] = ;
                 break;
             }
         }
     }
 }
 int main(){
     init();
 }

上次，有人问我μ为啥不是miu是mu

这。。。当然都可以啦，μ的英文就是mu，miu是读音看你习惯

∑(っ °Д °;)っ为了证明我是对的，我特意百度了希腊字母读音及科学方面应用

大写	小写	英文读音	国际音标	意义
Α	α	alpha	/ˈælfə/	角度，系数，角加速度
Β	β	beta	/'beitə/	磁通系数，角度，系数
Γ	γ	gamma	/'gæmə/	电导系数，角度，比热容比
Δ	δ	delta	/'deltə/	变化量，屈光度，一元二次方程中的判别式
Ε	ε	epsilon	/ep'silon/	对数之基数，介电常数
Ζ	ζ	zeta	/'zi:tə/	系数，方位角，阻抗，相对粘度
Η	η	eta	/'i:tə/	迟滞系数，效率
Θ	θ	theta	/'θi:tə/	温度，角度
Ι	ι ℩	iota	/ai'oute/	微小，一点
Κ	κ	kappa	/kæpə/	介质常数，绝热指数
∧	λ	lambda	/'læmdə/	波长，体积，导热系数
Μ	μ	mu	/mju:/	磁导系数，微，动摩擦系（因）数，流体动力粘度
Ν	ν	nu	/nju:/	磁阻系数，流体运动粘度,光子频率
Ξ	ξ	xi	/ksi/	随机数，（小）区间内的一个未知特定值
Ο	ο	omicron	/oumaik'rən/	高阶无穷小函数
∏	π	pi	/pai/	圆周率，π(n)表示不大于n的质数个数
Ρ	ρ	rho	/rou/	电阻系数，柱坐标和极坐标中的极径，密度
∑	σ ς	sigma	/'sigmə/	总和，表面密度，跨导，正应力
Τ	τ	tau	/tau/	时间常数，切应力
Υ	υ	upsilon	/ju:p'silən/	位移
Φ	φ	phi	/fai/	磁通，角，透镜焦度，热流量
Χ	χ	chi	/kai/	统计学中有卡方(χ^2)分布
Ψ	ψ	psi	/psai/	角速，介质电通量
Ω	ω	omega	/'oumigə/	欧姆，角速度，交流电的电角度

其实莫比乌斯有两种描述

莫比乌斯第一种描述，一般是这种

莫比乌斯第二种描述，这种也可以而且有些题这种更好

来做题吧

hdu 1695

http://acm.hdu.edu.cn/showproblem.php?pid=1695

（这题就是容斥那一章的，我就把下面的题意照搬过来了，还记得题目的就跳过题目吧）

题意:给你5个数a，b，c，d，k

在a~b中选一个x, c~d中选一个y，满足gcd(x,y) = k , 求(x,y) 的对数

a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000

在题目描述的最后一行有一句话，多组里面所有的a和c都是1（这题目不是坑爹吗(╯‵□′)╯︵┻━┻那输入a和c有什么用）

然后题目变成

在1~b中选一个x, 1~d中选一个y，满足gcd(x,y) = k , 求(x,y) 的对数 。。。（无语中。。。）

前面思路一样

先把问题就转化为求1~a区间 和 1~b区间，gcd(x,y) = 1对数的问题

设f(d)为满足gcd(x,y)=d的x,y的对数

我们根据莫比乌斯第二描述来做

那F(1) = f(1) + f(2) + f(3) + ....

F(2) = f(2) + f(4) + f(6) +.....

我们可以看出F(d)就是满足gcd(x,y)为d的倍数的x,y的对数

那F(d)的公式就容易求了

F(d) = (a/d) * (b/d)

（在1~a中，有a/d个数是d的倍数，在1~b中，有b/d个数是d的倍数，这些数不管怎么选择，构成的gcd(x,y)都是d的倍数）

因为

F(1) = f(1) + f(2) + f(3) + ....

所以

f(1) = μ(1)*F(1) + μ(2)*F(2) + μ(3)*F(3) + ...

AC代码：

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 typedef long long LL;
 const int N = 1e6 + ;
 int mu[N], vis[N], prime[N];
 int tot;//用来记录prime的个数
 void init(){
     mu[] = ;
     for(int i = ; i < N; i ++){
         if(!vis[i]){
             prime[tot ++] = i;
             mu[i] = -;
         }
         for(int j = ; j < tot && i * prime[j] < N; j ++){
             vis[i * prime[j]] = ;
             if(i % prime[j]) mu[i * prime[j]] = -mu[i];
             else{
                 mu[i * prime[j]] = ;
                 break;
             }
         }
     }
 }
 LL Mobius(int a, int b){
     LL ret = ;
     for(int i = ; i <= a; i ++){//因为公式中有a/i，所以for到a就可以了
         ret += 1ll * mu[i] * (a / i) * (b / i);
     }
     //我们现在求完了总对数，但是题目要求的类似(5,7)和(7,5)算一种
     //所以接下来我们开始去重
     LL temp = ;
     for(int i = ; i <= a; i ++){
         temp += 1ll * mu[i] * (a / i) * (a / i);
     }
     return ret - temp / ;
     //比如a=5,b=7那么(4,6)这样子的区间不可能有重复的(6,4)
     //所以重复的部分只在1~a中，所以最后减去一半的重复区间就好了
 }
 int main(){
     init();
     int T, a, b, c, d, k;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
         if(k == ){
             printf("Case %d: 0\n", cas);
             continue;
         }
         b /= k; d /= k;
         if(b > d) swap(b, d);
         printf("Case %d: %I64d\n", cas, Mobius(b, d));
     }
 }

/////////////////此处施工中//////////////////

暂时弃坑。。。。

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=94200#overview

峰神挂的莫比乌斯反演章节，有兴趣自己去做做，不会的去百度。。。。