红黑树，TreeMap，插入操作

红黑树

红黑树顾名思义就是节点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。对于一棵有效的红黑树二叉树而言我们必须增加如下规则：

1、每个节点都只能是红色或者黑色

2、根节点是黑色

3、每个叶节点（NIL节点，空节点）是黑色的。

4、如果一个结点是红的，则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。

5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这棵树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。所以红黑树它是复杂而高效的，其检索效率O(log n)。

红黑树的插入操作

如果插入第一个节点，我们直接用树根记录这个节点，并设置为黑色，否则作递归查找插入。

默认插入的节点颜色都是红色，因为插入黑色节点会破坏根路径上的黑色节点总数，但即使如此，也会出现连续红色节点的情况。因此在一般的插入操作之后，出现红黑树约束条件不满足的情况（称为失去平衡）时，就必须要根据当前的红黑树的情况做相应的调整。和AVL树的平衡调整通过旋转操作的实现类似，红黑树的调整操作一般都是通过旋转结合节点的变色操作来完成的。

• 叔父节点是黑色（若是空节点则默认为黑色）

这种情况下通过旋转和变色操作可以使红黑树恢复平衡。但是考虑当前节点n和父节点p的位置又分为四种情况：

A、n是p左子节点，p是g的左子节点。

B、n是p右子节点，p是g的右子节点。

C、n是p左子节点，p是g的右子节点。

D、n是p右子节点，p是g的左子节点。

• 情况A：n是p左子节点，p是g的左子节点。针对该情况可以通过一次右旋转操作，并将p设为黑色，g设为红色完成重新平衡。

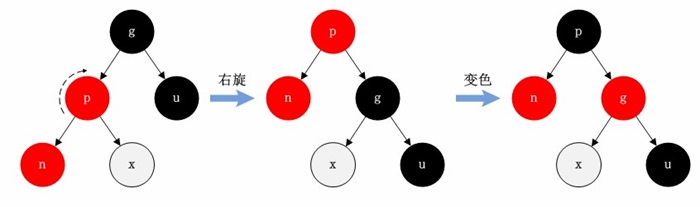
右旋操作的步骤是：将p挂接在g节点原来的位置（如果g原是根节点，需要考虑边界条件），将p的右子树x挂到g的左子节点，再把g挂在p的右子节点上，完成右旋操作。这里将最终旋转结果的子树的根节点作为旋转轴（p节点），也就是说旋转轴在旋转结束后称为新子树的根节点！

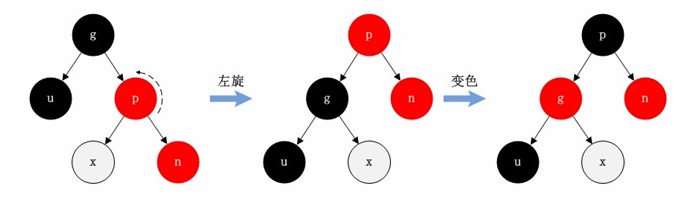
• 情况B则需要使用左单旋操作来解决平衡问题，方法和情况A类似。

• 情况C：n是p左子节点，p是g的右子节点。针对该情况通过一次左旋，一次右旋操作（旋转轴都是n，注意不是p），并将n设为黑色，g设为红色完成重新平衡。

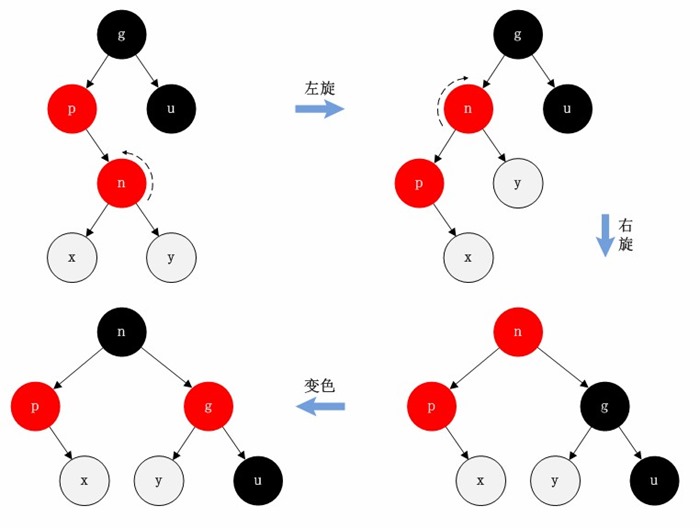
需要注意的是，由于此时新插入的节点是n，它的左右子树x，y都是空节点，但即使如此，旋转操作的结果需要将x，y新的位置设置正确（如果不把p和g的对应分支设置为空节点的话，就会破坏树的结构）。在之后的其他操作中，待旋转的节点n的左右子树可能就不是空节点了。

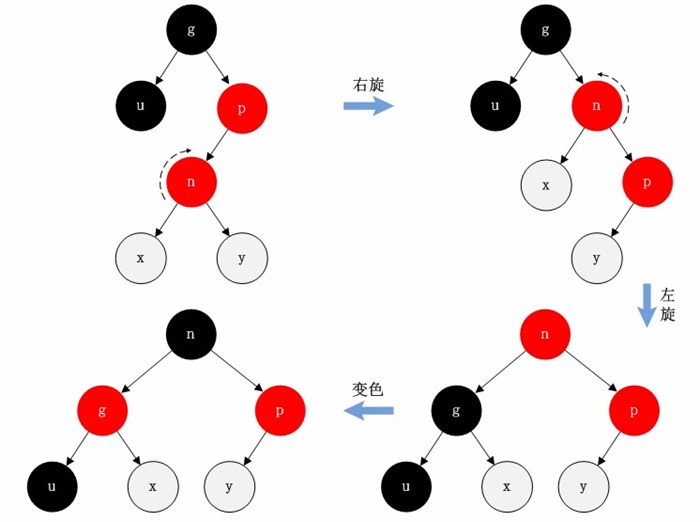
• 情况D则需要使用一次右单旋，一次左单旋操作来解决平衡问题，方法和情况C类似。

• 叔父节点是红色

当叔父节点是红色时，则不能直接通过上述方式处理了（把前边的所有情况的u节点看作红色，会发现节点u和g是红色冲突的）。但是我们可以交换g与p，u节点的颜色完成当前冲突的解决。

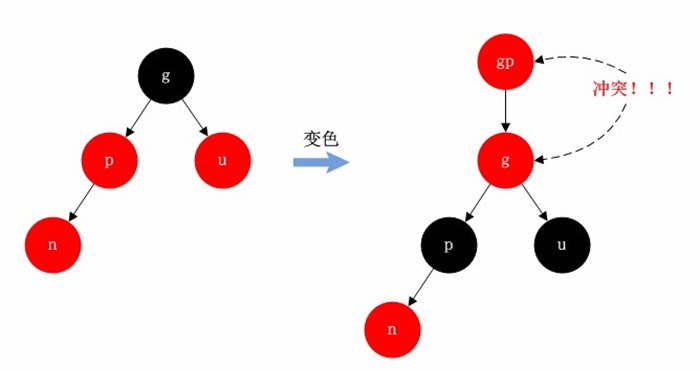
但是仅仅这样做颜色交换是不够的，因为祖父节点g的父节点（记作gp）如果也是红色的话仍然会有冲突（g和gp是连续的红色，违反规则2）。为了解决这样的冲突，我们需要从当前插入点n向根节点root回溯两次。

第一次回溯时处理所有拥有两个红色节点的节点，并按照上图中的方式交换父节点g与子节点p，u的颜色，并暂时忽略gp和p的颜色冲突。如果根节点的两个子节点也是这种情况，则在颜色交换完毕后重新将根节点设置为黑色。

第二次回溯专门处理连续的红色节点冲突。由于经过第一遍的处理，在新插入点n的路径上一定不存在同为红色的兄弟节点了。而仍出现gp和p的红色冲突时，gp的兄弟节点（gu）可以断定为黑色，这样就回归前边讨论的叔父节点为黑色时的情况处理。

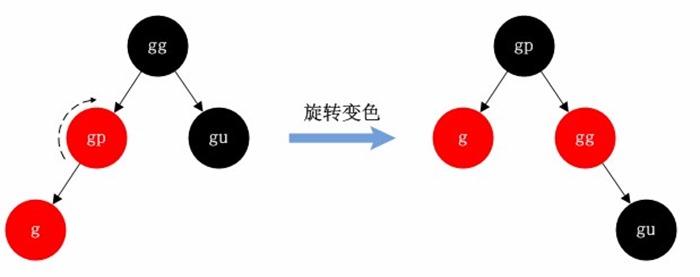
由于发生冲突的两个红色节点位置可能是任意的，因此会出现上述的四种旋转情况。不过我们把靠近叶子的红色节点（g）看作新插入的节点，这样面对A，B情况则把p的父节点gp作为旋转轴，旋转后gp会是新子树的根，而面对C，D情况时把p作为旋转轴即可，旋转后p为新子树的根（因此可以把四种旋转方式封装起来）。

在第二次回溯时，虽然每次遇到红色冲突旋转后都会提升g和gp节点的位置（与根节点的距离减少），但是无论g和gp谁是新子树的根都不会影响新插入节点n到根节点root路径的回溯，而且一旦新子树的根到达根节点（parent指针为空）就可以停止回溯了。

TreeMap数据结构

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

TreeMap继承AbstractMap，实现NavigableMap、Cloneable、Serializable三个接口。其中AbstractMap表明TreeMap为一个Map即支持key-value的集合， NavigableMap则意味着它支持一系列的导航方法，具备针对给定搜索目标返回最接近匹配项的导航方法 。

TreeMap中同时也包含了如下几个重要的属性：

        //比较器，因为TreeMap是有序的，通过comparator接口我们可以对TreeMap的内部排序进行精密的控制
        private final Comparator<? super K> comparator;
        //TreeMap红-黑节点，为TreeMap的内部类
        private transient Entry<K,V> root = null;
        //容器大小
        private transient int size = 0;
        //TreeMap修改次数
        private transient int modCount = 0;
        //红黑树的节点颜色--红色
        private static final boolean RED = false;
        //红黑树的节点颜色--黑色
        private static final boolean BLACK = true;

对于叶子节点Entry是TreeMap的内部类，它有几个重要的属性：

//键
        K key;
        //值
        V value;
        //左孩子
        Entry<K,V> left = null;
        //右孩子
        Entry<K,V> right = null;
        //父亲
        Entry<K,V> parent;
        //颜色
        boolean color = BLACK;

TreeMap put()方法

在TreeMap的put()的实现方法中主要分为两个步骤，第一：构建排序二叉树，第二：平衡二叉树。

对于排序二叉树的创建，其添加节点的过程如下：

1、以根节点为初始节点进行检索。

2、与当前节点进行比对，若新增节点值较大，则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。

3、循环递归2步骤知道检索出合适的叶子节点为止。

4、将新增节点与3步骤中找到的节点进行比对，如果新增节点较大，则添加为右子节点；否则添加为左子节点。

      public V put(K key, V value) {
           //用t表示二叉树的当前节点
            Entry<K,V> t = root;
            //t为null表示一个空树，即TreeMap中没有任何元素，直接插入
            if (t == null) {
                //比较key值，个人觉得这句代码没有任何意义，空树还需要比较、排序？
                compare(key, key); // type (and possibly null) check
                //将新的key-value键值对创建为一个Entry节点，并将该节点赋予给root
                root = new Entry<>(key, value, null);
                //容器的size = 1，表示TreeMap集合中存在一个元素
                size = 1;
                //修改次数 + 1
                modCount++;
                return null;
            }
            int cmp;     //cmp表示key排序的返回结果
            Entry<K,V> parent;   //父节点
            // split comparator and comparable paths
            Comparator<? super K> cpr = comparator;    //指定的排序算法
            //如果cpr不为空，则采用既定的排序算法进行创建TreeMap集合
            if (cpr != null) {
                do {
                    parent = t;      //parent指向上次循环后的t
                    //比较新增节点的key和当前节点key的大小
                    cmp = cpr.compare(key, t.key);
                    //cmp返回值小于0，表示新增节点的key小于当前节点的key，则以当前节点的左子节点作为新的当前节点
                    if (cmp < 0)
                        t = t.left;
                    //cmp返回值大于0，表示新增节点的key大于当前节点的key，则以当前节点的右子节点作为新的当前节点
                    else if (cmp > 0)
                        t = t.right;
                    //cmp返回值等于0，表示两个key值相等，则新值覆盖旧值，并返回新值
                    else
                        return t.setValue(value);
                } while (t != null);
            }
            //如果cpr为空，则采用默认的排序算法进行创建TreeMap集合
            else {
                if (key == null)     //key值为空抛出异常
                    throw new NullPointerException();
                /* 下面处理过程和上面一样 */
                Comparable<? super K> k = (Comparable<? super K>) key;
                do {
                    parent = t;
                    cmp = k.compareTo(t.key);
                    if (cmp < 0)
                        t = t.left;
                    else if (cmp > 0)
                        t = t.right;
                    else
                        return t.setValue(value);
                } while (t != null);
            }
            //将新增节点当做parent的子节点
            Entry<K,V> e = new Entry<>(key, value, parent);
            //如果新增节点的key小于parent的key，则当做左子节点
            if (cmp < 0)
                parent.left = e;
          //如果新增节点的key大于parent的key，则当做右子节点
            else
                parent.right = e;
            /*
             *  上面已经完成了排序二叉树的的构建，将新增节点插入该树中的合适位置
             *  下面fixAfterInsertion()方法就是对这棵树进行调整、平衡，具体过程参考上面的五种情况
             */
            fixAfterInsertion(e);
            //TreeMap元素数量 + 1
            size++;
            //TreeMap容器修改次数 + 1
            modCount++;
            return null;
        }

上面代码中do{}代码块是实现排序二叉树的核心算法，通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可，这样做了其实还没有完成，因为我知道TreeMap的底层实现是红黑树，红黑树是一棵平衡排序二叉树，普通的排序二叉树可能会出现失衡的情况，所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下：

     /**
      * 新增节点后的修复操作
       * x 表示新增节点
       */
     private void fixAfterInsertion(Entry<K,V> x) {
            x.color = RED;    //新增节点的颜色为红色  

            //循环 直到 x不是根节点，且x的父节点不为红色
            while (x != null && x != root && x.parent.color == RED) {
                //如果X的父节点（P）是其父节点的父节点（G）的左节点
                if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
                    //获取X的叔节点(U)
                    Entry<K,V> y = rightOf(parentOf(parentOf(x)));
                    //如果X的叔节点（U） 为红色
                    if (colorOf(y) == RED) {
                        //将X的父节点（P）设置为黑色
                        setColor(parentOf(x), BLACK);
                        //将X的叔节点（U）设置为黑色
                        setColor(y, BLACK);
                        //将X的父节点的父节点（G）设置红色
                        setColor(parentOf(parentOf(x)), RED);
                        x = parentOf(parentOf(x));
                    }
                    //如果X的叔节点（U为黑色）
                    else {
                        //如果X节点为其父节点（P）的右子树，则进行左旋转
                        if (x == rightOf(parentOf(x))) {
                            //将X的父节点作为X
                            x = parentOf(x);
                            //右旋转
                            rotateLeft(x);
                        }  //将X的父节点（P）设置为黑色
                        setColor(parentOf(x), BLACK);
                        //将X的父节点的父节点（G）设置红色
                        setColor(parentOf(parentOf(x)), RED);
                        //以X的父节点的父节点（G）为中心右旋转
                        rotateRight(parentOf(parentOf(x)));
                    }
                }
                //如果X的父节点（P）是其父节点的父节点（G）的右节点
                else {
                    //获取X的叔节点（U）
                    Entry<K,V> y = leftOf(parentOf(parentOf(x)));
                  //如果X的叔节点（U） 为红色
                    if (colorOf(y) == RED) {
                        //将X的父节点（P）设置为黑色
                        setColor(parentOf(x), BLACK);
                        //将X的叔节点（U）设置为黑色
                        setColor(y, BLACK);
                        //将X的父节点的父节点（G）设置红色
                        setColor(parentOf(parentOf(x)), RED);
                        x = parentOf(parentOf(x));
                    }
                  //如果X的叔节点（U为黑色）；这里会存在两种情况
                    else {
                        //如果X节点为其父节点（P）的右子树，则进行左旋转
                        if (x == leftOf(parentOf(x))) {
                            //将X的父节点作为X
                            x = parentOf(x);
                           //右旋转
                            rotateRight(x);
                        }
                        //（情况五）
                        //将X的父节点（P）设置为黑色
                        setColor(parentOf(x), BLACK);
                        //将X的父节点的父节点（G）设置红色
                        setColor(parentOf(parentOf(x)), RED);
                        //以X的父节点的父节点（G）为中心右旋转
                        rotateLeft(parentOf(parentOf(x)));
                    }
                }
            }
            //将根节点G强制设置为黑色
            root.color = BLACK;
        }

• 对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋（rotateRight()）、着色（setColor()）。

• 左旋：rotateLeft()

• 所谓左旋转，就是将新增节点（N）当做其父节点（P），将其父节点P当做新增节点（N）的左子节点。即：G.left ---> N ,N.left ---> P。

private void rotateLeft(Entry<K,V> p) {
        if (p != null) {
            //获取P的右子节点，其实这里就相当于新增节点N（情况四而言）
            Entry<K,V> r = p.right;
            //将R的左子树设置为P的右子树
            p.right = r.left;
            //若R的左子树不为空，则将P设置为R左子树的父亲
            if (r.left != null)
                r.left.parent = p;
            //将P的父亲设置R的父亲
            r.parent = p.parent;
            //如果P的父亲为空，则将R设置为跟节点
            if (p.parent == null)
                root = r;
            //如果P为其父节点（G）的左子树，则将R设置为P父节点(G)左子树
            else if (p.parent.left == p)
                p.parent.left = r;
            //否则R设置为P的父节点（G）的右子树
            else
                p.parent.right = r;
            //将P设置为R的左子树
            r.left = p;
            //将R设置为P的父节点
            p.parent = r;
        }
    }

右旋：rotateRight()

所谓右旋转即，P.right ---> G、G.parent ---> P。

private void rotateRight(Entry<K,V> p) {
        if (p != null) {
            //将L设置为P的左子树
            Entry<K,V> l = p.left;
            //将L的右子树设置为P的左子树
            p.left = l.right;
            //若L的右子树不为空，则将P设置L的右子树的父节点
            if (l.right != null)
                l.right.parent = p;
            //将P的父节点设置为L的父节点
            l.parent = p.parent;
            //如果P的父节点为空，则将L设置根节点
            if (p.parent == null)
                root = l;
            //若P为其父节点的右子树，则将L设置为P的父节点的右子树
            else if (p.parent.right == p)
                p.parent.right = l;
            //否则将L设置为P的父节点的左子树
            else
                p.parent.left = l;
            //将P设置为L的右子树
            l.right = p;
            //将L设置为P的父节点
            p.parent = l;
        }
    }

我是天王盖地虎的分割线

参考：http://blog.csdn.net/chenssy/article/details/26668941