机器学习数学知识中令人费解的notation符号注解
$argmin_xf(x), min(f(x))$
$min(f(x))$的意思是函数$f(x)$的最小值
$argmin$的意思是返回使得表达式取得最小值时对应的输入变量值。例如$argmin_xf(x)$等于当$f(x)$取得最小值时对应的x值。
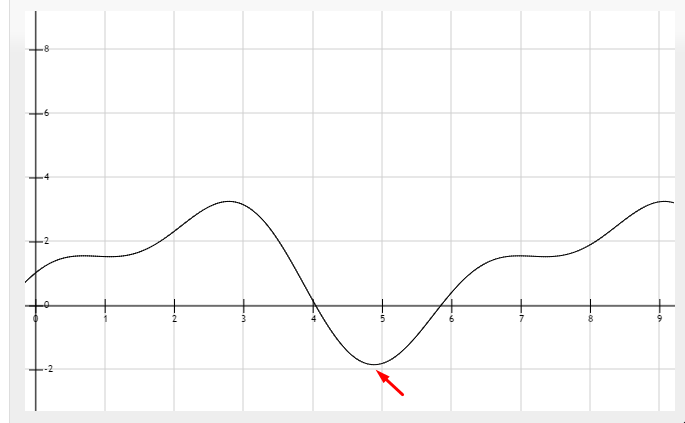
下面的例子中$min(f(x))=-2, argmin_x(f(x))=4.9$
$\textrm{if }k=\arg\min_j\left\Vert\mathbf x_n-\mu_j\right\Vert^2$
完整的符号如下:
$$\pi_nk=\left\{\begin{array}{cl}1 \;\;\; \textrm{if }k=\arg\min_j\left\Vert\mathbf x_n-\mu_j\right\Vert^2\\0 \;\textrm{otherwise}\end{array}\right.$$
这是sk-learn库算法中出现的符号,
$x_n$是已知的,并且依赖于$\pi_nk$,而如果k等于j,这个j使得$\left\Vert\mathbf x_n-\mu_j\right\Vert^2$在所有的$\mu_j$和给定的$x_n$中取得最小值,那么$\pi_nk=1$,否则就为0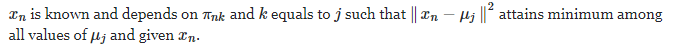

机器学习数学知识中令人费解的notation符号注解的更多相关文章
- HTML5中手势原理分析与数学知识的实践
摘要:在这触控屏的时代,人性化的手势操作已经深入了我们生活的每个部分.现代应用越来越重视与用户的交互及体验,手势是最直接且最为有效的交互方式,一个好的手势交互,能降低用户的使用成本和流程,大大提高了用 ...
- latex:数学式中的省略符号
数学式中有很多省略符号,具体命令符号和用法如下 数学式中的省略符号 \cdots 水平位置与减号等高,例如$-\cdots +$,得到- … + \ddots 对角省略号,例如$A\ddots M$, ...
- Machine Learning Algorithms Study Notes(6)—遗忘的数学知识
机器学习中遗忘的数学知识 最大似然估计( Maximum likelihood ) 最大似然估计,也称为最大概似估计,是一种统计方法,它用来求一个样本集的相关概率密度函数的参数.这个方法最早是遗传学家 ...
- 《DirectX 9.0 3D游戏开发编程基础》必备的数学知识 读书笔记
最近在看游戏导航源码,但是看了几天感觉看不懂.里面全是一些几何运算,以及一些关于3d方面的知识.发现自己缺少3d这方面的知识,正好也想研究一下3d游戏开发的基本原理,于是决定买本书看看了,后来在ope ...
- Rightmost Digit(快速幂+数学知识OR位运算) 分类: 数学 2015-07-03 14:56 4人阅读 评论(0) 收藏
C - Rightmost Digit Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit ...
- codeforces#253 D - Andrey and Problem里的数学知识
这道题是这种,给主人公一堆事件的成功概率,他仅仅想恰好成功一件. 于是,问题来了,他要选择哪些事件去做,才干使他的想法实现的概率最大. 我的第一个想法是枚举,枚举的话我想到用dfs,但是认为太麻烦. ...
- Directx11学习笔记【五】 基本的数学知识----向量篇
本文参考dx11龙书 Chapter1 vector algebra(向量代数) 要想学好游戏编程,扎实的数学知识是尤为重要的,下面将对dx11龙书中有关向量的数学知识做一下总结. 在数学中,几何向量 ...
- 机器学习数学|微积分梯度jensen不等式
机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...
- 机器学习数学|Taylor展开式与拟牛顿
机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 Taylor 展式与拟牛顿 索引 taylor ...
随机推荐
- xampp启动失败 Apache shutdown unexpectedly
我知道是端口被我的虚拟机占用,但是我的虚拟机也要同时打开,所以 我需要修改xampp的端口 1, 2修改二个配置文件 修改httpd.conf 修改httpd-ssl.conf 4,重启xampp
- 《Mysql技术内幕,Innodb存储引擎》——事物
事物 事物中的操作要么都成功要么都不做,这是事物的目的,也是事物模型与文件系统的重要特征之一. 扁平事物(Flat Transactions) 所有操作都处于同一层次,要么都做要么都执行要么都回滚,无 ...
- 简述C和C++的学习历程
总是被问到,如何学习C和C++才不茫然,才不是乱学,想了一下,这里给出一个总的回复. 一家之言,欢迎拍砖哈. 1.可以考虑先学习C. 大多数时候,我们学习语言的目的,不是为了成为一个语言专家,而是希望 ...
- golang-利用反射给结构体赋值
由于想给一个结构体的部分成员赋值,但是有不知道具体名字,故将tag的json名字作为索引,按照json名字来一一赋值 1.通过tag反射//将结构体里的成员按照json名字来赋值 func SetSt ...
- tensorflow 滑动平均使用和恢复
https://www.cnblogs.com/hrlnw/p/8067214.html
- Nodejs学习笔记(七)—Node.js + Express 构建网站简单示例
前言 上一篇学习了一些构建网站会用到的一些知识点:https://www.cnblogs.com/flyingeagle/p/9192936.html 这一篇主要结合前面讲到的知识,去构建一个较为完整 ...
- [codeup] 2044 神奇的口袋
题目描述 有一个神奇的口袋,总的容积是40,用这个口袋可以变出一些物品,这些物品的总体积必须是40.John现在有n个想要得到的物品,每个物品的体积分别是a1,a2--an.John可以从这些物品中选 ...
- npm run build之后生成的dist如何扔到服务器运行(npm run build之后如何本地运行)
运行npm run build之后,会生成一个dist文件夹,里面的目录结构大概是这样的: 生成完的文件我们怎么来运行呢?直接在本地打开inde.html是无法运行的,打包的时候有提示: 构建文件应该 ...
- c#基础学习(0806)之接口学习
首先了解一下什么是接口: 1.接口就是一种规范,协议,约定好遵守某种规范就可以写通用的代码 2.定义了一组具有各种功能的方法(只是一种能力,没有具体实现,像抽象方法一样,“关说不做”) 接口存在的意义 ...
- Linq to xml 操作带命名空间的xml
昨天需要操作用代码操作csproj文件,实现不同vs版本的切换. 在用XElement读取了csproj文件以后怎么也获取不到想要的对象. 反反复复试验了好多次都不得要领:先看下csproj文件的内容 ...
