MP算法和OMP算法及其思想
主要介绍MP(Matching Pursuits)算法和OMP(Orthogonal Matching Pursuit)算法[1],这两个算法尽管在90年代初就提出来了,但作为经典的算法,国内文献(可能有我没有搜索到)都仅描写叙述了算法步骤和简单的应用,并未对其进行详尽的分析,国外的文献还是分析的非常透彻,所以我结合自己的理解,来分析一下写到博客里,算作笔记。
1. 信号的稀疏表示(sparse representation of signals)
给定一个过完备字典矩阵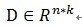 ,当中它的每列表示一种原型信号的原子。给定一个信号y,它能够被表示成这些原子的稀疏线性组合。信号 y 能够被表达为 y = Dx ,或者
,当中它的每列表示一种原型信号的原子。给定一个信号y,它能够被表示成这些原子的稀疏线性组合。信号 y 能够被表达为 y = Dx ,或者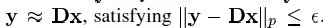 。
。
字典矩阵中所谓过完备性,指的是原子的个数远远大于信号y的长度(其长度非常显然是n),即n<<k。
2.MP算法(匹配追踪算法)
2.1 算法描写叙述
作为对信号进行稀疏分解的方法之中的一个,将信号在完备字典库上进行分解。
假定被表示的信号为y,其长度为n。假定H表示Hilbert空间,在这个空间H里,由一组向量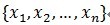 构成字典矩阵D,当中每一个向量能够称为原子(atom),其长度与被表示信号 y 的长度n同样,并且这些向量已作为归一化处理,即|
构成字典矩阵D,当中每一个向量能够称为原子(atom),其长度与被表示信号 y 的长度n同样,并且这些向量已作为归一化处理,即|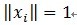 ,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号
,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号
y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,重复迭代,信号y能够由这些原子来线性和,再加上最后的残差值来表示。非常显然,假设残差值在能够忽略的范围内,则信号y就是这些原子的线性组合。假设选择与信号y最匹配的原子?怎样构建稀疏逼近并求残差?怎样进行迭代?我们来具体介绍使用MP进行信号分解的步骤:[1] 计算信号 y 与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号 y 在本次迭代运算中最匹配的。用专业术语来描写叙述:令信号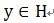 ,从字典矩阵中选择一个最为匹配的原子,满足
,从字典矩阵中选择一个最为匹配的原子,满足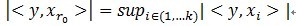 ,r0
,r0
表示一个字典矩阵的列索引。这样,信号 y 就被分解为在最匹配原子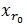 的垂直投影分量和残值两部分,即:
的垂直投影分量和残值两部分,即: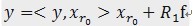 。[2]对残值R1f进行步骤[1]相同的分解,那么第K步能够得到:
。[2]对残值R1f进行步骤[1]相同的分解,那么第K步能够得到:
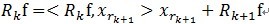 , 当中
, 当中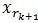 满足
满足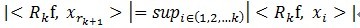 。可见,经过K步分解后,信号 y 被分解为:
。可见,经过K步分解后,信号 y 被分解为: ,当中
,当中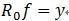 。
。
2.2 继续讨论
(1)为什么要假定在Hilbert空间中?Hilbert空间就是定义了完备的内积空。非常显然,MP中的计算使用向量的内积运算,所以在在Hilbert空间中进行信号分解理所当然了。什么是完备的内积空间?篇幅有限就请自己搜索一下吧。
(2)为什么原子要事先被归一化处理了,即上面的描写叙述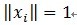 。内积经常使用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比方第一次分解过程中,投影长度就是
。内积经常使用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比方第一次分解过程中,投影长度就是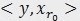 。
。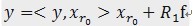 ,三个向量,构成一个三角形,且
,三个向量,构成一个三角形,且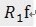 和
和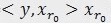 正交(不能说垂直,可是能够想象二维空间这两个矢量是垂直的)。
正交(不能说垂直,可是能够想象二维空间这两个矢量是垂直的)。
(3)MP算法是收敛的,由于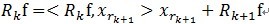 ,
,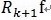 和
和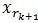 正交,由这两个能够得出
正交,由这两个能够得出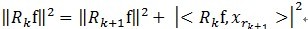 ,得出每个残值比上一次的小,故而收敛。
,得出每个残值比上一次的小,故而收敛。
2.3 MP算法的缺点
如上所述,假设信号(残值)在已选择的原子进行垂直投影是非正交性的,这会使得每次迭代的结果并不少最优的而是次最优的,收敛须要非常多次迭代。举个样例说明一下:在二维空间上,有一个信号 y 被 D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上重复迭代,即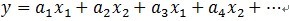 ,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描写叙述[1]可能easy理解:在Hilbert空间H中,
,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描写叙述[1]可能easy理解:在Hilbert空间H中,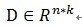 ,
,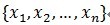 ,定义
,定义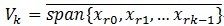 ,就是它是这些向量的张成中的一个,MP构造一种表达形式:
,就是它是这些向量的张成中的一个,MP构造一种表达形式: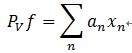 ;这里的Pvf表示
;这里的Pvf表示
f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果能够表演示样例如以下(前面描写叙述时信号为y,这里变成f了,请注意):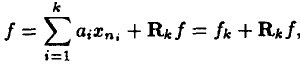
假设  是最优的k项近似值,当且仅当
是最优的k项近似值,当且仅当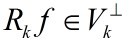 。因为MP仅能保证
。因为MP仅能保证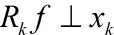 ,所以
,所以 普通情况下是次优的。这是什么意思呢?
普通情况下是次优的。这是什么意思呢? 是k个项的线性表示,这个组合的值作为近似值,仅仅有在第k个残差和
是k个项的线性表示,这个组合的值作为近似值,仅仅有在第k个残差和 正交,才是最优的。假设第k个残值与
正交,才是最优的。假设第k个残值与 正交,意味这个残值与fk的随意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而普通情况下,不能满足这个条件,MP一般仅仅能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。假设第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,非常显然fk就不是最优的,这也就是为什么说MP收敛就须要很多其它次迭代的原因。不是说MP一定得到不到最优解,并且其前面描写叙述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与
正交,意味这个残值与fk的随意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而普通情况下,不能满足这个条件,MP一般仅仅能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。假设第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,非常显然fk就不是最优的,这也就是为什么说MP收敛就须要很多其它次迭代的原因。不是说MP一定得到不到最优解,并且其前面描写叙述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与 正交,方法是有的,这就是以下要谈到的OMP算法。
正交,方法是有的,这就是以下要谈到的OMP算法。
3.OMP算法
3.1 算法描写叙述
OMP算法的改进之处在于:在分解的每一步对所选择的所有原子进行正交化处理,这使得在精度要求同样的情况下,OMP算法的收敛速度更快。
那么在每一步中怎样对所选择的所有原子进行正交化处理呢?在正式描写叙述OMP算法前,先看一点基础思想。
先看一个 k 阶模型,表示信号 f 经过 k 步分解后的情况,似乎非常眼熟,但要注意它与MP算法不同之处,它的残值与前面每一个分量正交,这就是为什么这个算法多了一个正交的原因,MP中仅与近期选出的的那一项正交。
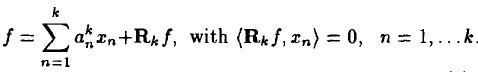 (1)
(1)
k + 1 阶模型例如以下:
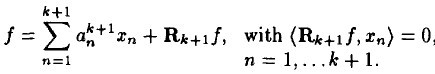 (2)
(2)
应用 k + 1阶模型减去k 阶模型,得到例如以下:
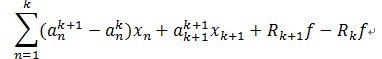 (3)
(3)
我们知道,字典矩阵D的原子是非正交的,引入一个辅助模型,它是表示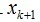 对前k个项
对前k个项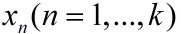 的依赖,描写叙述例如以下:
的依赖,描写叙述例如以下:
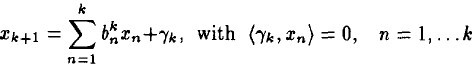 (4)
(4)
和前面描写叙述类似,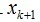 在span(x1, ...xk)之中的一个上的正交投影操作,后面的项是残值。这个关系用数学符号描写叙述:
在span(x1, ...xk)之中的一个上的正交投影操作,后面的项是残值。这个关系用数学符号描写叙述: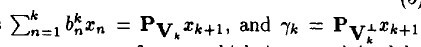
请注意,这里的 a 和 b 的上标表示第 k 步时的取值。
将(4)带入(3)中,有:
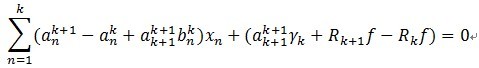 (5)
(5)
假设一下两个式子成立,(5)必定成立。
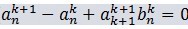 (6)
(6)
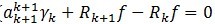 (7)
(7)
令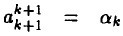 ,有
,有
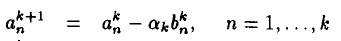
当中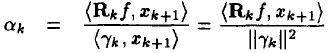 。
。
ak的值是由求法非常easy,通过对(7)左右两边加入�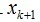 作内积消减得到:
作内积消减得到:
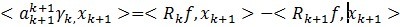
后边的第二项由于它们正交,所以为0,所以能够得出ak的第一部分。对于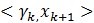 ,在(4)左右两边中与
,在(4)左右两边中与 作内积,能够得到ak的第二部分。
作内积,能够得到ak的第二部分。
对于(4),能够求出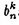 ,求的步骤请參见參考文件的计算细节部分。为什么这里不提,由于后面会介绍更简单的方法来计算。
,求的步骤请參见參考文件的计算细节部分。为什么这里不提,由于后面会介绍更简单的方法来计算。
3.2 收敛性证明
通过(7)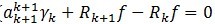 ,因为
,因为 与
与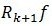 正交,将两个残值移到右边后求二范的平方,并将ak的值代入能够得到:
正交,将两个残值移到右边后求二范的平方,并将ak的值代入能够得到:
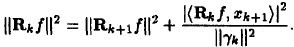
可见每一次残差比上一次残差小,可见是收敛的。
3.3 算法步骤
整个OMP算法的过程例如以下:

因为有了上面的来龙去脉,这个算法就相当好理解了。
到这里还不算完,后来OMP的迭代运算用第二种方法能够计算得知,有位同学的论文[2]描写叙述就很好,我就直接引用进来:


对照中英文描写叙述,本质都是一样,仅仅是有细微的区别。这里顺便贴出网一哥们写的OMP算法的代码,源出处不得而知,共享给大家。

再贴另外一个洋牛paper[3]中关于OMP的描写叙述,之所以引入,是由于它描写叙述的很严谨,可是也有点苦涩难懂,只是有了上面的基础,就easy多了。

它的描写叙述中的Sweep步骤就是寻找与当前残差最大的内积时列在字典矩阵D中的索引,它的这个步骤描写叙述说明为什么要选择内积最大的以及怎样选择。见下图,说的很清晰。
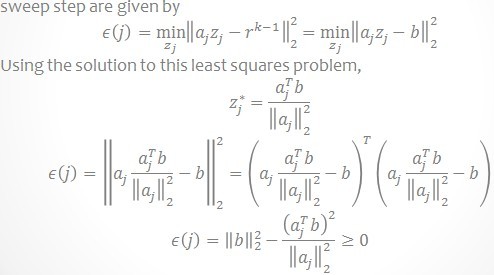
它的算法步骤Update Provisional Solution中求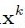 非常easy,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
非常easy,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
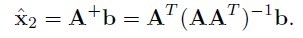
看上去头疼,其有用matlab很easy,看看上面的matlab的代码就明确了。
我们能够看得出来,算法流程清晰明了,还是非常好理解的。这正是OMP算法的魅力,作为工具使用简单,背后却隐藏着非常有趣的思想。
写这篇博客的目的,是由于搜索了一下,MP和OMP没有人非常具体的介绍。文献[1]讲的非常清楚的,大家有兴趣能够找来看看。不要被老板发现我竟然在搜中文文献还写中文博客。
參考文献:
[1] Orthogonal Matching Pursuit:Recursive Function Approximat ion with Applications to Wavelet Decomposition
[2]http://wenku.baidu.com/view/22f3171614791711cc7917e4.html
[3] From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images
MP算法和OMP算法及其思想的更多相关文章
- 最小生成树——Prim算法和Kruskal算法
洛谷P3366 最小生成树板子题 这篇博客介绍两个算法:Prim算法和Kruskal算法,两个算法各有优劣 一般来说当图比较稀疏的时候,Kruskal算法比较快 而当图很密集,Prim算法就大显身手了 ...
- 最小生成树---Prim算法和Kruskal算法
Prim算法 1.概览 普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树.意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (gra ...
- mahout中kmeans算法和Canopy算法实现原理
本文讲一下mahout中kmeans算法和Canopy算法实现原理. 一. Kmeans是一个很经典的聚类算法,我想大家都非常熟悉.虽然算法较为简单,在实际应用中却可以有不错的效果:其算法原理也决定了 ...
- 转载:最小生成树-Prim算法和Kruskal算法
本文摘自:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html 最小生成树-Prim算法和Kruskal算法 Prim算 ...
- 0-1背包的动态规划算法,部分背包的贪心算法和DP算法------算法导论
一.问题描述 0-1背包问题,部分背包问题.分别实现0-1背包的DP算法,部分背包的贪心算法和DP算法. 二.算法原理 (1)0-1背包的DP算法 0-1背包问题:有n件物品和一个容量为W的背包.第i ...
- 最短路径——Dijkstra算法和Floyd算法
Dijkstra算法概述 Dijkstra算法是由荷兰计算机科学家狄克斯特拉(Dijkstra)于1959 年提出的,因此又叫狄克斯特拉算法.是从一个顶点到其余各顶点的最短路径算法,解决的是有向图(无 ...
- FIFO调度算法和LRU算法
一.理论 FIFO:先进先出调度算法 LRU:最近最久未使用调度算法 两者都是缓存调度算法,经常用作内存的页面置换算法. 打一个比方,帮助你理解.你有很多的书,比如说10000本.由于你的书实在太多了 ...
- prim 算法和 kruskal算法
Prim算法 1.概览 普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树.意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (gra ...
- 求最小生成树——Kruskal算法和Prim算法
给定一个带权值的无向图,要求权值之和最小的生成树,常用的算法有Kruskal算法和Prim算法.这两个算法其实都是贪心思想的使用,但又能求出最优解.(代码借鉴http://blog.csdn.net/ ...
随机推荐
- Razor引擎总结
1.显示格式化小数:@(string.Format("{0:0.00}",ViewData["TradeAmount"].ToNullString()))
- python学习之---生成器
通过列表生成式,我们可以直接创建一个列表.但是,受到内存限制,列表容量肯定是有限的.而且,创建一个包含1000万个元素的列表,不仅占用很大的存储空间,如果我们仅仅需要访问前面几个元素,那后面绝大多数元 ...
- 几个RTP的开源实现
玩了两天rtp协议,基本把rtsp/rtcp/rtp/rtmp/srtp/strcp/mms,几个协议的区别和概念弄明白了. 这里记录一下. rtsp:类似用户界面操作,和Http比较类似,提供播放, ...
- mysql日志的查看与开启
mysql的日志类型: 错误日志: log-error 查询日志: log 慢查询日志: log-slow-queries 更新日志: log-update 二进制日志: log-bin 开启错误日志 ...
- 转:三十一、Java图形化界面设计——布局管理器之GridLayout(网格布局)
http://blog.csdn.net/liujun13579/article/details/7772491 网格布局特点: l 使容器中的各组件呈M行×N列的网格状分布. l 网格每列宽度相 ...
- Yii处理流程
Yii的应用程序处理流程 用户访问URL http://www.example.com/blog/index.php?r=site/contact 1.入口脚本被网站服务器执行以处理此请求. 2.一个 ...
- Android Intent.FLAG_NEW_TASK详解,包括其他的标记的一些解释
本文大部分参考自 http://blog.csdn.net/mayingcai1987/article/details/6200909 ,对原文中的讲解FLAG_NEW_TASK地方加了一些自己的观点 ...
- java学习之线程
一.线程总述: 线程是java当中一个重要的内容,如果想说线程的话,那我们应该先来讲一下什么是进程. 进程:那么什么是进程呢,进程从字面上来理解就是,正在进行的程序.就比如说我们在windows当中打 ...
- 《Spark大数据处理:技术、应用与性能优化 》
基本信息 作者: 高彦杰 丛书名:大数据技术丛书 出版社:机械工业出版社 ISBN:9787111483861 上架时间:2014-11-5 出版日期:2014 年11月 开本:16开 页码:255 ...
- [LeetCode#277] Find the Celebrity
Problem: Suppose you are at a party with n people (labeled from 0 to n - 1) and among them, there ma ...
