UR机械臂运动学正逆解方法

最近几个月因为工作接触到了机械臂的项目，突然对机械臂运动方法产生了兴趣，也就是如何控制机械臂的位置和姿态。借用一张网上的图片，应该是ur5的尺寸。我用到的是ur3机械臂，除了尺寸不一样，各关节结构和初始位置和ur5是一样的。

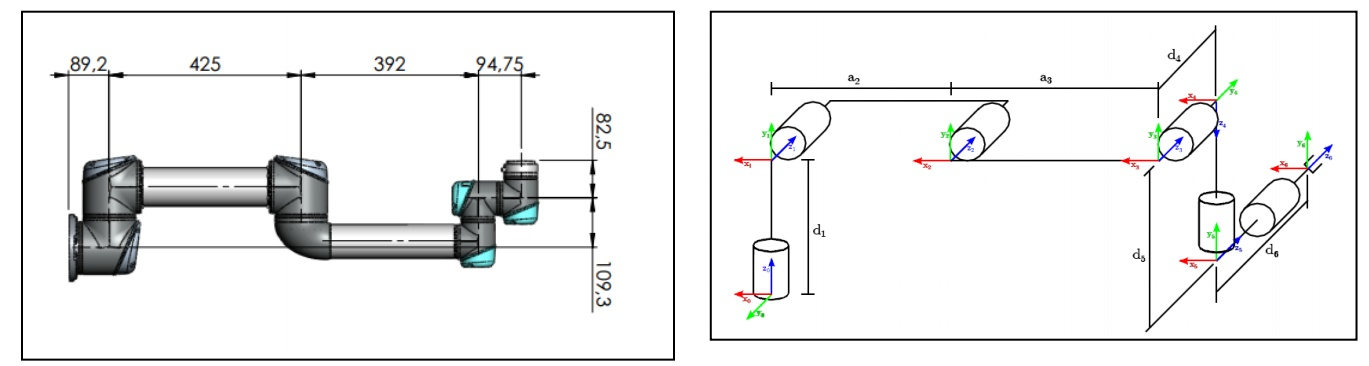
ur机械臂是六自由度机械臂，由D-H参数法确定它的运动学模型，连杆坐标系的建立如上图所示。我当时在这个地方的理解上走了不少弯路，后来找个一个视频，我觉得讲解地比较容易理解，可以参考一下Denavit-Hartenberg参数视频详解。ur机械臂DH参数表如下，

转动关节θ_i是关节变量，连杆偏移d_i是常数。

关节编号	α（绕x轴）	a（沿x轴）	θ（绕z轴）	d（沿z轴）
1	α1=90	0	θ1	d1=89.2
2	0	a2=-425	θ2	0
3	0	a3=-392	θ3	0
4	α4=90	0	θ4	d4=109.3
5	α5=-90	0	θ5	d5=94.75
6	0	0	θ6	d6=82.5

由此可以建立坐标系i在坐标系i-1的齐次变换矩阵，注意每次不管平移还是旋转是相对于当前的运动坐标系变换，矩阵右乘

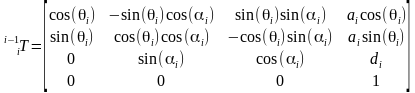
那么把DH参数代入就可以得到所有相邻坐标系的变换矩阵

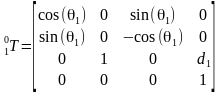
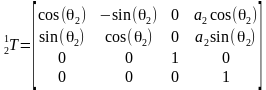
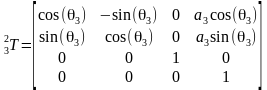
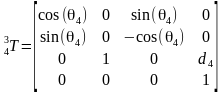
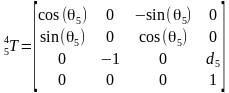
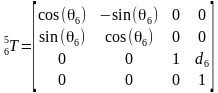
所以末端坐标系6到基座固定坐标系0的变换矩阵。那么求正解就很简单了，只要输入六个关节角度θ_i，就得到末端坐标在基坐标系的变换矩阵T。ur机械臂的视教板上末端点的坐标是用六个值[x, y, z, rx, ry, rz]表示的。前三个值[x, y, z]是三维笛卡尔坐标，表示空间位置，后三个值[rx, ry, rz]是坐标旋转向量，表示空间姿态。我们得到的变换矩阵T怎么变成六值坐标[x, y, z, rx, ry, rz]呢？设

T的左上角的3x3矩阵是旋转矩阵，旋转矩阵和旋转向量之间可以通过罗德里格斯（Rodrigues）变换进行转换。opencv里有相应的函数调用。算法也比较简单，不用opencv的函数自己写代码也不难。T的右上角3x1就是空间位置[x, y, z]。这样有变换矩阵T得到六值坐标，完成了正解。

逆解相对要复杂一些，由末端的空间位置和姿态，计算可能的关节角度。逆解的方法有解析法，迭代法和几何法。其中解析法用数学推导，可以得到全部根，但是计算复杂。有的机械臂可以得到无穷解，比如7轴机械臂。而ur的6轴机械臂是有有限解的。这里推导一下ur的逆解。

首先计算求变换矩阵T过程其中的一些中间矩阵。

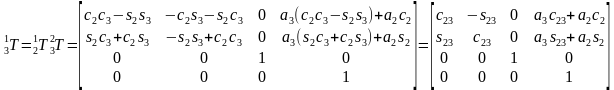，其中c₂₃=cos(θ₂+θ₃)，s₂₃=sin(θ₂+θ₃)。

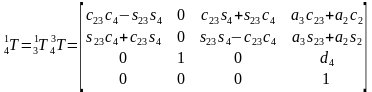
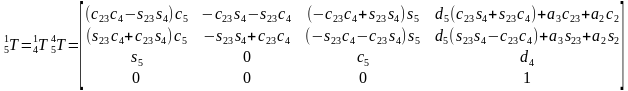
由得到。计算

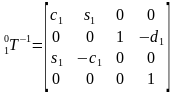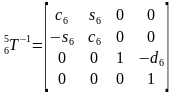，，得到

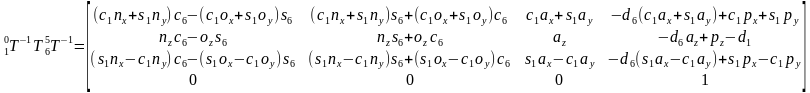
等式两边矩阵的行列应该分别相等，由第三行第四列得到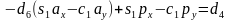，可解得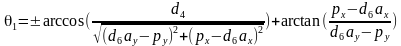，有两个解。这里注意写程序的时候，求解这里的反正切是用atan2()这类的函数，返回之在(-π,+π]。而反余弦的返回值在[0,π]，从而保证在2π范围两个解是不同的。

由第三行第三列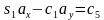得，可解得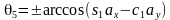，两个解。由第三行第二列得到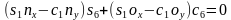，可解得。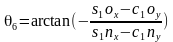

接着由

，

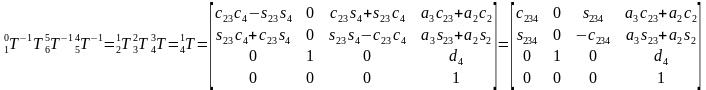计算

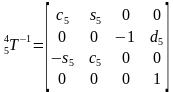，得出等式左边等于

。

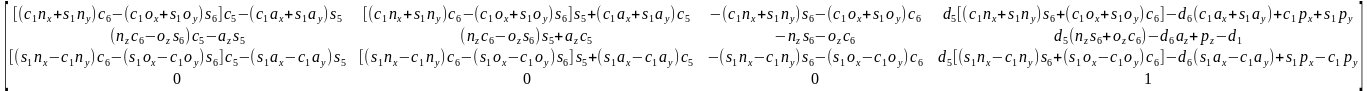由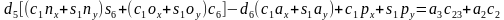，两边平方，令，。

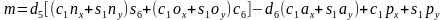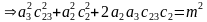同样由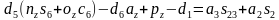，令，。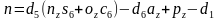

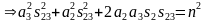两式相加得到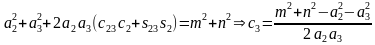，则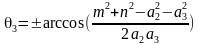，有两个解。

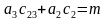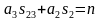把θ₃带入和，得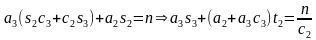，，其中t₂=tanθ₂。两式消去c₂，得到。

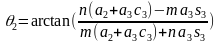最后得到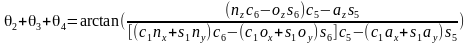，从而得到θ₄。

p { margin-bottom: 0.1in; line-height: 120% }
a:link { }

综合有两个解的情况，ur机械臂逆解总共由2x2x2=8组解。

按照上面的算法，用python写了两个程序，一个正解一个逆解验证一下。工作手边是ur3的机械臂，上面的图和表都是ur5的，换成ur3的参数。正解算出来都没有问题，可以和实际机械臂的空间位姿对应。可是逆解算出来8组值，好像只有四组值是对的。一直还没理解到底是怎么回事，仔细检查了算法和程序好像都没有错阿，不知道是哪里出了问题。网上也没有找到答案，如果哪位大神知道，望不吝赐教！