Floyd 算法求多源最短路径

Floyd算法:

　　Floyd算法用来找出每对顶点之间的最短距离,它对图的要求是,既可以是无向图也可以是有向图,边权可以为负,但是不能存在负环(可根据最小环的正负来判定).

基本算法:

　　Floyd算法基于动态规划的思想,以 u 到 v 的最短路径至少经过前 k 个点为转移状态进行计算,通过 k 的增加达到寻找最短路径的目的.当 k 增加 1 时,最短路径要么不边,如果改变,必经过第 k 各点,也就是说当起点 u 到第 k 个点的最短距离加上第 k 个点到终点 v 的最短路径小于不经过第 k 个节点的最优最短路经长度的时候更新 u 到 v 的最短距离. 当 k = n 时, u 到 v 的最短路径就确定了.

伪代码:

　　图的存储用邻接矩阵 gra[][] 来记录,如果 u 与 v 之间没有边直接相连,则 gra[u][v] = INF; dist[][] 记录最终的最短路. pre[i][j] 存储 i 到 j 路径中 i 的后一个节点.

　　1): 初始化:将 gra 中的数据复制到 dist 中作为每对顶点间的最短路的初值, pre[i][j] = j;

　　2): k 从 1 到 n 循环 n 次, 每次循环中枚举图中不同的两点 u, v, 如果 dist[u][v] > dist[u][k] + dist[k][v], 则更新 dist[u][v] = dist[u][k] + dist[k][v], 更新 pre[u][v] = pre[u][k].

　　3): 最后 dist[u][v] 数组中存储的就是 u 到 v 的最短距离, u 到 v 的路径, 则可以按照顺序查找就好了.

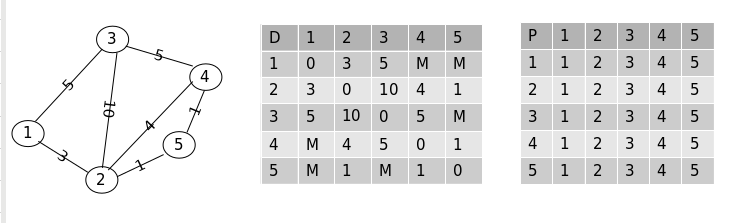
以图为例:

有一个如下的无向图, “D”数组存储最短路值, “P” 数组存储最短路径:

假设现在每对顶点之间的路径只允许经过点 “1” , 则更新后的每对顶点之间的距离:

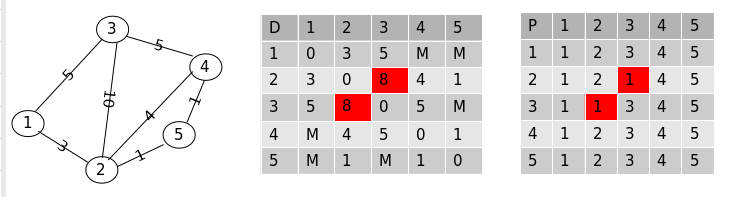
这里看到点 “2” 到点 “3” 的距离经过点 “1” 得到了更新,同时更新了用于记录路径的 P 数组.

第二步,允许每对顶点之间的最短路径经过点 “1” 和点 “2”,则更新后的数组为:

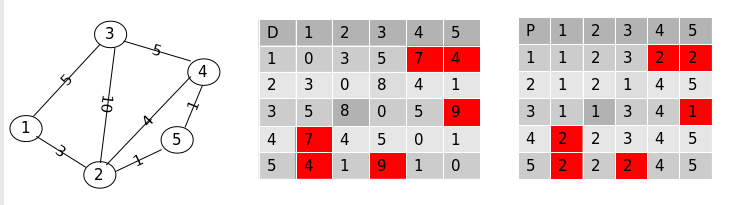
可以看到得到更新的路径为:

1 ---> 4, 经过点 “2” 得到更新

1 ---> 5, 经过点 “2” 得到更新

3 ---> 5. 经过点 “1 --- > 2” 得到更新

第三步: 允许经过点 “1”, “2” 和点 “3” 则更新后的数组为:

这则说明,上一步的最短路径不需要更新.

第四步, 允许经过点 “1”, “2” , “3” 和点 “4” 则更新后的数组为:

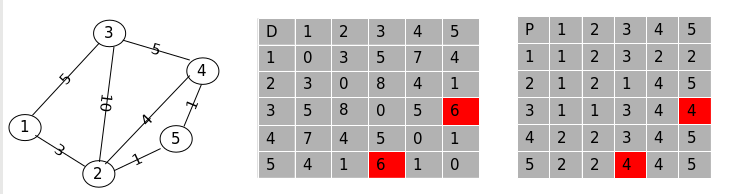
可以看到 3 ---> 5 的路径经过点 “4” 得到了更新(原先是 3 ---> 1 ---> 2 ---> 5, w = 9)

第五步, 允许任意两点之间的最短路径可以经过全部点,则更新后的数组为:

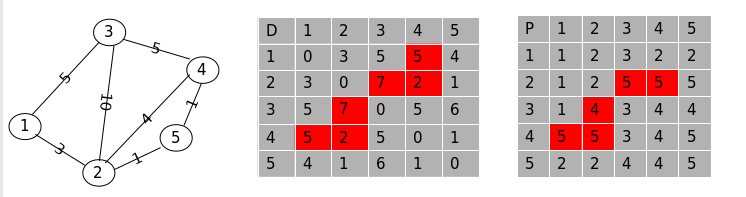
这次得到更新的路径为:

1 ---> 4 的路径. 更新为 “1 ---> 2 ---> 5 ---> 4, w = 5” (原路径为 1 ---> 2 ---> 4, w = 7)

2 ---> 3 的路径. 更新为 “2 ---> 5 ---> 4 ---> 3, w = 7” (原路经为 2 ---> 1 ---> 3, w = 8)

2 ---> 4 的路径. 更新为 “2 --> 5 --> 4, w = 2” (原路径为 2 ---> 4, w = 4)

无向图反之亦然.

至此最短路径就寻找完毕. dist[i][j] 数组里面保存的就是 i 到 j 的最短距离.如果要查寻路径, 则按照查数组 pre 就好.比如查询 “2” 到 “3” 的路径:

则寻找     pre[2][3] = 5,  2 ---> 5

继续寻找  pre[5][3] = 4,  2 ---> 5 ---> 4

继续寻找  pre[4][3] = 3, 2 ---> 5 ---> 4 ---> 3

由于此时 i = j = 3, 则 “2” 到 “3” 的最短路径已找到为: 2 ---> 5 ---> 4 ---> 3

 #include <bits/stdc++.h>

 typedef long long LL;
 const int MAXN = ;
 const int INF = 0x3f3f3f3f;
 using namespace std;

 int pre[MAXN + ][MAXN + ], dist[MAXN + ][MAXN + ]; //pre 储存路径; dist 存储最短距离
 void floyd(int n, int gra[][MAXN + ]) {
     for(int i = ; i <= n; i++) for(int j = ; j <= n; j++) dist[i][j] = gra[i][j], pre[i][j] = j;  //初始化
     for(int k = ; k <= n; k++) {   //尝试经过 k 个点对每对顶点之间的距离进行更新
         for(int i = ; i <= n; i++) {
             for(int j = ; j <= n; j++) {
                 if(dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
                     dist[i][j] = dist[i][k] + dist[k][j];
                     pre[i][j] = pre[i][k];
                 }
             }
         }
     }
 }

 int pfpath(int u, int v) { //打印最短路径
     while(u != v) {
         cout << u  << " ";
         u = pre[u][v];
     }
     cout << u << endl;
 }

 int gra[MAXN + ][MAXN + ];
 int main() {
     int n, m;
     while(cin >> n >> m){ // n 个点,  m 条边
         for(int i = ; i <= n; i++) for(int j = -; j <= n; j++){
             gra[i][j] = (i == j ?  : INF);
         }
         for(int i = ; i < m; i++) {
             int u, v, w; cin >> u >> v >> w;
             gra[u][v] = gra[v][u] = w;  //无向图
         }
         floyd(n, gra);
     }
     return ;
 }