洛谷 [P3973] 线性代数

最大权闭合子图，神题

这不是线性代数，这是网络流。

我们看见这是一堆矩阵的运算，而且最后变成了一个数，那么我们就想到，把这个矩阵乘法的过程用具体的数字推出来

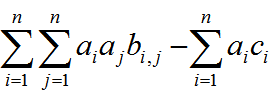
我们发现，a是一个01矩阵，然后其实就可以化成这么一个问题：

有n个东西，选了i,j两件东西能得到b[i,j]的价值，然而选i需要c[i]的花费，选j需要c[j]的花费……

这是一个经典的最小割模型，最大权闭合子图，详见胡伯涛论文。

建立S,T。

S连(i,j)边，边权为b[i,j]，(i,j)连i、连j边，边权均为∞，i向T连边，边权为c[i]。

然后求最小割，最后答案就是

sum(b[i][j])-最小割答案 (i∈[1..n],j∈[1..n])

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <bitset>
#include <queue>
#define inf 0x3f3f3f3f
using namespace std;
const int MAXN = 300005;
int n, b[505][505], c[505], s, t, head[MAXN], nume, MaxFlow, ans, dep[MAXN], cur[MAXN];
int init() {
	int rv = 0, fh = 1;
	char c = getchar();
	while(c < '0' || c > '9'){
		if(c == '-') fh = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		rv =  (rv<<1) + (rv<<3) + c -'0';
		c = getchar();
	}
	return fh * rv;
}
struct edge{
	int to, nxt, flow, cap;
}e[MAXN<<4];
void adde(int from, int to, int cap){
	e[++nume].to = to;
	e[nume].nxt = head[from];
	e[nume].cap = cap;
	head[from] = nume;
}
queue <int> q;
bool bfs(){
	q.push(s);
	memset(dep,0,sizeof(dep));
	dep[s]=1;
	while(!q.empty()){
		int u = q.front();q.pop();
		for(int i = head[u] ; i ; i = e[i].nxt){
			int v = e[i].to;
			if(!dep[v]&&e[i].flow < e[i].cap){
				dep[v] = dep[u] + 1;
				q.push(v);
			}
		}
	}
	return dep[t];
}
int dfs(int u, int flow) {
	if(u == t) return flow;
	int tot = 0;
	for(int &i = cur[u] ; i&&tot < flow ; i = e[i].nxt) {
		int v = e[i].to;
		if(dep[v] == dep[u] + 1&&e[i].flow < e[i].cap) {
			if(int t = dfs(v, min(e[i].cap - e[i].flow, flow - tot))) {
				tot += t;
				e[i].flow += t;
				e[((i-1) ^ 1 ) + 1].flow -= t;
			}
		}
	}
	return tot;
}
void dinic(){
	while(bfs()) {
		memcpy(cur,head,t*4+4);
		MaxFlow+=dfs(s, 0x3f3f3f3f);
	}
}
int main() {
	freopen("in.txt", "r", stdin);
	n=init();
	for(int i = 1 ; i <= n ; i++) {
		for(int j = 1; j <= n; j++) {
			b[i][j] = init();
			ans += b[i][j];
		}
	}
	for(int i = 1;i <= n;i++){
		c[i]=init();
	}
	s=0;t=n*n+n+1;
	for(int i = 1;i <= n ;i++){
		for(int j = 1;j <= n;j++){
			adde(s,i*n+j-n,b[i][j]);
			adde(i*n+j-n,s,0);
		}
	}
	for(int i = 1;i <= n;i++) {
		adde(n*n+i, t, c[i]);
		adde(t, n*n+i, 0);
	}
	int kkk=n*n;
	for(int i = 1;i <= n ;i++) {
		int ttt=i*n-n;
		for(int  j=1 ;j <=n ;j++) {
			adde(ttt+j,kkk+i,inf);
			adde(kkk+i,ttt+j,0);
			adde(ttt+j,kkk+j,inf);
			adde(kkk+j,ttt+j,0);
		}
	}
	dinic();
	cout<<ans-MaxFlow<<endl;
	fclose(stdin);
	return 0;
}