[codeforces 901E] Cyclic Cipher 循环卷积-Bluestein's Algorithm

题目大意：

　　传送门

　　给两个数列${B_i}、{C_i}$，长度均为$n$，且${B_i}$循环移位线性无关，即不存在一组系数${X_i}$使得对于所有的$k$均有$\sum_{i=0}^{n-1} X_i  B_{k-i \mod n} =0$。

　　已知$C$是由$B$与$A$构造得到：

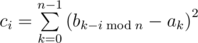　 　(搬原图)。

　　求所有合法的$A$序列。

题解：

　　首先把式子稍加化简会得到:

　　显然是个差分式，然后就会得到以下两种结果（以下$B_{i}$均为$B_{i\mod n}$）：

　　　　

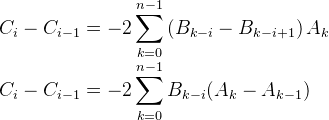
　　问题是，这两个式子都是对的吗？

　　显然不是。

　　我们考虑题目中说的${B_i}$为循环移位线性无关，但是$\Delta B_i=B_{i+1}-B_{i}$构成的${\Delta B_{i}}$我们是不知道它是否是线性无关的，如果是线性无关，那么它是正确的，反之，我们会知道必然存在一组${X_i}$使得若${A}$有解，则有无穷解，但是回带是错误的。

　　但是二式我们如果可以求解可知$\Delta A_i=A_{i+1}-A{i}$是有唯一解的，然后考虑回带求$A_0$我们就可以得到最多两个解。

　　所以本题就变成了求：

　　 

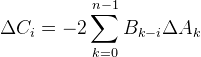
　　设$B'_i=B_{-i}$，即：

　　  

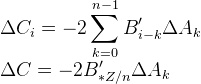
　　即，问题变为求出$\Delta C$的点值然后除去$B'_{*Z/n}$的点值再除去$-2$我们再由$\Delta A$的点值求出其系数即可。

　　当然，我们可以知道$\Delta A$的系数小于$2e3$，所以我们防止卡精使用$NTT$。

　　由于并不知道$B'_{*Z/n}$的长度，所以不能裸上，需要使用Bluestein's Algorithm。

　　这个东西网上几乎没有讲解，好像毛爷爷的《再探》里面有说？

　　具体就是：

　　

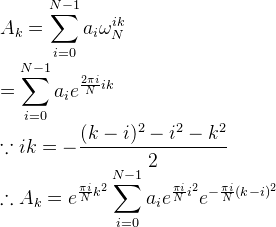
　　这样就可以使用一次卷积来求$B'$的点值了。（$NTT$并不能直接拆成上面的形式，因为数论变换是没法消去下面除的那个2）

　　所以将$ik$变为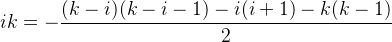然后拆解即可。

代码：

 #include "bits/stdc++.h"
 
 typedef long long ll;
 
 inline int read() {
     int s=,k=;char ch=getchar();
     while (ch<''|ch>'') ch=='-'?k=-:,ch=getchar();
     while (ch>&ch<='') s=s*+(ch^),ch=getchar();
     return s*k;
 }
 
 const int N=6e5+;
 
 ll mod,g,w[][N],W[][N];
 
 inline ll Mult ( ll a,ll b ) {
     return ( a*b - (ll)( (long double) a*b/mod )*mod + mod )% mod;
 }
 
 inline ll powmod ( ll a, ll b ) {
     ll ret=;
     while (b) {
         if (b&) ret=Mult ( ret, a );
         b>>=,a=Mult ( a, a);
     }return ret;
 }
 
 inline ll gcd  ( ll a,ll b ) { return b?gcd(b,a%b) : a; }
 
 int n,m;
 
 inline void Get_mod () {
     for (m=; (m<=*n) ;m<<= );
     ll lcm =1ll* n*m /gcd (n,m);
     mod = lcm + ;
     while ( mod < 1e5 )  mod += lcm;
     while () {
         int flag=true;
         for (int i=;1ll*i*i<=mod;++i) if (mod%i==) {flag=false;break;}
         if (flag) break;
         mod+=lcm;
     }
     for (g=;;++g) {
         int flag=true;
         for (int i=;1ll*i*i<=mod;++i) if ((mod-)%i==){
             if (powmod(g,i)==) {flag=false;break;}
             if (powmod(g,(mod-)/i)==) {flag=false;break;}
         }
         if (flag) break;
     }
 }
 
 inline void Get_wn(){
     ll w0=powmod(g,(mod-)/m);
     w[][]=w[][]=;
     int i;
     for (i=;i<m;++i) w[][i]=Mult(w[][i-],w0);
     for (i=;i<m;++i) w[][i]=w[][m-i];
     w0=powmod(g,(mod-)/n);
     W[][]=W[][]=;
     for (i=;i<n;++i) W[][i]=Mult(W[][i-],w0);
     for (i=;i<n;++i) W[][i]=W[][n-i];
 }
 
 inline void NTT(ll *a,int n,int f) {
     register int i,j,k,l,t;
     for (i=j=;i^n;++i) {
         if (i>j) std::swap(a[i],a[j]);
         for (k=n>>;(j^=k)<k;k>>=);
     }
     for (i=;i<n;i<<=)
         for (j=,t=n/(i<<);j<n;j+=i<<)
             for (k=l=;k<i;++k , l+=t ) {
                 ll x=a[j+k],y=Mult(a[i+j+k],w[f][l]);
                 a[j+k]=x+y;
                 a[i+j+k]=x-y;
                 if (a[j+k]>=mod) a[j+k]-=mod;
                 if (a[i+j+k]<) a[i+j+k]+=mod;
             }
     if (f ) {
         ll rev=powmod ( n,mod- );
         for (i=;i<n;++i) a[i]=Mult(a[i],rev);
     }
 }
 
 ll Y[N];
 
 inline void pre_Bluestein(int f) {
     int i;
     for (i=;i<*n;++i) Y[*n--i]=W[f][1ll*i*(i-)/%n];
     for (i=*n;i<m;++i) Y[i]=;
     NTT(Y,m,);
 }
 
 inline void Bluestein(ll *a,int f){
     static ll X[N];
     register int i;
     for (i=;i<n;++i) X[i]=Mult(a[i],W[f][ (n-1ll*i*(i-)/%n)%n ]);
     for (i=n;i<m;++i) X[i]=;
     NTT(X,m,);
     for (i=;i<m;++i) X[i]=Mult(X[i],Y[i]);
     NTT(X,m,);
     for (i=;i<n;++i)
         a[i]=Mult (X[*n--i],W[f][(n-1ll*i*(i-)/%n)%n ]);
     if (f)  {
         ll rev=powmod(n,mod-);
         for (i=;i<n;++i) a[i]=Mult(a[i],rev);
     }
 }
 
 int b[N],c[N];
 ll rev_b[N],delta_c[N],delta_a[N],a[N];
 
 int main() {
     //freopen(".in","r",stdin);
     n = read();
     register int i;
     for (i=;i<n;++i) b[i]=read();
     for (i=;i<n;++i) c[i]=read();
     Get_mod();
     Get_wn();
     for (i=;i<n;++i) rev_b[i]=b[i];
     std::reverse(rev_b+,rev_b+n);
     ll inv_2=powmod(mod-,mod-);
     for (i=;i<n;++i) delta_c[i]=Mult ( ( c[(i+)%n]-c[i] + mod )%mod , inv_2 );
     pre_Bluestein();
     Bluestein(rev_b,);
     Bluestein(delta_c,);
     for (i=;i<n;++i) delta_a[i]=Mult ( delta_c[i] , powmod (rev_b[i],mod-) );
     pre_Bluestein();
     Bluestein(delta_a,);
     for (i=;i<n;++i) {
         ll v=(delta_a[i]<mod-delta_a[i])?delta_a[i]:delta_a[i]-mod;
         if (abs(v)>) return puts(""),;
         a[i]=v;
     }
     ll _c=-c[],_a=,_b=,sum=;
     for (i=;i<n;++i) {
         ++_a;
         _b+=*(sum-b[i]);
         _c+=(sum-b[i])*(sum-b[i]);
         sum+=a[i];
     }
     if (sum!=) {
         puts("");
         return ;
     }
     std::set<ll> ans;
     if (_b*_b-*_a*_c>=){
         ll s=ll(sqrt(_b*_b-*_a*_c) + 0.5);
         if (s*s!=_b*_b-*_a*_c) return puts(""),;
         if ((-_b+s)%(*_a)==) ans.insert((-_b+s)/(*_a));
         if ((-_b-s)%(*_a)==) ans.insert((-_b-s)/(*_a));
     }
     std::set<ll>::iterator it;
     printf("%d\n",ans.size());
     for (it=ans.begin();it!=ans.end();++it) {
         ll now=*it;
         for (i=;i<n;++i){
             printf("%lld ",now);
             now+=a[i];
         }
         puts("");
     }
 }

codeforces901E