多项式A除以B

这个问题我是在PAT大区赛题里遇见的。题目如下：

多项式A除以B（25 分）

这仍然是一道关于A/B的题，只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R，其中R的阶数必须小于B的阶数。

输入格式：

输入分两行，每行给出一个非零多项式，先给出A，再给出B。每行的格式如下：

N e[1] c[1] ... e[N] c[N]

其中N是该多项式非零项的个数，e[i]是第i个非零项的指数，c[i]是第i个非零项的系数。各项按照指数递减的顺序给出，保证所有指数是各不相同的非负整数，所有系数是非零整数，所有整数在整型范围内。

输出格式：

分两行先后输出商和余，输出格式与输入格式相同，输出的系数保留小数点后1位。同行数字间以1个空格分隔，行首尾不得有多余空格。注意：零多项式是一个特殊多项式，对应输出为0 0 0.0。但非零多项式不能输出零系数（包括舍入后为0.0）的项。在样例中，余多项式其实有常数项-1/27，但因其舍入后为0.0，故不输出。

输入样例：

4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1

输出样例：

3 2 0.3 1 0.2 0 -1.0
1 1 -3.1

题目的意思很明确，就是要求 anxn+an-1xn-1+an-2xn-2+。。。+a1x1+a0x0 除以amxm+am-1xm-1+am-2xm-2+。。。+a1x1+a0x0 的商和余数。这可以类比多项式除法进行。
这题的样例数据可表示为：x4-3x2-x-1 除以 3x2-2x+1 求其的商和余数。

手工计算步骤就是下图所示：
依次乘一个(1/3)x2,(2/9)x,(-26/27),很明显就是想办法消掉最高次项，知道所剩的余项最高次小于除数的最高次。

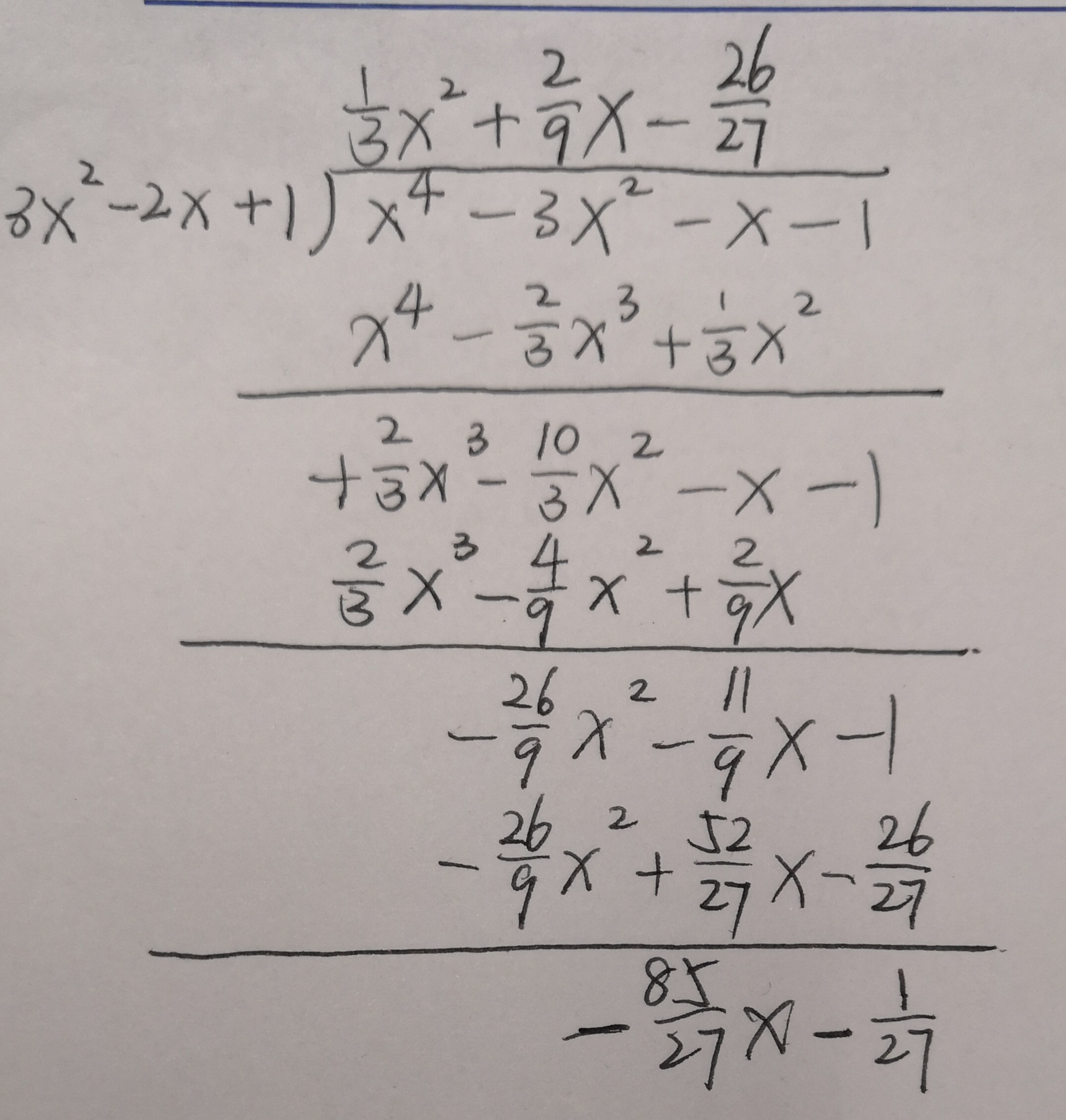
分数化简后就为答案。（上方为商，下方为余数）。

算法核心部分上面已经讲了，接下来讲一下数据结构的设置。

因为每一项都是指数、系数这两个变量，所以我们可以用STL中的map来存储这一个<指数，系数>键值对。

因此我在此设了三个map数组

map<int,double> a;    //多项式A（最后的余数）
map<int,double> b;    //除数
map<int,double> c;    //商

多项式A的初始化

 cin>>lena;    //A多项式的项数
 for(int i=;i<lena;i++){
     int e;
     double c;
     cin>e;
     cin>>c;
     maxe_a = max(maxe_a,e);//找到A的最高次指数
     a[e] = a[e] + c;    //相同系数即刻合并
 }

多项式B同理，但要注意多求一个最小项次数。

接下来，最重要的来了，那就是除法运算的过程。首先我们先知道要进行几次除法的运算。由上面的示例步骤我们可以知道，运算次数为：（ A的最高次幂 - B的最高次幂 ）+ 1 次，也可理解为（ i = max （e_A）; i >= max（e_B）; i --）这样的过程。

商的其中一项就是（当前A的最高次幂系数 / B的最高次幂系数）这是系数，指数为 （当前A的最高次幂 - B的最高次幂），为什么加一个当前呢？因为A每次最高项都会被（B的最高次项 * 相应商的一项）所消掉，直至A最终变为要求的余数项为止。

余数项，就是A每一项每次被 （B的每项 * 相应项的商）做差后系数没被削成0的项。

 for(int i = maxe_a;i>=maxe_b;i--){
     if(b[maxe_b]!=){
         div = 1.0*a[i]/b[maxe_b];
         //printf("div=%.1lf\n",div);
         sub = i - maxe_b;
         c[sub] = div;
         maxe_c = max(maxe_c,sub);    //求商的最高次幂
                  //每次从剩余项的最高次开始，直到B的最低次，每项做差
         for(int j=i;j>=mine_b;j--){
             if(j-sub >= ){
                 a[j] = a[j] - b[j-sub]*c[sub];
             }
         }
     }
 }

之后c[ ] 就是商，a[ ] 就是余数项。

最后依据题意，为c[ ]数组 a[ ]数组做下四舍五入。接下来讲一下怎么做四舍五入。

因为题目要求保留一位有效数字，所以就先把这个数*10化为（int）+/-0.5，再除以10即可。今后碰见四舍五入问题一次类推！

for(int i=maxe_c;i>=;i--){
    //四舍五入处理
    c[i] = (double)((int)(c[i]* + (c[i]<?-0.5:0.5)))/;
    if(c[i]){
        cnt++;
    }
}   

最后奉上此题解的原码：

 #include<cstdio>
 #include<iostream>
 #include<map>
 #include<algorithm>
 #include<cmath>
 using namespace std;

 map<int,double> a;
 map<int,double> b;
 map<int,double> c;
 int lena,lenb;

 int main(){
     int maxe_a = ,mine_b=,maxe_b=,maxe_c=;
     double div;
     int sub;
     cin>>lena;
     for(int i=;i<lena;i++){
         int e;
         double c;
         cin>>e;
         cin>>c;
         maxe_a = max(maxe_a,e);    //找到A的最高次指数
         a[e] = a[e] + c;    //相同系数即刻合并
     }
     cin>>lenb;
     for(int i=;i<lenb;i++){
         int e;
         double c;
         cin>>e;
         cin>>c;
         mine_b = min(mine_b,e);    //找到B的最低次指数
         maxe_b = max(maxe_b,e);    //找到B的最高次指数
         b[e] = b[e] + c;    //相同系数即刻合并
     }
     for(int i = maxe_a;i>=maxe_b;i--){
         if(b[maxe_b]!=){
             div = 1.0*a[i]/b[maxe_b];
             //printf("div=%.1lf\n",div);
             sub = i - maxe_b;
             c[sub] = div;
             maxe_c = max(maxe_c,sub);    //求商的最高次幂
             for(int j=i;j>=mine_b;j--){        //每次从剩余项的最高次开始，直到B的最低次，每项做差
                 if(j-sub >= ){
                     a[j] = a[j] - b[j-sub]*c[sub];
                 }
             }
         }
     }
     int cnt=;
     for(int i=maxe_c;i>=;i--){
         c[i] = (double)((int)(c[i]* + (c[i]<?-0.5:0.5)))/;//四舍五入处理
         if(c[i]){
             cnt++;
         }
     }
     if(cnt ==){
         printf("0 0 0.0\n");
     }else{
         printf("%d",cnt);
         for(int i=maxe_c;i>=;i--){
             if(c[i]){
                 printf(" %d %.1lf",i,c[i]);
             }
         }
         printf("\n");
     }
     cnt =;
     for(int i = maxe_a;i>=;i--){
         a[i] = (double)((int)(a[i]* + (a[i]<?-0.5:0.5)))/;//四舍五入处理
         if(a[i]){
             cnt++;
         }
     }
     if(cnt ==){
         printf("0 0 0.0");
     }else{
         printf("%d",cnt);
         for(int i=maxe_a;i>=;i--){
             if(a[i]){
                 printf(" %d %.1lf",i,a[i]);
             }
         }
     }
     return ;
 }

---

最后总结一下，像这题可以作为多项式相除的模板题目。以后还可用于多项式的因式分解，求方程根等问题。

参考：cccc L2-018. 多项式A除以B