Java实现 LeetCode 51 N皇后

51. N皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

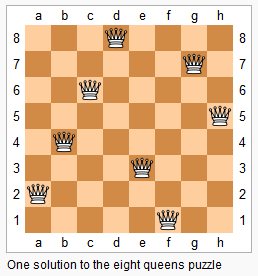
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例:

输入: 4

输出: [

[".Q…", // 解法 1

“…Q”,

“Q…”,

“…Q.”],

["…Q.", // 解法 2

“Q…”,

“…Q”,

“.Q…”]

]

解释: 4 皇后问题存在两个不同的解法。

class Solution {
     public static List<List<String>> output;
    public List<List<String>> solveNQueens(int n) {
        output = new ArrayList<>();
        // 声明一个长度为n的数组用来代表 第n行棋子是在第result[n]列
        int[] result = new int [n];
        calnQueens(0, n, result);
        return output;
    }

    // n 皇后问题 row代表计算到了到第row行
    private static void calnQueens(int row, int n, int[] result){
        if (row == n){
            // 到达第n行代表已经得到一个将解决方案 直接返回即可
            // 根据result数组将结果加入到output列表中
            getPrint(result);
            return;
        }
        // 若不是第n行 则说明需要继续判断该行棋子应该在那一列
        for (int column = 0; column < n; column++){
            // 判断第row行 放置在column列的棋子是否满足要求
            if (isOK(row, column, result)){
                result[row] = column;
                // 递归判断下一行的情况
                calnQueens(row + 1, n, result);
            }
            // 不满足要求 回溯下一列 对应操作column++
        }
    }

    // row代表行数 column代表列数 result代表满足规则的棋子在第n行中的位置
    private static boolean isOK(int row, int column, int[] result){
        // 判断棋子的位置是否正确 不正确返回false
        for (int i = 0; i < row; i++){
            // 第一个条件排除的是相同列的问题
            // 第二个条件排除的是对角线列的左下角
            // 第三个条件排除的是对角线列的右下角
            if (column == result[i] || column == result[i] - row + i || column == result[i] + row - i){
                return false;
            }
        }
        return true;
    }

    private static void getPrint(int[] result){
        List<String> one = new ArrayList<>();
        for (int row = 0; row < result.length; row++){
            // 一行一个StringBuilder
            StringBuilder str = new StringBuilder();
            for (int column = 0; column < result.length; column++){
                if (column == result[row]){
                    str.append("Q");
                }else{
                    str.append(".");
                }
            }
            one.add(str.toString());
        }
        output.add(one);
    }
}