数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法

算法复杂度主方法

有时候，我们要评估一个算法的复杂度，但是算法被分散为几个递归的子问题，这样评估起来很难，有一个数学公式可以很快地评估出来。

一、复杂度主方法

主方法，也可以叫主定理。对于那些用分治法，有递推关系式的算法，可以很快求出其复杂度。

定义如下：

如果对证明感兴趣的可以翻阅书籍：《算法导论》。如果觉得太难思考，可以跳过该节。

由于主定理的公式十分复杂，所以这里有一种比较简化的版本来计算：

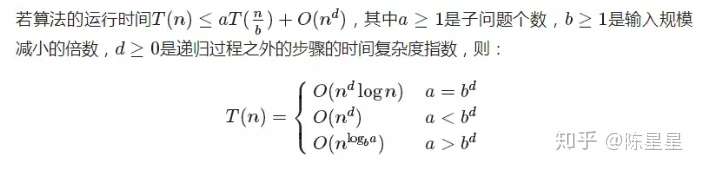
二、举例

1. 二分搜索，每次问题规模减半，只查一个数，递推过程之外的查找复杂度为O(1)，递推运算时间公式为：T(n) = T(n/2) + O(1)。
2. 快速排序，每次随机选一个数字作为划分进行排序，每次问题规模减半，递推过程之外的排序复杂度为O(n)，递推运算时间递推公式为：T(n) = 2T(n/2) + O(n)。

按照简化版的主定理，可以知道：

二分查找：a = 1，b = 2，d = 0，可以知道a = b^d，所以二分查找的时间复杂度为：O(logn)。

快速排序：a = 2，b = 2，d = 1，可以知道a = b^d，所以快速排序的时间复杂度为：O(nlogn)。

强调：并非所有递推关系式都可应用主定理，但是大部分情况下都可以。

因为需要较多的数学知识，所以我们只简单介绍到这里。

延伸-计算理论：P和NP问题

在计算机科学中，有一个专门的分支研究问题的可计算性，叫做计算理论。

我们用计算机算法来解决一个问题，如果一个问题被证明很难计算，或者只能暴力枚举来解决，那么我们就不必花大力气去质疑使用的算法是不是错了，为什么这么慢，计算怎么久都没出结果，到底有没有更好的算法。

计算机科学把一个待解决的问题分类为：P问题，NP问题，NPC问题，NP-hard问题。

一、P 和 NP 问题

类似于O(1)，O(logn)，O(n)等复杂度，规模n出现在底数的位置，计算机能在多项式时间解决，我们称为多项式级的复杂。

类似于O(n!)，O(2^n)等复杂度，规模n出现在顶部的位置，计算机能在非多项式时间解决，我们称为非多项式级的复杂度。

如果一个问题，可以用一个算法在多项式时间内解决，它称为P问题(P为Polynominal的缩写，多项式)。

比如求1加到100的总和，它的时间复杂度是O(n)，是多项式时间。

然而有些问题，只能用枚举的方式求解，时间复杂度是指数级别，非多项式时间，但是只要有一个解，我们能在多项式时间验证这个解是对的，这类问题称为NP问题。

也就是说，如果我们只能靠猜出问题的一个解，然后可以用多项式时间来验证这个解，这些问题都是NP问题。

所以，按照定义，所有的P问题都是NP问题。

计算理论延伸出了图灵机理论，自动机=算法。

有两种自动机，一种是确定性自动机，机器从一个状态到另外一个状态的变化，只有一个分支可以走，而非确定性自动机，从一个状态到另外一个状态，有多个分支可以走。P问题都可以用两种机器来解决，当非确定性自动机退化就变成了确定性自动机，而NP问题只能用非确定性自动机来解决。

自动机对N和NP问题的定义：

可以在确定性自动机以多项式时间解决的问题，称为P问题，可以在多项式时间验证答案的问题称为NP问题。而NP问题是可以在非确定型自动机以多项式时间解决的问题（NP两字为Non-deterministicPolynomial的缩写，非确定多项式）。

数学，计算机科学，哲学，三个学科其实交融在一起，自动机是一台假想的机器，世界其实也可以认为是一个假想的机器，所以世界可以等于一台自动机吗，大家可以发挥想象力，在以后的日子里慢慢体会，建议购买书籍《计算理论》补习相关知识。

二、NPC 和 NP-hard 问题

存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件：

1. 它得是一个NP问题。
2. 所有的NP问题都可以约化到它。

这种问题称为NP完全问题（NPC）。按照这种定义，NP问题要比NPC问题的范围广。

那什么是NP-hard问题，其定义要满足2个条件：

1. 所有的NP问题都可以约化到它。
2. 它不是一个NP问题。

也就是说，NP-hard问题更难，你只要解决了NP-hard问题，那么所有的NP问题都可以解决。但是，这个问题本身不是一个NP问题，也就是解不能在多项式时间内被验证。

比如你有一个交际网，每个人是一个节点，认识的人之间相连。你要通过一个最快、最省钱、最能提升你个人形象、最没有威胁、最不影响你日常生活的方式认识一个萌妹，你怎么证明你认识这个萌妹是最省钱的呢？-来自知乎回答。

我们一旦发现一个问题是NPC问题，那么我们很难去准确求出其解，只能暴力枚举，靠猜。

三、总结

各类问题可以用这个图来表示：

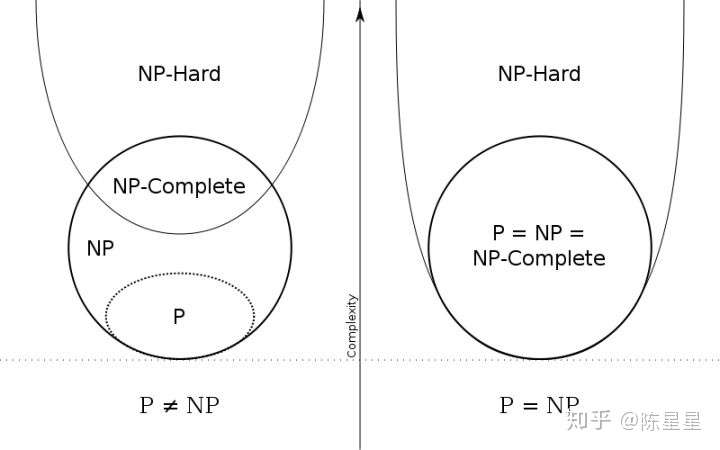
"P=NP" 问题的目标，就是想要知道P和NP这两个集合是否相等。为了证明两个集合（A和B）相等，一般都要证明两个方向：

1. A包含B。
2. B包含A。

我们已经说过NP包含了P。因为任何一个非确定性机器，都能被当成一个确定性的机器来用。你只要不使用它的“超能力”，在每个分支点只探索一条路径就行。

所以 "P=NP" 就在于P是否也包含了NP。也就是说，如果只使用确定性计算机，能否在多项式时间之内，解决所有非确定性计算机能在多项式时间内解决的问题。

系列文章入口

我是陈星星，欢迎阅读我亲自写的 数据结构和算法(Golang实现)，文章首发于 阅读更友好的GitBook。

• 数据结构和算法(Golang实现)(1)简单入门Golang-前言
• 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
• 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
• 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
• 数据结构和算法(Golang实现)(5)简单入门Golang-接口
• 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
• 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
• 数据结构和算法(Golang实现)(8.1)基础知识-前言
• 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
• 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
• 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
• 数据结构和算法(Golang实现)(11)常见数据结构-前言
• 数据结构和算法(Golang实现)(12)常见数据结构-链表
• 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
• 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
• 数据结构和算法(Golang实现)(15)常见数据结构-列表
• 数据结构和算法(Golang实现)(16)常见数据结构-字典
• 数据结构和算法(Golang实现)(17)常见数据结构-树
• 数据结构和算法(Golang实现)(18)排序算法-前言
• 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
• 数据结构和算法(Golang实现)(20)排序算法-选择排序
• 数据结构和算法(Golang实现)(21)排序算法-插入排序
• 数据结构和算法(Golang实现)(22)排序算法-希尔排序
• 数据结构和算法(Golang实现)(23)排序算法-归并排序
• 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
• 数据结构和算法(Golang实现)(25)排序算法-快速排序
• 数据结构和算法(Golang实现)(26)查找算法-哈希表
• 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
• 数据结构和算法(Golang实现)(28)查找算法-AVL树
• 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
• 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树