「USACO5.4」奶牛的电信Telecowmunication

传送门

Luogu

解题思路

题目要求的是最小割点集，考虑用最小割来做。

所有边容量为1，直接求最小割？

这样肯定会出错，比如这种情况：



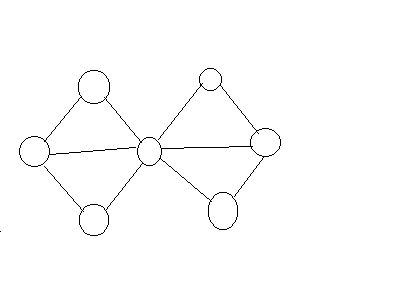
从最左边的点到最右边的点的最小割为2，但是答案是1，只要破坏中间那个点就好了。

所以我们把删点转化为割边。

考虑拆点：方便起见，我们把拆出来的点称作“次点”。

那么对于每个点都向它的次点连一条容量为1的边。

然后对于原图中的边 \(u \to v\)，连边 \(u^\prime \to v,v^\prime \to u\)，容量都为inf。

也就是我们保证到达一个点的流量只能从原点入，次点出，那么我们割掉他们之间的边，就相当于删掉了这个点。

细节注意事项

• 源点是输入的源点的次点

参考代码

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <cmath>
#include <ctime>
#include <queue>
#define rg register
using namespace std;
template < class T > inline void read(T& s) {
	s = 0; int f = 0; char c = getchar();
	while (!isdigit(c)) f |= c == '-', c = getchar();
	while (isdigit(c)) s = s * 10 + c - 48, c = getchar();
	s = f ? -s : s;
}

const int _ = 10002;
const int __ = 100002;
const int INF = 2147483647;

int tot = 1, head[_], nxt[__ << 1], ver[__ << 1], cap[__ << 1];
inline void Add_edge(int u, int v, int d)
{ nxt[++tot] = head[u], head[u] = tot, ver[tot] = v, cap[tot] = d; }
inline void link(int u, int v, int d) { Add_edge(u, v, d), Add_edge(v, u, 0); }

int n, m, s, t, dep[_];

inline int bfs() {
	static queue < int > Q;
	memset(dep + 1, 0, sizeof (int) * 2 * n);
	dep[s] = 1, Q.push(s);
	while (!Q.empty()) {
		int u = Q.front(); Q.pop();
		for (rg int i = head[u]; i; i = nxt[i]) {
			int v = ver[i];
			if (dep[v] == 0 && cap[i] > 0)
				dep[v] = dep[u] + 1, Q.push(v);
		}
	}
	return dep[t] > 0;
}

inline int dfs(int u, int flow) {
	if (u == t) return flow;
	for (rg int i = head[u]; i; i = nxt[i]) {
		int v = ver[i];
		if (dep[v] == dep[u] + 1 && cap[i] > 0) {
			int res = dfs(v, min(flow, cap[i]));
			if (res) { cap[i] -= res, cap[i ^ 1] += res; return res; }
		}
	}
	return 0;
}

inline int Dinic() {
	int res = 0;
	while (bfs()) while (int d = dfs(s, INF)) res += d;
	return res;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif
	read(n), read(m), read(s), read(t), s += n;
	for (rg int i = 1; i <= n; ++i) link(i, i + n, 1);
	for (rg int u, v, i = 1; i <= m; ++i)
		read(u), read(v), link(u + n, v, INF), link(v + n, u, INF);
	printf("%d\n", Dinic());
	return 0;
}

完结撒花 \(qwq\)