Fibonacci 数列算法分析

 /*************************************************
 *  Fibonacci 数列算法分析
 *************************************************/
 #include<iostream>
 #include<stdio.h>
 #include<vector>
 #include<cmath>
 #include<time.h>
 using namespace std;
 #define Time 1000000
 #define N 15
 #define Echo printf("result：%d | spend：%.3f\n",a,(((double)(clock()-start))/1000))
 #define For for(int i=1; i<Time; ++i)
 /*************************************************
 Function:       fibo1 fibo2 fibo3  fibo4
 defferent:      1递归 2迭代 3向量 4公式
 Description:    斐波那契数列求值
 Return:         返回第N项的值
 *************************************************/
 int fibo1(int n) {
     if(n==)return ;
     if(n==)return ;
     return fibo1(n-)+fibo1(n-);
 }
 int fibo2(int n) {
     int a=,c;
     for(int b=,i=; i<=n; ++i)
         c=a+b,a=b,b=c;
     return c;
 }
 int fibo3(int n) {
     vector<int> v(n+,);
     v[]=;
     for(int i=; i<=n; ++i)
         v[i]=v[i-]+v[i-];
     return v[n];
 }
 int fibo4(int n) {
     return (pow((+sqrt(5.0))/,n)-pow((-sqrt(5.0))/,n))/sqrt(5.0);
 }

 int main() {
     int a;

     clock_t start=clock();
     For a=fibo1(N);
     Echo;

     start=clock();
     For a=fibo2(N);
     Echo;

     start=clock();
     For a=fibo3(N);
     Echo;

     start=clock();
     For a=fibo4(N);
     Echo;

     return ;
 }

循环次数 100000 ，N 为 10 结果如下

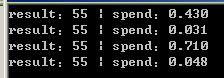
循环次数 100000 ，N 为 15 结果如下

-循环次数 100000 ，N 为 20 结果如下

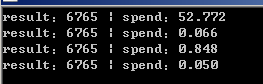
可以看出递归最为耗时：代码简单易懂

向量由于做了大量的下标工作，相对来说次之

公式法再次之（在N=15时，公式法与迭代法性能不确定）：公式推导，性能具有良好的稳定性

迭代最优：编程复杂，效率较高

以上只是针对本次测试