PCA主成分分析的矩阵原理

【前言】主成分分析（PCA）实现一般有两种，一种是对于方阵用特征值分解去实现的，一种是对于不是方阵的用奇异值（SVD）分解去实现的。

一、特征值

　　特征值很好理解，特征值和特征向量代表了一个矩阵最鲜明的特征方向。多个特征值和特征向量的线性组合可以表示此矩阵。选取特征值最大的特征值对应的特征向量，此特征向量在组成矩阵的线性组合中所占的比重是最大的。一般选取前一半就可，实现降维。

二、奇异值

　　这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量。我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：

 

 

    这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。
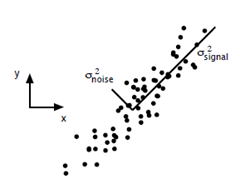
    一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。
　　PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
 　 1、还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

　　2、而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：

　　3、但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

　　4、在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子：

　　5、将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

　　

　　6、这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U'：

    7、这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了。

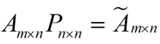
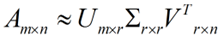
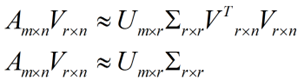
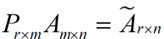
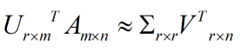
三、总结

　　而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。