Codeforces Round #665 (Div. 2) D - Maximum Distributed Tree dfs贡献记录

题意：

t组输入，每组数据中n个节点构成一棵树，然后给你n-1条边。给你一个m，然后给你m个k的素数因子，你需要给这n-1条边都赋一个权值，这n-1条边的权值之积应该等于k。如果k的素数因子数量小于n-1，那可以使用1来填充

然后我们定义F(x,y)为节点x到节点y的路径上所有边的和

我们要求出来所有任意两点之间的F(x,y)，然后把所有F(x,y)加起来输出，求最大结果是多少，结果取余1e9+7

题解：

因为我们要使

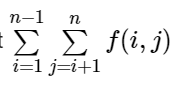
这个尽可能大，所以肯定要按那一条边使用次数最多，我们就把最大那个素数因子给这一条边，这样得到的结果肯定最大

怎么处理每一条边的使用次数，可以使用dfs遍历一遍就可以了

dfs过程中如果遇到叶节点，那么与叶节点相连这条边的使用次数也就是n-1，例如叶节点是1，那么节点1与2，3，4...n这些点构成的路径会经过这条边n-1次

如果不是叶节点，我们首先要在dfs过程中记录一下，这个节点有多少子节点，设为ans，然后ans*(n-ans)就是对与这个节点相连那条边的使用次数

之后再处理一下素数因子，如果素数因子小于n-1，那么就需要补加上n-m+1个1

如果素数因子大于n-1，那么就让多的素数因子乘起来变成一个

dfs的根节点，就随便找一个叶节点就行

代码：

#include<stack>
#include<queue>
#include<map>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#define fi first
#define se second
#define pb push_back
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
const int mod=1e9+7;
const double eps=1e-8;
const int INF = 0x3f3f3f3f;
vector<ll>w[maxn],L;
ll p[maxn],n,root,m;
void add_edge(ll x,ll y)
{
    w[x].push_back(y);
    w[y].push_back(x);
}
ll dfs(ll x,ll fa)
{
    ll len=w[x].size(),ans=0;
    if(len==1 && x!=root)
    {
        L.push_back(n-1);
        return 1;
    }
    for(ll i=0; i<len; ++i)
    {
        ll y=w[x][i];
        if(y==fa) continue;
        ll temp=dfs(y,x);
        ans+=temp;
    }
    ans++;
    //printf("%lld %lld*****\n",x,1);
    //printf("%lld***%lld\n",ans,ans*(n-ans));
    if(x!=root)
    {

        L.push_back(ans*(n-ans));
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    ll t;
    cin>>t;
    while(t--)
    {
        ll m,sum=0;
        //num=1;
        root=1;
        L.clear();
        //scanf("%lld",&n);
        cin>>n;
        for(ll i=1; i<=n; ++i)
            w[i].clear();
        for(ll i=1; i<n; ++i)
        {

            ll x,y;
            //scanf("%lld%lld",&x,&y);
            cin>>x>>y;
            add_edge(x,y);
        }
        //scanf("%lld",&m);
        cin>>m;
        for(ll i=1; i<=m; ++i)
        {
            //scanf("%lld",&p[i]);
            cin>>p[i];
        }
        for(ll i=1; i<=n; ++i)
        {
            if(w[i].size()==1)
            {
                root=i;
                break;
            }
        }
        dfs(root,-1);
        sort(p+1,p+1+m,greater<ll>());
        sort(L.begin(),L.end(),greater<ll>());
        ll d=0;
        if (m > n - 1)
        {
            d = m - n + 1;
            for (ll i = 1; i <= d; i++)
            {
                p[i + 1] = p[i + 1] * p[i] % mod;
            }
        }
        if (m < n - 1)
        {
            for (ll i = m + 1; i <= n - 1; i++)
            {
                p[i] = 1;
            }
        }//printf("*********\n");
        sum=0;
        for(ll i=1;i<n;++i)
        {
            //printf("%lld %lld\n",que[i],p[i]);
            sum=sum+L[i-1]*p[i+d];
            sum = (sum + mod) % mod;
        }
        cout<<sum<<endl;
    }
    return 0;
}