Codeforces ECR86 C. Yet Another Counting Problem(规律,区间)

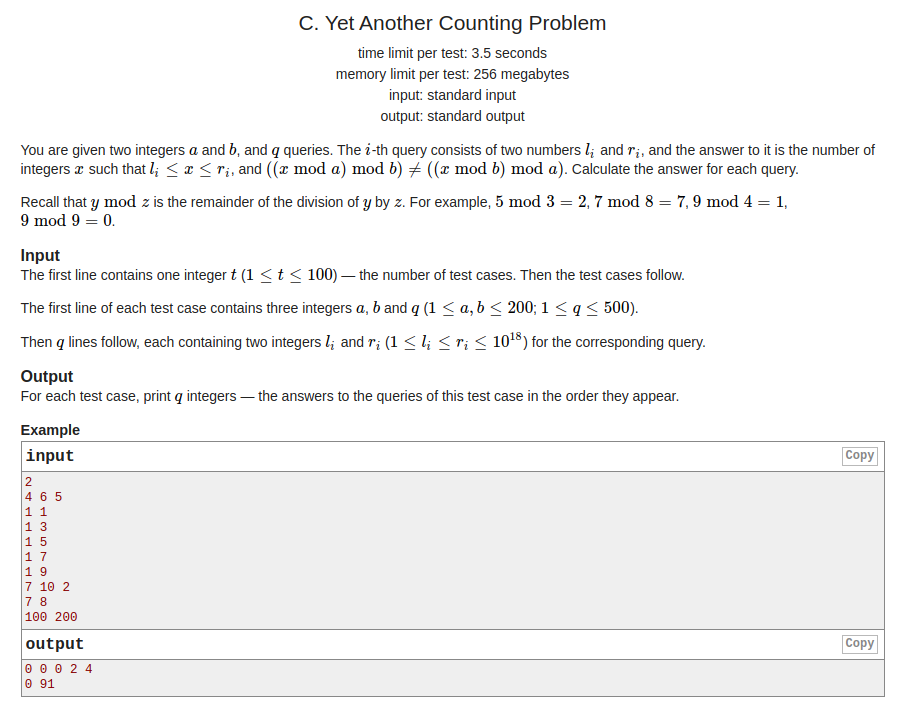
题意:给你两个正整数a和b,询问q次,每次给你一个区间[l,r],问[l,r]中有多少数字满足:x%a%b!=a%b%a.

题解:看公式无从下手的题,一般都是要找规律的.首先,我们知道,假如x%a%b!=x%b%a,那么:(x+lcm(a,b))%a%b!=(x+lcm(a,b))%b%a,(这个知识在exgcd中很常用).所以,我们打表发现,这其实是一个循环节的问题.

　　　首先枚举[1,lcm]中有多少不相同的,然后每次询问,我们处理一下区间就好了,公式:(r/lcm-(l-1)/lcm)*num[lcm]+num[r%lcm]-num[(l-1)%lcm]

　代码:

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #include <algorithm>
 6 #include <stack>
 7 #include <queue>
 8 #include <vector>
 9 #include <map>
10 #include <set>
11 #include <unordered_set>
12 #include <unordered_map>
13 #define ll long long
14 #define fi first
15 #define se second
16 #define pb push_back
17 #define me memset
18 const int N = 1e6 + 10;
19 const int mod = 1e9 + 7;
20 using namespace std;
21 typedef pair<int,int> PII;
22 typedef pair<long,long> PLL;
23
24 int t;
25 ll a,b,q;
26 ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
27 ll l,r;
28 ll num[N];
29 ll lcm;
30
31 int main() {
32     ios::sync_with_stdio(false);
33     cin>>t;
34      while(t--){
35          cin>>a>>b>>q;
36          lcm=a*b/gcd(a,b);
37          for(int i=1;i<=lcm;++i){
38              num[i]=num[i-1];
39               if(i%a%b!=i%b%a) num[i]++;
40          }
41          while(q--){
42              cin>>l>>r;
43               printf("%lld ",(r/lcm-(l-1)/lcm)*num[lcm]+num[r%lcm]-num[(l-1)%lcm]);
44          }
45          puts("");
46      }
47     return 0;
48 }