[BFS]骑士旅行

骑士旅行

Description

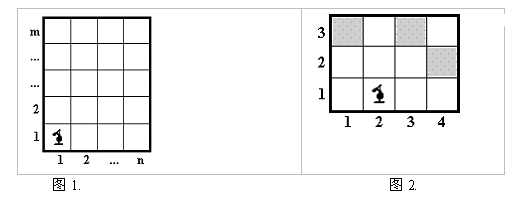
在一个n m 格子的棋盘上，有一只国际象棋的骑士在棋盘的左下角 (1;1)(如图1)，骑士只能根据象棋的规则进行移动，要么横向跳动一格纵向跳动两格，要么纵向跳动一格横向跳动两格。 例如， n=4，m=3 时，若骑士在格子(2;1) (如图2), 则骑士只能移入下面格子：(1;3),(3;3) 或 (4;2)；对于给定正整数n，m，I，j值 (m,n<=50,I<=n,j<=m) ，你要测算出从初始位置(1;1) 到格子(i;j)最少需要多少次移动。如果不可能到达目标位置，则输出"NEVER"。

---

Input

输入文件的第一行为两个整数n与m，第二行为两个整数i与j。

---

Output

输出文件仅包含一个整数为初始位置(1;1) 到格子(i;j)最少移动次数。

---

Sample Input

5 3
1 2

---

Sample Output

3

---

代码

#include<stdio.h>
#include<iostream>
using namespace std;
const int dx[9]={0,2,2,1,1,-1,-1,-2,-2};
const int dy[9]={0,-1,1,-2,2,-2,2,-1,1}; //可以延伸的八个方向
bool f=false;
int n,m,ii,jj,st[1005][4],fa[1005],a[1005][1005];
void bfs(){
    int head=0,tail=1;
    st[1][1]=1;st[1][2]=1;st[1][3]=0;a[1][1]=1; //st[][1]和st[][2]是记录位置，st[][3]是记录走了多少步
    do{
    	head++;
        for(int i=1;i<=8;i++){
            int x=st[head][1]+dx[i];
            int y=st[head][2]+dy[i];
            if(a[x][y]==0) //判断有没有走过
             if(x>0 and y>0 and x<=n and y<=m){ //判断这个点能不能走
                 tail++;
                 a[x][y]=1; //标记走过了
                 st[tail][1]=x;
                 st[tail][2]=y;
                 st[tail][3]=st[head][3]+1;  //记录
             }
             if(x==ii and y==jj){ //判断有没有到达终点
             	f=true;
                printf("%d\n",st[tail][3]);
                return ;
             }
        }
    }while(head<=tail);
}
int main(){
    scanf("%d%d",&n,&m);
    scanf("%d%d",&ii,&jj);
    bfs();
    if(!f)printf("NEVER"); //如果不能达到就输出"NEVER"
    return 0;
}