洛谷P2602 [ZJOI2010]数字计数 题解

题目描述

输入格式

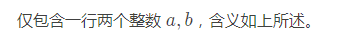
输出格式

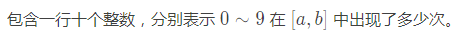
输入输出样例

输入样例

1 99

输出样例

9 20 20 20 20 20 20 20 20 20

说明/提示

数据规模与约定

分析

很裸的一道数位DP的板子

定义f[当前枚举到的数位][当前数位之前的答案][枚举的数字]

其它的套板子就可以了，要注意一下前缀0的判断

代码

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 #include<queue>
 #include<cmath>
 using namespace std;
 typedef long long ll;
 ll f[][][],num[];
 ll a,b;
 ll asd(ll now,ll tot,ll ask,ll jud,ll zer){
     if(now<){
         return tot;
     }
     if(f[now][tot][ask]!=- && jud== &&(ask || !zer)){
         return f[now][tot][ask];
     }
     ll mmax=;
     if(jud==) mmax=num[now];
     ll anss=;
     for(ll i=;i<=mmax;i++){
         anss+=asd(now-,tot+( (i==ask) & (!zer || i)),ask,jud&(i==mmax),zer&(i==));
     }
     if(!jud && (ask || !zer)) f[now][tot][ask]=anss;
     return anss;
 }
 ll solve(ll xx,ll ask){
     ll cnt=;
     memset(num,,sizeof(num));
     while(xx){
         ll aa=xx%;
         num[cnt++]=aa;
         xx/=;
     }
     return asd(cnt-,,ask,,);
 }
 int main(){
     memset(f,-,sizeof(f));
     scanf("%lld%lld",&a,&b);
     for(ll i=;i<=;i++){
         ll ans=solve(b,i)-solve(a-,i);
         printf("%lld ",ans);
     }
     printf("\n");
     return ;
 }