[luogu4478 BJWC2018] 上学路线 (容斥原理+拓展lucas)

传送门

Description

小B 所在的城市的道路构成了一个方形网格，它的西南角为(0,0)，东北角为(N,M)。

小B 家住在西南角，学校在东北角。现在有T 个路口进行施工，小B 不能通过这些路口。小B 喜欢走最短的路径到达目的地，因此他每天上学时都只会向东或北行走；而小B又喜欢走不同的路径，因此他问你按照他走最短路径的规则，他可以选择的不同的上学路线有多少条。由于答案可能很大，所以小B 只需要让你求出路径数mod P 的值。

Input

第一行为四个整数N、M、T、P。

接下来的T 行，每行两个整数，表示施工的路口的坐标。

Output

一行一个整数，表示路径数mod P 的值。

Sample Input

3 4 3 1019663265

3 0

1 1

2 2

Sample Output

8

HINT

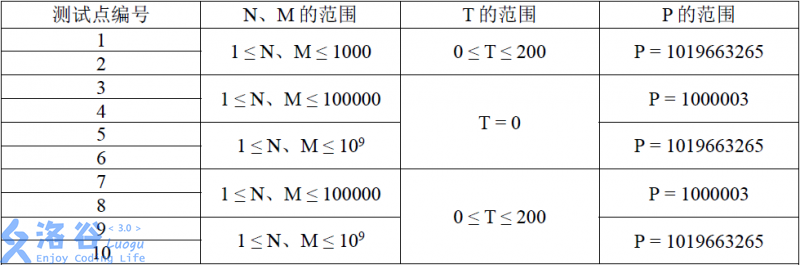
Solution

f[i]表示从（0,0）到第i个施工点的可行路径数最终答案为\(f[T+1]\) （设第T+1个为（n,m））

排序后每次用全部路径数-到中间某一个施工点（j）的路径数*j到i的路径数

Code

//By Menteur_Hxy
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define x first
#define y second
#define int long long
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
#define R(i,a,b) for(register int i=(b);i>=(a);i--)
using namespace std;
typedef pair<int,int> PII;

int read() {
	int x=0,f=1; char c=getchar();
	while(!isdigit(c)) {if(c=='-')f=-f;c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
	return x*f;
}

const int T=210,mod[5]={1000003,3,5,6793,10007},MOD=1019663265;
bool flag;
int f[T],fac[5][1000010],inv[5][1000010],d[5];
PII da[T];

int qpow(int a,int b,int p) {
	int t=1;
	while(b) {
		if(b&1) t=t*a%p;
		a=a*a%p; b>>=1;
	}
	return t;
}

int lucas(int n,int m,int p) {
	if(n<m) return 0;
	if(n<mod[p]&&m<mod[p]) return fac[p][n]*inv[p][m]%mod[p]*inv[p][n-m]%mod[p];
	return lucas(n/mod[p],m/mod[p],p)*lucas(n%mod[p],m%mod[p],p)%mod[p];
}

int C(int n,int m) {
	if(!flag) return lucas(n,m,0);
	int ans=0;
	F(i,1,4) ans=(ans+MOD/mod[i]*qpow(MOD/mod[i],mod[i]-2,mod[i])%MOD*lucas(n,m,i)%MOD)%MOD;
	return ans;
}

signed main() {
	int n=read(),m=read(),t=read(),p=read(); flag=(p==MOD);
	F(i,0,4) {
		fac[i][0]=1;
		F(j,1,mod[i]-1) fac[i][j]=fac[i][j-1]*j%mod[i];
		inv[i][mod[i]-1]=qpow(fac[i][mod[i]-1],mod[i]-2,mod[i]);
		R(j,-1,mod[i]-2) inv[i][j]=inv[i][j+1]*(j+1)%mod[i];
	}
	F(i,1,t) {int a=read(),b=read();da[i]=PII(a,b);} da[++t].x=n,da[t].y=m;
	sort(da+1,da+1+t);
	F(i,1,t) {
		f[i]=C(da[i].x+da[i].y,da[i].x);
		F(j,1,i-1) if(da[j].y<=da[i].y)
			f[i]=(f[i]-f[j]*C(da[i].x+da[i].y-da[j].x-da[j].y,da[i].x-da[j].x)%p+p)%p;
	}
	printf("%lld",f[t]);
	return 0;
}