来去学习之---KMP算法--next计算过程

一、概述

KMP算法是一种字符串匹配算法，比如现有字符串

T：ABCDABCDABCDCABCDABCDE，

P：ABCDABCDE

P字符串对应的next值：[0,0,0,0,1,2,3,4,0]

二、匹配过程

判断T字符串是否包含P字符串？下面看一下KMP的比较过程：

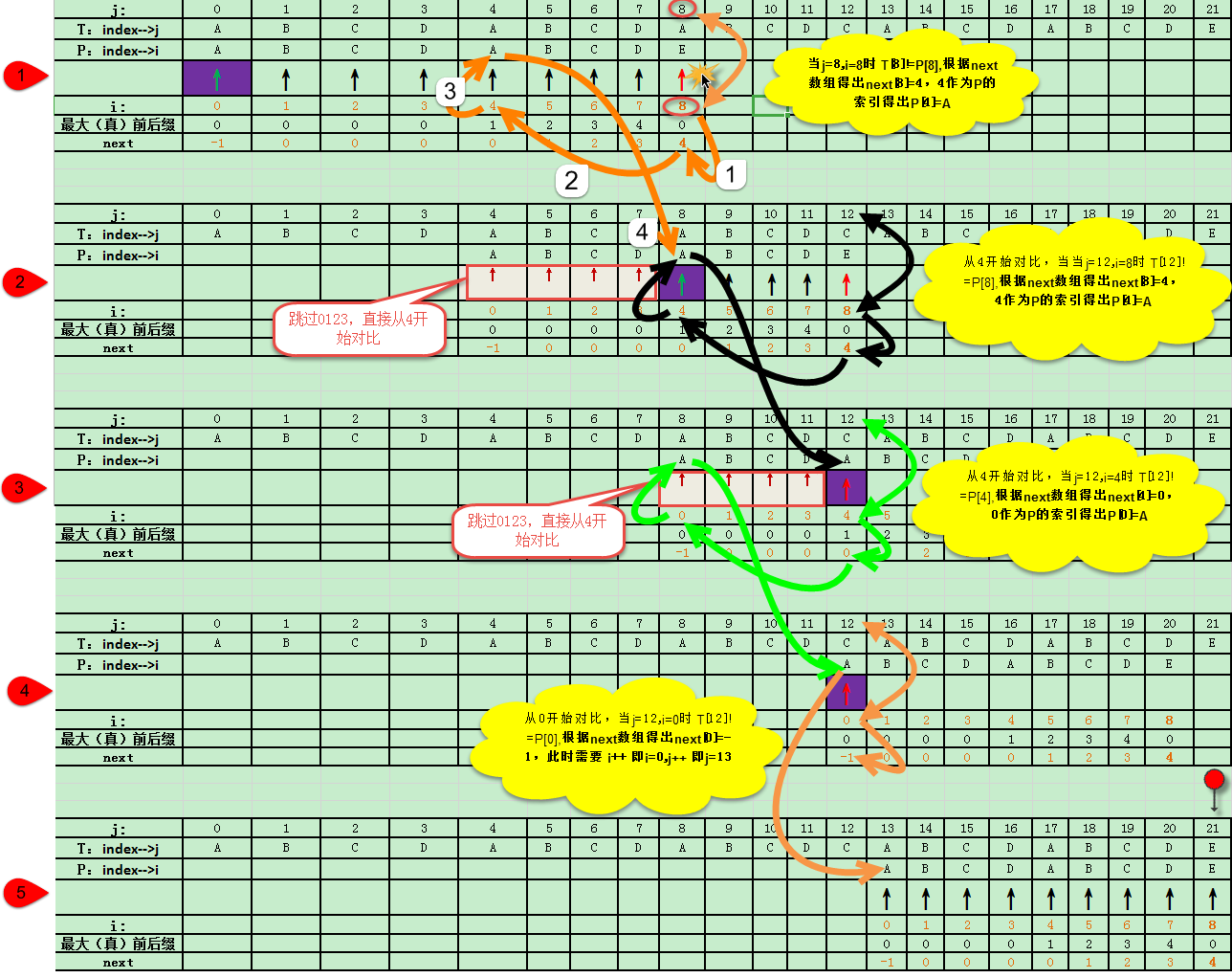
三、next数组计算过程

先了解一下字符串的前后缀（具体来说是真前后缀即 前缀不包含最后一个字符；后缀不包含第一个字符）

字符串	真前缀	真后缀	真前、后缀中相 同的字符串	真前、后缀中 最大相同串	真前、后缀中最 大相同串字符数
abc	a,ab	bc,c	无	无	0
aaa	a,aa	aa,a	a,aa	aa	2
aba	a,ab	ba,a	a	a	1
abab	a,ab,aba	bab,ab,b	ab	ab	2
ababab	a,ab,aba,abab,ababa	babab,abab,bab,ab,b	ab,abab	abab	4

那“ABCDABCDE”字符串的最大真前后缀的计算过程如下：

子串	真前缀字符串	真后缀字符串	真前、后缀中最 大相同串字符	真前、后缀中最 大相同串字符数
A	无	无	无	0
AB	A	B	无	0
ABC	AB、A	BC、C	无	0
ABCD	ABC、AB、A	BCD、CD、D	无	0
ABCDA	ABCD、ABC、AB、A	BCDA、CDA、DA、A	A=A	1
ABCDAB	ABCDA、ABCD、ABC、AB、A	BCDAB、CDAB、DAB、AB、B	AB=AB	2
ABCDABC	ABCDAB、ABCDA、ABCD、 ABC、AB、A	BCDABC、CDABC、DABC、 ABC、BC、C	ABC=ABC	3
ABCDABCD	ABCDABC、ABCDAB、ABCDA、 ABCD、ABC、AB、A	BCDABCD、CDABCD、DABCD、 ABCD、BCD、CD、D	ABCD=ABCD	4
ABCDABCDE	ABCDABCD、ABCDABC、ABCDAB、 ABCDA、ABCD、ABC、AB、A	BCDABCDE、CDABCDE、DABCDE、 ABCDE、BCDE、CDE、DE、E	无	0

 

由上表得出最大真前后缀的结果为：{0,0,0,0,1,2,3,4,0}

接下来需要把这最大真前后缀值转换为next值

索引	0	1	2	3	4	5	6	7	8
字符串	A	B	C	D	A	B	C	D	E
最大真前后缀数	0	0	0	0	1	2	3	4	0
Next	-1	0	0	0	0	1	2	3	4

通过上面的表格可以发现就是把最大真前后缀的值整体向后以后一位，所以next值为：{-1,0,0,0,0,1,2,3,4},计算出这个next数组之后，接下来在匹配的过程中就可以使用了。

注意：有的人感觉使用最大真前后缀也可以作为next值，这是可以作为的，只是在计算最大真前后缀的逻辑代码相对复杂一点点，并且在匹配使用的时候也会复杂一点点

四、实现代码

计算next值的代码

 1 public static int[] computeNext(char[] chs) {
 2         int i = 0;
 3         int j = -1;
 4         int[] next = new int[chs.length];
 5         next[i] = j;
 6         while (i < chs.length - 1) {
 7             if (j == -1 || chs[i] == chs[j]) {
 8                 i++;
 9                 j++;
10                 next[i] = j;
11             } else {
12                 j = next[j];
13             }
14         }
15         return next;
16     }

计算最大真前后缀的代码：

1 public static int[] getPreSuffix(char[] cs) {
 2         int j = 0;
 3         int i = 1;
 4         int len = cs.length;
 5         int[] preSuffix = new int[len];
 6         preSuffix[1] = 0;
 7         while (i < len) {
 8             if (j == 0) {
 9                 if (cs[j] == cs[i]) {
10                     preSuffix[i] = j + 1;
11                     j++;
12                     i++;
13                 } else {
14                     i++;
15                 }
16             } else {
17                 if (cs[j] == cs[i]) {
18                     preSuffix[i] = j + 1;
19                     j++;
20                     i++;
21                 } else {
22                     j = preSuffix[j - 1];
23                 }
24             }
25         }
26         return preSuffix;
27     }

大家有什么疑问、建议欢迎留言、讨论！