DFA与NFA的等价性，DFA化简

等价性

对于每个NFA M存在一个DFA M’，使得L(M)=L(M’)--------等价性证明，NFA的确定化

假定NFA M=<S, Σ, δ, S 0 , F>，我们对M的状态转换图进行以下改造：

解决初始状态唯一性：引进新的初态结点X和终态结点Y，X,Y∉S，从X到S 0中任意状态结点连一条ε箭弧， 从F中任意状态结点连一条ε箭弧到Y

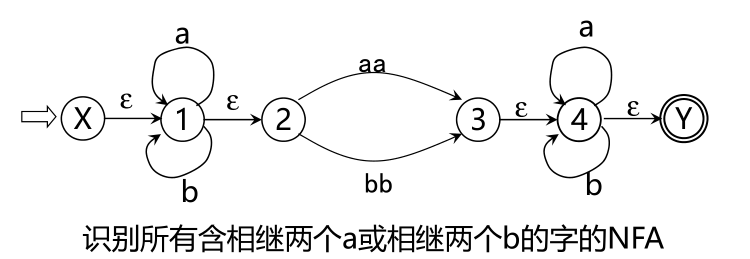
简化弧上的标记：对M的状态转换图进一步施行替换，其中k是新引入的状态

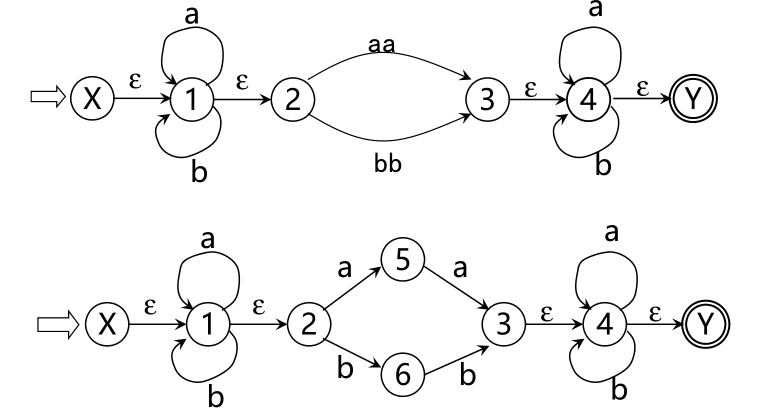
逐步把这个图转变为每条弧只标记为Σ上的一个字符或ε，最后得到一个NFA M’，显然L(M’)=L(M)

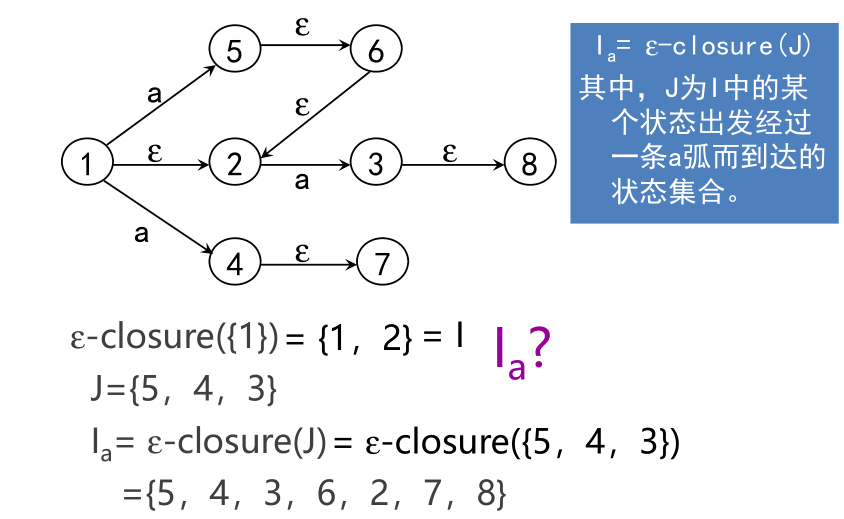
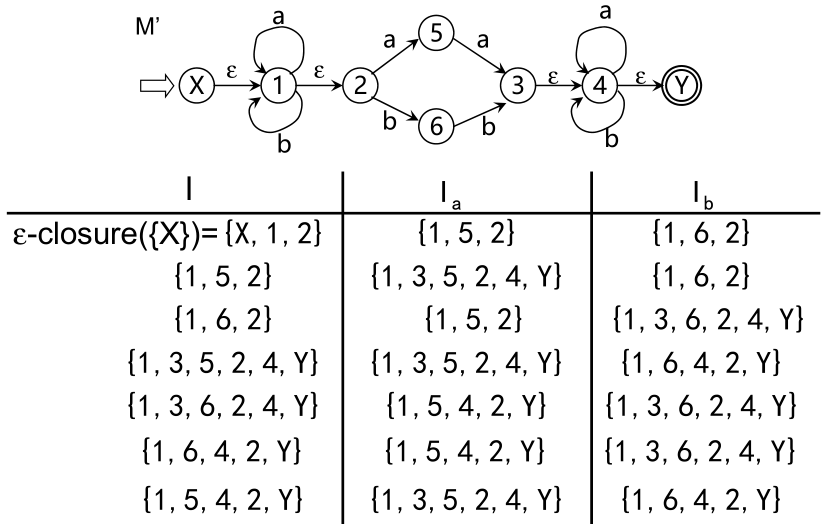
把表看成状态转换矩阵，子集视为状态，转换表唯一刻划了一个确定的有限自动机M，初态是ε-closure({X})，终态是含有原终态Y的子集，不难看出，这个DFA M与M’等价对于每个NFA M存在一个DFA M ’ ，使得 L(M)=L(M’)，NFA和DFA等价

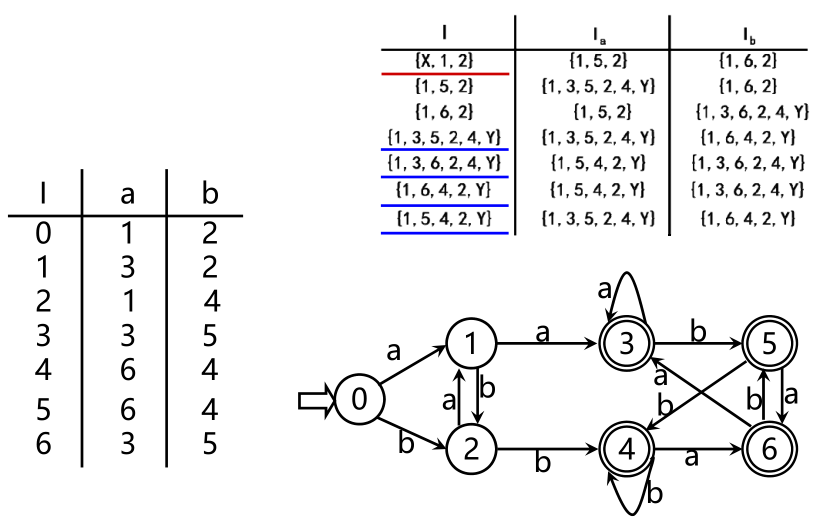
确定有限自动机的化简

对于给定的DFA M，寻找一个状态数比M少的DFAM’，使得L(M)=L(M’)，假设s和t为M的两个状态，称s和t等价：如果从状态s出发能读出某个字α而停止于终态，那么同样，从t出发也能读出α而停止于终，两个状态不等价，则称它们是可区别的态；反之亦然

基本思想

把M的状态集划分为一些不相交的子集，使得任何两个不同子集的状态是可区别的，而同一子集的任何两个状态是等价的， 最后，让每个子集选出一个代表，同时消去其他状态。

对DFA的状态集合S进行第一次划分，正确的分法是：终态和非终态

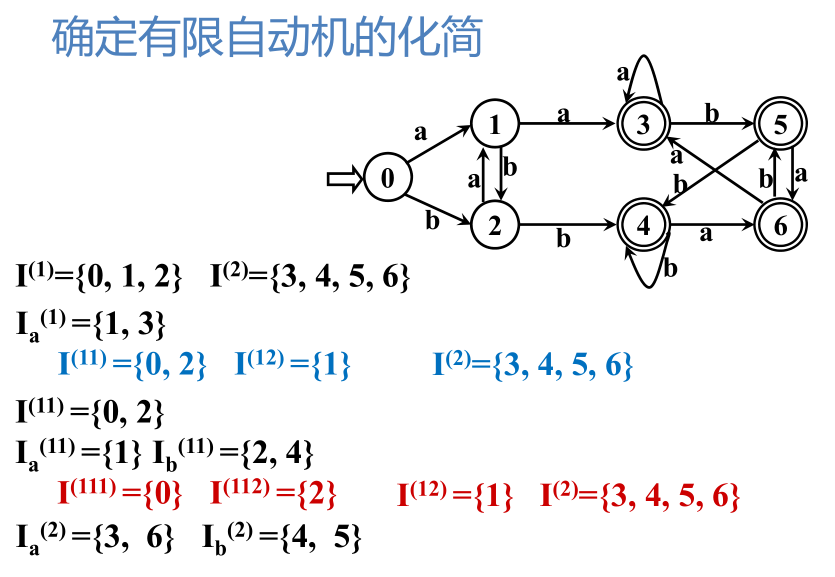
{0} {1} {2} {3, 4, 5, 6}